3 Is 40 Percent Of What
Kalali
Apr 13, 2025 · 5 min read
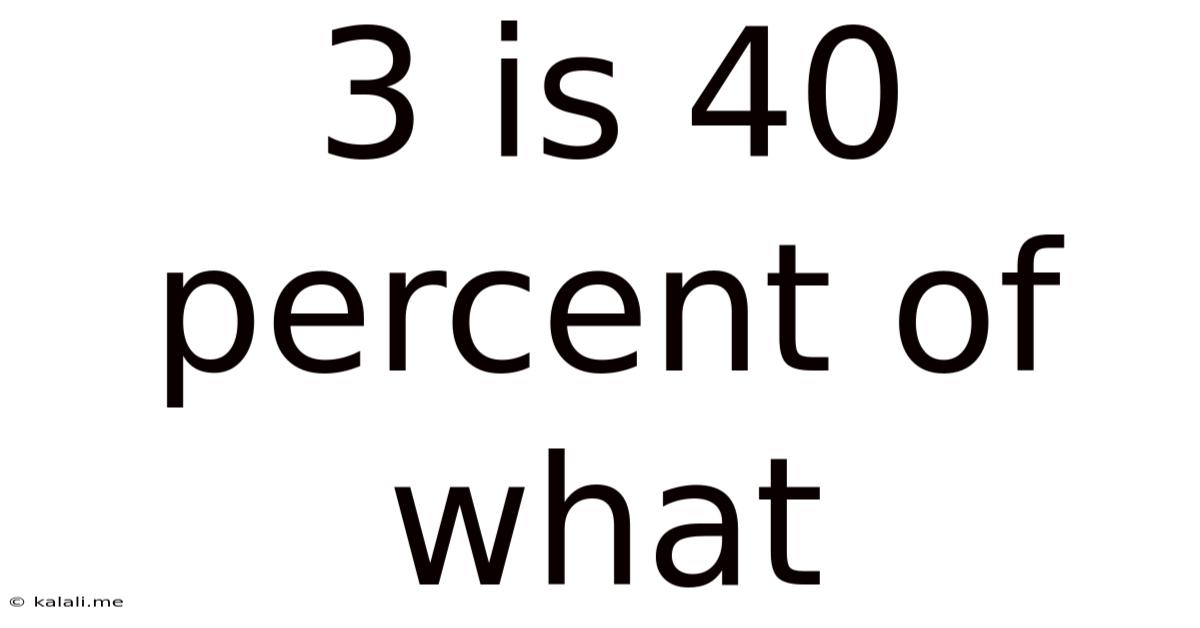
Table of Contents
3 is 40 Percent of What? A Deep Dive into Percentage Calculations and Applications
This seemingly simple question, "3 is 40 percent of what?", opens the door to a broader understanding of percentages, their applications in various fields, and the underlying mathematical principles. While the answer itself is straightforward to calculate, the context and implications of percentage calculations are far-reaching and deserve exploration. This article will not only solve the problem but also delve into the methods, practical applications, and common pitfalls of percentage calculations.
Understanding Percentages: A Foundation
Percentages are a fundamental part of mathematics and are used extensively in everyday life. They represent a proportion or fraction of a whole, expressed as a number out of 100. The symbol "%" denotes percentage. For instance, 50% represents 50 out of 100, which is equivalent to 1/2 or 0.5 in decimal form. Understanding this basic concept is crucial for tackling percentage problems effectively. Mastering percentages helps in various aspects, including:
- Financial Literacy: Calculating discounts, interest rates, taxes, tips, and profit margins.
- Data Analysis: Interpreting statistical data presented as percentages, such as market share, growth rates, and survey results.
- Everyday Calculations: Determining sale prices, understanding nutritional information (e.g., percentage of daily value), and calculating proportions in recipes.
Solving "3 is 40 Percent of What?"
Let's tackle the core question: "3 is 40 percent of what?" This can be solved using several methods. We'll explore two common approaches:
Method 1: Using the Equation
The most straightforward way to solve this is to set up an equation. Let's represent the unknown number as "x". The problem can be written as:
0.40x = 3
To solve for x, we divide both sides of the equation by 0.40:
x = 3 / 0.40
x = 7.5
Therefore, 3 is 40 percent of 7.5.
Method 2: Using Proportions
Another way to solve this is by using proportions. We can set up a proportion where 3 is to x as 40 is to 100:
3/x = 40/100
Cross-multiplying gives us:
40x = 300
Dividing both sides by 40 yields:
x = 300/40
x = 7.5
Again, the answer remains 7.5. Both methods lead to the same result, illustrating the interconnectedness of mathematical concepts.
Practical Applications of Percentage Calculations
The ability to calculate percentages accurately is invaluable in numerous real-world scenarios. Let's explore some examples:
1. Retail Sales and Discounts: Stores frequently offer discounts expressed as percentages. If a shirt is marked down by 20% and the original price is $50, the discount is 0.20 * $50 = $10. The final price is $50 - $10 = $40.
2. Financial Investments: Understanding interest rates is crucial for managing investments. If you invest $1000 at an annual interest rate of 5%, you'll earn $50 in interest after one year (0.05 * $1000 = $50). Compound interest calculations, which involve percentage calculations over multiple periods, are even more complex but equally important.
3. Taxes and Tax Rates: Calculating taxes often involves percentages. A sales tax of 6% on a $100 purchase would be $6 (0.06 * $100 = $6). Income tax calculations are significantly more intricate, but they are fundamentally based on percentage calculations.
4. Statistical Analysis: Percentages are essential in interpreting statistical data. For example, if a survey shows that 75% of respondents prefer a particular brand, this indicates a strong preference. Analyzing data involving percentages allows for informed decision-making in various fields, from marketing to healthcare.
5. Scientific and Engineering Calculations: Percentage calculations are also applied in science and engineering, such as in determining the efficiency of a machine, calculating the concentration of a solution, or expressing experimental error.
Common Pitfalls and Mistakes in Percentage Calculations
While percentage calculations are fundamental, certain common mistakes can lead to inaccurate results. It's crucial to be aware of these potential pitfalls:
-
Confusing Percentage Change with Percentage Points: A change from 20% to 30% is a 50% increase (a 10 percentage point increase is equal to a 50% increase on the base value), not a 10% increase.
-
Incorrect Order of Operations: When dealing with multiple operations (addition, subtraction, multiplication, division), it's vital to follow the order of operations (PEMDAS/BODMAS).
-
Rounding Errors: Rounding intermediate results can accumulate errors, leading to inaccuracies in the final answer. It's best to avoid rounding until the final calculation.
-
Incorrect Percentage-to-Decimal Conversion: Remember to convert percentages to decimals correctly. 25% is equal to 0.25, not 25.
-
Not Considering the Base Value: The base value (the number the percentage is based on) is crucial. Failing to identify the correct base value can lead to significant errors.
Advanced Percentage Calculations and Applications
Beyond the basic calculations, several more advanced techniques and applications exist. These include:
-
Compound Interest: This involves calculating interest on both the principal amount and accumulated interest. The formula for compound interest considers the principal, rate, time, and number of compounding periods.
-
Percentage Increase/Decrease: These calculations determine the percentage change between two values. The formula involves finding the difference between two values and expressing it as a percentage of the original value.
-
Percentage Points vs. Percentage Change: As mentioned earlier, understanding the distinction is crucial for accurate interpretation.
-
Weighted Averages: These involve calculating an average where different values are assigned different weights (percentages).
-
Statistical Significance Testing: Percentage calculations are integral in statistical tests that determine the probability of obtaining a specific result.
Conclusion
The seemingly simple question, "3 is 40 percent of what?", provides a springboard for a deeper dive into the world of percentages. From basic calculations to complex financial modeling, percentages are pervasive in everyday life and various fields. Mastering percentage calculations, understanding their applications, and being aware of potential pitfalls are essential for accurate and effective problem-solving and informed decision-making. By understanding the underlying principles and employing correct methods, you can confidently tackle percentage problems and confidently apply this knowledge to real-world situations. Remember that practice is key – the more you engage with percentage problems, the more proficient you will become.
Latest Posts
Latest Posts
-
What Percent Is 1 Out Of 7
Apr 15, 2025
-
Cuanto Es 60 Mm En Pulgadas
Apr 15, 2025
-
How Many Molecules Are In 0 500 Moles Of H2
Apr 15, 2025
-
What Is 7 16 In A Decimal
Apr 15, 2025
-
5 Is What Percent Of 25
Apr 15, 2025
Related Post
Thank you for visiting our website which covers about 3 Is 40 Percent Of What . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.