21 Is What Percent Of 50
Kalali
Apr 17, 2025 · 5 min read
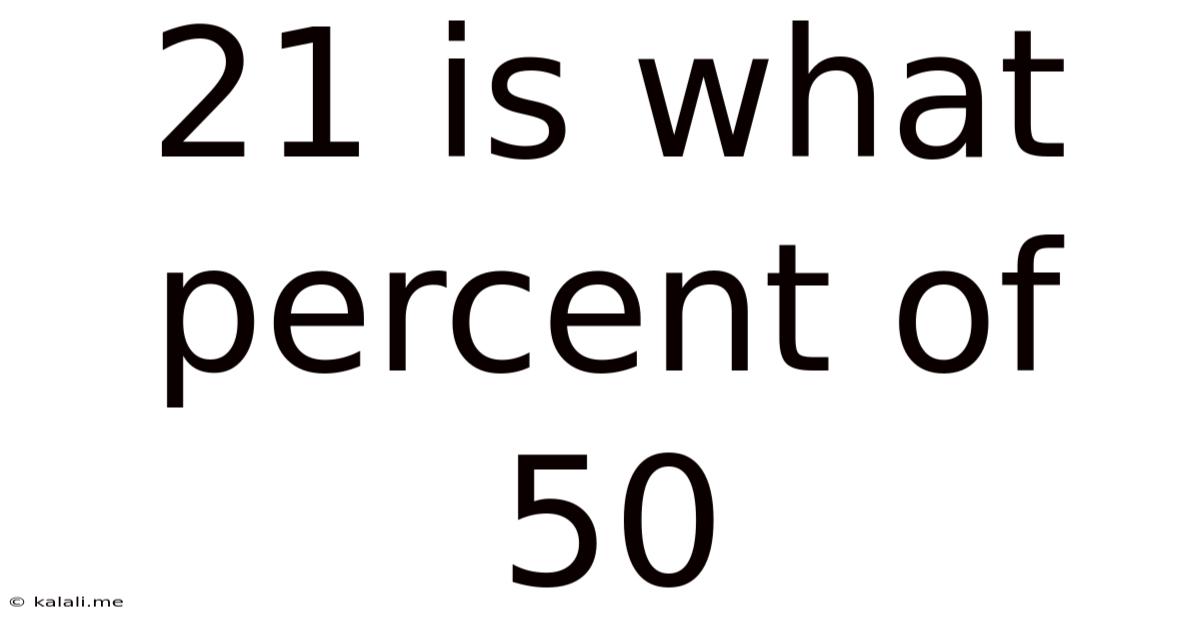
Table of Contents
21 is What Percent of 50? A Comprehensive Guide to Percentage Calculations
This seemingly simple question, "21 is what percent of 50?", opens the door to a broader understanding of percentage calculations, a crucial skill in various aspects of life, from everyday budgeting and shopping to advanced statistical analysis and financial modeling. This article will delve deep into solving this specific problem and then explore the underlying principles and practical applications of percentages. Understanding percentages is fundamental for anyone aiming to improve their numeracy skills and make informed decisions in various contexts.
What is a Percentage?
Before we tackle the problem, let's define what a percentage actually is. A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred" (per centum in Latin). So, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5. Percentages are a convenient way to represent proportions and make comparisons, especially when dealing with different quantities.
Solving "21 is What Percent of 50?"
There are several ways to solve this problem. We'll explore the most common methods, highlighting their strengths and weaknesses:
Method 1: Using Proportions
This method uses the fundamental concept of ratios and proportions. We can set up a proportion:
21/50 = x/100
Where 'x' represents the percentage we're trying to find. To solve for x, we cross-multiply:
21 * 100 = 50 * x
2100 = 50x
x = 2100 / 50
x = 42
Therefore, 21 is 42% of 50.
Method 2: Using Decimal Conversion
This method involves converting the fraction to a decimal and then multiplying by 100 to express it as a percentage.
First, we express 21 as a fraction of 50:
21/50
Next, we convert this fraction to a decimal by dividing 21 by 50:
21 ÷ 50 = 0.42
Finally, we multiply the decimal by 100 to get the percentage:
0.42 * 100 = 42%
Thus, we again arrive at the answer: 21 is 42% of 50.
Method 3: Using the Percentage Formula
The general formula for calculating percentages is:
(Part / Whole) * 100 = Percentage
In our case:
Part = 21 Whole = 50
So the calculation becomes:
(21 / 50) * 100 = 42%
This formula provides a direct and efficient way to solve percentage problems.
Practical Applications of Percentage Calculations
The ability to calculate percentages is invaluable in a multitude of situations. Here are some examples:
-
Calculating Discounts: If a store offers a 20% discount on a $100 item, you can quickly calculate the discount amount and the final price using percentage calculations.
-
Determining Tax Amounts: Understanding sales tax percentages allows you to easily calculate the total cost of a purchase, including taxes.
-
Analyzing Financial Statements: Financial statements rely heavily on percentages to represent ratios, margins, and growth rates. Analyzing these percentages is crucial for making informed financial decisions.
-
Understanding Statistics: Percentages are widely used in statistics to represent proportions, probabilities, and changes in data.
-
Calculating Grades: Many academic grading systems use percentages to represent a student's performance relative to the total possible points.
-
Tracking Progress Towards Goals: Percentages can help track progress towards goals, whether it's weight loss, saving money, or completing a project.
Beyond the Basics: More Complex Percentage Problems
While the problem "21 is what percent of 50?" is relatively straightforward, percentage calculations can become more complex. Here are some examples of more challenging scenarios:
-
Finding the Whole: If 30% of a number is 60, what is the number? This requires working backward from the percentage to find the original whole.
-
Calculating Percentage Increase or Decrease: Determining the percentage change between two values requires subtracting the initial value from the final value, dividing the result by the initial value, and multiplying by 100.
-
Compounding Percentages: When dealing with compound interest or growth rates, percentages are applied repeatedly over time. This necessitates understanding exponential growth.
-
Percentage Points vs. Percentages: A crucial distinction is made between percentage points and percentages. A change from 10% to 20% is a 10 percentage point increase, but a 100% increase (because 10 increased by 100% is 20).
Mastering Percentage Calculations: Tips and Strategies
To master percentage calculations, consider these strategies:
-
Practice Regularly: The more you practice, the more comfortable you'll become with different types of percentage problems.
-
Use Multiple Methods: Trying different approaches helps develop a deeper understanding of the underlying concepts.
-
Utilize Online Calculators (for Verification): Online calculators can be a valuable tool for verifying your answers and building confidence. However, avoid over-reliance; focus on understanding the methodology.
-
Break Down Complex Problems: Complex percentage problems often can be broken down into smaller, manageable steps.
-
Visual Aids: Diagrams or charts can help visualize the problem and make it easier to understand.
-
Understand the Context: The context of a problem is crucial; understanding what the numbers represent will help you apply the correct formula and interpret the results.
Conclusion:
Understanding percentage calculations is a valuable skill applicable in numerous situations. The seemingly simple question, "21 is what percent of 50?", serves as a gateway to mastering this essential skill. By understanding the different methods, practicing regularly, and applying the concepts to real-world scenarios, you can confidently tackle various percentage problems and enhance your numerical literacy. Remember to always check your work and consider using multiple methods to confirm your answers. With consistent effort, you can confidently navigate the world of percentages and utilize this knowledge for informed decision-making.
Latest Posts
Latest Posts
-
What Is The Percentage Of 30
Apr 19, 2025
-
What Are The Agents Of Erosion
Apr 19, 2025
-
How Many Cups Is 16 9 Oz Of Water
Apr 19, 2025
-
What Percentage Is 18 Of 24
Apr 19, 2025
-
How Hot Is 90 Degrees Celsius
Apr 19, 2025
Related Post
Thank you for visiting our website which covers about 21 Is What Percent Of 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.