22 Out Of 24 As A Percentage
Kalali
Apr 17, 2025 · 6 min read
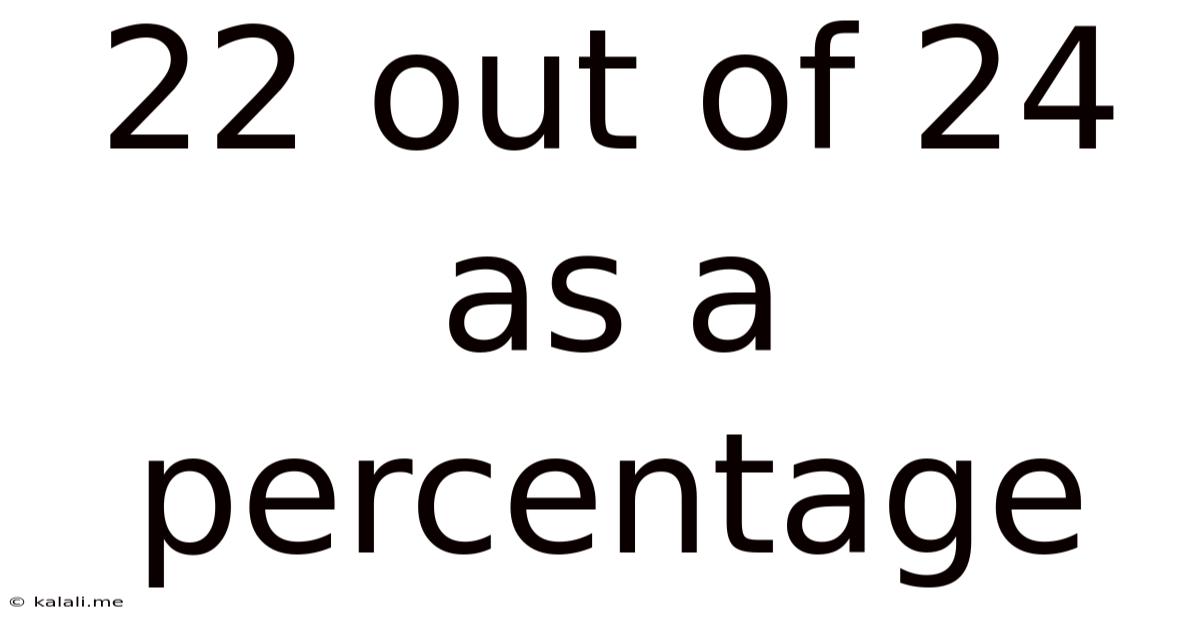
Table of Contents
22 out of 24 as a Percentage: A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in various aspects of life, from calculating grades and discounts to analyzing financial data and understanding statistical information. This article delves deep into the calculation of "22 out of 24 as a percentage," explaining the process step-by-step, exploring different methods, and providing practical applications to solidify your understanding. We'll also cover related percentage problems and discuss how to improve your skills in percentage calculations. This comprehensive guide will empower you to confidently tackle any percentage problem you encounter.
Meta Description: Learn how to calculate 22 out of 24 as a percentage. This comprehensive guide provides step-by-step instructions, explores different methods, and offers practical applications, equipping you with the skills to master percentage calculations.
Understanding the Fundamentals of Percentages
Before diving into the specific calculation of 22 out of 24, let's review the basic concepts of percentages. A percentage is a fraction or a ratio expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For instance, 50% means 50 out of 100, which is equivalent to ½ or 0.5.
Percentages are used to express proportions, rates, or changes. For example, a 10% increase in sales means that sales have increased by 10 units for every 100 units previously sold. Understanding percentages is crucial in many fields, including finance, statistics, and everyday life.
Calculating 22 out of 24 as a Percentage: The Basic Method
The most straightforward method for calculating 22 out of 24 as a percentage involves three simple steps:
-
Convert the fraction: Express "22 out of 24" as a fraction: 22/24.
-
Convert the fraction to a decimal: Divide the numerator (22) by the denominator (24): 22 ÷ 24 = 0.916666... (This decimal is recurring, meaning it goes on infinitely.)
-
Convert the decimal to a percentage: Multiply the decimal by 100: 0.916666... × 100 = 91.6666...%
Therefore, 22 out of 24 is approximately 91.67%. We usually round percentages to two decimal places for practicality.
Alternative Calculation Methods
While the basic method is efficient, let's explore alternative approaches to reinforce your understanding and demonstrate the flexibility of percentage calculations:
-
Simplifying the Fraction: Before converting to a decimal, you can simplify the fraction 22/24 by dividing both the numerator and the denominator by their greatest common divisor (GCD), which is 2. This simplifies the fraction to 11/12. Then, you can divide 11 by 12 to get the decimal (0.916666...), and multiply by 100 to obtain the percentage. This method reduces the complexity of the division.
-
Using Proportions: You can set up a proportion: 22/24 = x/100. Solving for x will give you the percentage. Cross-multiplying yields 24x = 2200, and dividing both sides by 24 gives x ≈ 91.67. This method demonstrates the relationship between fractions and percentages in a more visual way.
-
Using a Calculator: Most calculators have a percentage function. Simply enter 22 ÷ 24 and then press the percentage button (%) to get the result directly. This is the quickest method for obtaining the answer.
Practical Applications of Percentage Calculations
The ability to calculate percentages is invaluable in numerous real-world situations. Here are some examples:
-
Academic Performance: If a student answers 22 out of 24 questions correctly on a test, their score is approximately 91.67%. This helps assess their understanding of the subject matter.
-
Sales and Discounts: If a store offers a 25% discount on an item, you can use percentage calculations to determine the final price after the discount is applied. For example, a $100 item with a 25% discount will cost $75.
-
Financial Analysis: Percentage calculations are extensively used in finance to analyze investment returns, calculate interest rates, and track financial performance. For instance, the calculation of compound interest relies heavily on percentages.
-
Statistical Analysis: Percentages are crucial in presenting and interpreting statistical data, such as population growth rates, survey results, and market share analysis.
-
Everyday Budgeting: Budgeting often involves calculating percentages to allocate funds for different expenses such as rent, food, transportation, and entertainment.
Improving Your Percentage Calculation Skills
Mastering percentage calculations involves consistent practice and understanding the underlying concepts. Here are some tips to improve your skills:
-
Practice Regularly: Solve a variety of percentage problems to build familiarity and confidence. Start with simple examples and gradually progress to more complex ones.
-
Understand the Concepts: Make sure you have a solid grasp of fractions, decimals, and their relationships with percentages.
-
Use Different Methods: Explore different methods of calculation to find the approach that suits you best.
-
Utilize Online Resources: Many online resources, including educational websites and calculators, can help you learn and practice percentage calculations.
-
Real-World Application: Apply percentage calculations to real-life situations to reinforce your understanding and see their practical relevance.
Handling More Complex Percentage Problems
The calculation of 22 out of 24 is a relatively straightforward example. Let's consider some slightly more complex scenarios that build upon the fundamental understanding:
-
Calculating Percentage Increase or Decrease: Imagine a product's price increased from $50 to $60. To calculate the percentage increase, find the difference ($10), divide it by the original price ($50), and multiply by 100: (10/50) * 100 = 20%.
-
Finding the Original Value: Suppose you received a 15% discount on an item and paid $85. To find the original price, let x be the original price. Then, 0.85x = 85. Solving for x gives x = 100. The original price was $100.
-
Working with Multiple Percentages: Consider a scenario where you apply multiple discounts sequentially. For instance, a 20% discount followed by a 10% discount on an item does not equal a 30% discount. The calculations must be performed sequentially.
-
Percentage Points vs. Percentages: Remember that percentage points and percentages are not interchangeable. A change from 20% to 25% is a 5 percentage point increase, but a 25% increase from 20% would be a 5% increase (5/20 * 100 = 25%).
Conclusion: Mastering Percentage Calculations for Success
Understanding and calculating percentages is a valuable skill with far-reaching applications. The ability to confidently convert fractions and decimals to percentages, and vice-versa, is essential for success in various fields. Through consistent practice and application of different methods, you can enhance your proficiency in percentage calculations and apply this knowledge effectively in your personal and professional life. Remember to always double-check your work and choose the method that best suits your understanding and the complexity of the problem. Mastering percentages will empower you to approach various quantitative tasks with greater confidence and accuracy. The example of calculating 22 out of 24 as a percentage serves as a solid foundation for tackling more complex scenarios and ultimately achieving mastery in percentage calculations.
Latest Posts
Latest Posts
-
How Many Cups Is 16 9 Oz Of Water
Apr 19, 2025
-
What Percentage Is 18 Of 24
Apr 19, 2025
-
How Hot Is 90 Degrees Celsius
Apr 19, 2025
-
Cuanto Es 18 Libras En Kilos
Apr 19, 2025
-
24 Oz Is How Many Milliliters
Apr 19, 2025
Related Post
Thank you for visiting our website which covers about 22 Out Of 24 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.