23 Out Of 35 As A Percentage
Kalali
Apr 26, 2025 · 5 min read
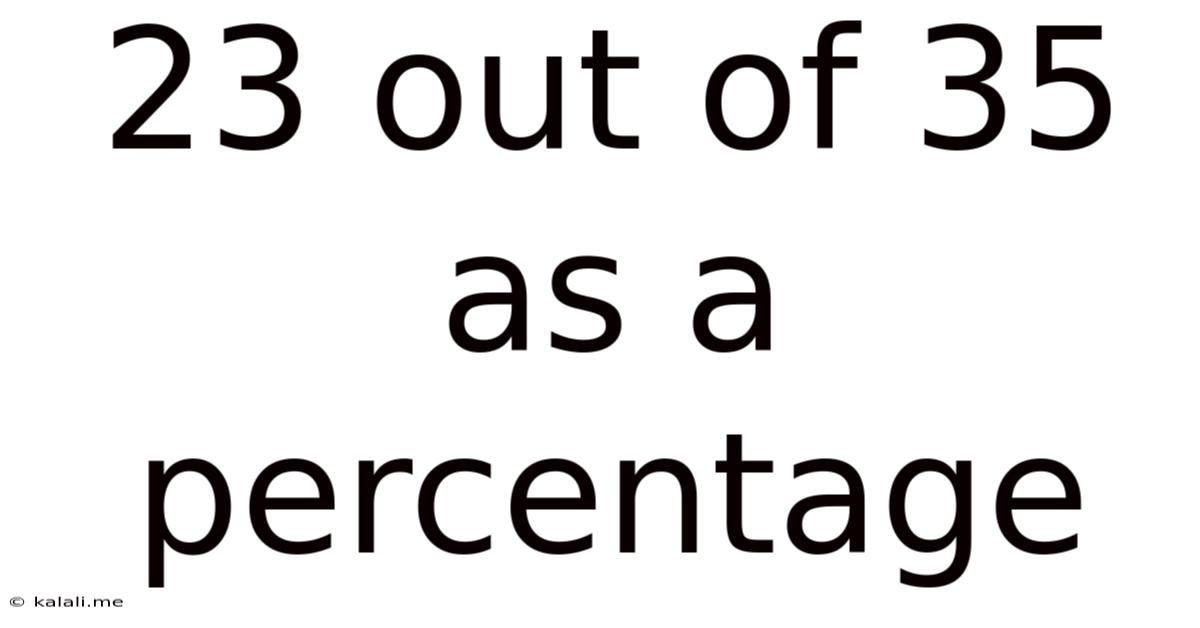
Table of Contents
23 out of 35 as a Percentage: A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across numerous fields, from finance and statistics to everyday life. This article dives deep into calculating percentages, specifically addressing the question: what is 23 out of 35 as a percentage? We'll not only provide the answer but also explore the underlying principles, various calculation methods, and practical applications to solidify your understanding. This guide is designed for anyone seeking a comprehensive understanding of percentage calculations, regardless of their mathematical background.
What is a Percentage?
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "out of one hundred" (per centum in Latin). Percentages are a convenient and widely used way to represent proportions, ratios, and rates of change. They provide a standardized method for comparing different quantities and making sense of data.
Calculating 23 out of 35 as a Percentage: The Basic Method
The most straightforward method involves converting the fraction 23/35 into a percentage. Here's how:
-
Form a Fraction: Express the problem as a fraction: 23/35. This represents 23 parts out of a total of 35 parts.
-
Convert to Decimal: Divide the numerator (23) by the denominator (35): 23 ÷ 35 ≈ 0.657
-
Convert to Percentage: Multiply the decimal by 100: 0.657 × 100 = 65.7%
Therefore, 23 out of 35 is approximately 65.7%.
Alternative Methods for Calculating Percentages
While the above method is the most common, alternative approaches offer flexibility depending on the context and available tools.
-
Using a Calculator: Most calculators have a percentage function (%) that simplifies the process. Simply enter 23 ÷ 35 and then press the % button. The result will directly display as 65.7%.
-
Using Proportions: Set up a proportion: 23/35 = x/100. Cross-multiply and solve for x: 35x = 2300; x = 2300/35 ≈ 65.7. This method highlights the proportional relationship between the fraction and the percentage.
-
Using Spreadsheet Software: Spreadsheet programs like Microsoft Excel or Google Sheets provide built-in functions for percentage calculations. The formula
=23/35*100will directly yield the percentage. This is especially useful for handling large datasets or complex percentage calculations.
Understanding the Result: What Does 65.7% Mean?
The result, 65.7%, signifies that 23 represents approximately 65.7% of the total value of 35. This means that if you divide 35 into 100 equal parts, 23 would occupy 65.7 of those parts. Understanding this context is crucial in interpreting percentage calculations in various scenarios.
Applications of Percentage Calculations in Real-World Scenarios
Percentage calculations find applications across a wide range of fields:
-
Academic Performance: Calculating grades, test scores, and overall academic performance often involves percentages. For instance, a student scoring 23 out of 35 on a quiz achieved a grade of 65.7%.
-
Financial Calculations: Percentages are fundamental in finance, used for calculating interest rates, discounts, taxes, profit margins, and investment returns. Understanding percentage change is crucial for tracking financial performance.
-
Statistics and Data Analysis: Percentages are extensively used to represent proportions and probabilities in statistical analysis. They provide a concise way to summarize and present data, enabling easier comparison and interpretation.
-
Sales and Marketing: Businesses rely on percentages to track sales figures, conversion rates, market share, and customer satisfaction. Understanding these percentages helps companies make informed decisions about their strategies.
-
Everyday Life: From calculating tips in restaurants to understanding discounts in stores, percentages are an integral part of daily life. Being proficient in percentage calculations empowers you to make informed decisions and navigate everyday financial situations.
Rounding Percentages: Precision and Practicality
In many practical applications, rounding percentages to a certain level of precision is necessary. For example, instead of 65.7%, you might round it to 66% for simplicity. However, the level of precision required depends on the context. In financial calculations, higher precision is often necessary, while in informal settings, rounding to the nearest whole number may suffice.
Beyond the Basics: Advanced Percentage Calculations
While the calculation of 23 out of 35 is a straightforward example, percentages can be used in more complex scenarios:
-
Percentage Increase/Decrease: Calculating the percentage change between two values involves determining the difference, dividing by the original value, and multiplying by 100. This is crucial for tracking growth or decline in various metrics. For instance, if a value increases from 35 to 45, the percentage increase is calculated as: (45-35)/35 * 100 ≈ 28.6%.
-
Percentage of a Percentage: Calculating a percentage of a percentage involves multiplying the two percentages. For example, finding 10% of 20% is calculated as 0.10 * 0.20 = 0.02 or 2%.
-
Compound Interest: Compound interest calculations involve repeatedly applying a percentage increase to a principal amount over time. This is a common application in finance and investment calculations.
Mastering Percentage Calculations: Tips and Practice
Mastering percentage calculations involves consistent practice and understanding the underlying concepts. Here are some tips to improve your skills:
-
Practice Regularly: Solve various percentage problems to build your confidence and familiarity with the calculations.
-
Understand the Concepts: Ensure you have a solid grasp of fractions, decimals, and their relationship to percentages.
-
Use Different Methods: Experiment with different calculation methods (manual calculation, calculator, spreadsheet software) to find the approach that suits you best.
-
Check Your Answers: Always double-check your calculations to ensure accuracy.
-
Apply to Real-World Scenarios: Use percentage calculations in real-life situations to reinforce your understanding and improve your practical skills.
Conclusion:
Calculating 23 out of 35 as a percentage, resulting in approximately 65.7%, is a fundamental percentage calculation. Understanding this process and its applications extends beyond a simple mathematical problem; it's a crucial skill for navigating various aspects of life, from academic pursuits and financial management to everyday decision-making. By mastering percentage calculations and understanding their diverse applications, you equip yourself with a valuable tool for interpreting data, making informed decisions, and solving problems across numerous domains. Remember to practice regularly and apply your knowledge to real-world scenarios to solidify your understanding and become proficient in the art of percentage calculations.
Latest Posts
Latest Posts
-
What Are The Characteristics Of Metals
Apr 27, 2025
-
Cuantos Son 10 Metros En Pies
Apr 27, 2025
-
What Is The Least Common Multiple Of 3 2
Apr 27, 2025
-
What Is The Input Of Photosynthesis
Apr 27, 2025
-
8 Is What Percent Of 60
Apr 27, 2025
Related Post
Thank you for visiting our website which covers about 23 Out Of 35 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.