24 Is What Percent Of 20
Kalali
Apr 16, 2025 · 5 min read
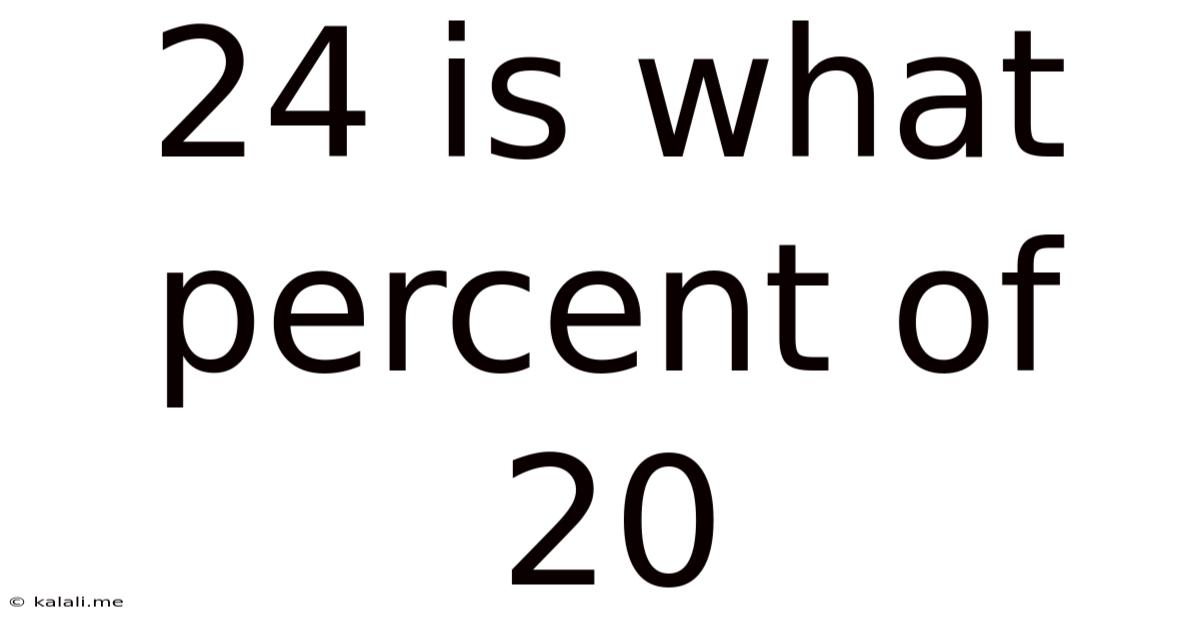
Table of Contents
24 is What Percent of 20? A Deep Dive into Percentage Calculations and Their Applications
Meta Description: Learn how to calculate percentages, understand the concept of ratios, and explore real-world applications of percentage calculations using the example: "24 is what percent of 20?" This comprehensive guide covers various methods and provides practical examples.
Finding what percentage 24 represents of 20 might seem like a simple arithmetic problem, but it unlocks a deeper understanding of percentages, ratios, and their widespread applications in various fields. This article will not only provide the solution but will also delve into the underlying concepts, explore different calculation methods, and showcase the practical relevance of percentage calculations in everyday life and professional contexts.
Understanding Percentages and Ratios
Before diving into the calculation, let's solidify our understanding of percentages and ratios. A percentage is a way of expressing a number as a fraction of 100. The symbol "%" represents "per cent" or "out of 100". A ratio, on the other hand, is a comparison of two quantities. It shows the relative size of one quantity compared to another. Percentages and ratios are intrinsically linked; a percentage can be expressed as a ratio, and vice versa.
For example, 50% can be expressed as the ratio 50:100 or its simplified form 1:2. This means that for every 2 parts, 1 part is 50%. This relationship is crucial for understanding percentage calculations. In our problem, "24 is what percent of 20?", we are essentially looking for the ratio of 24 to 20, expressed as a percentage.
Method 1: Using the Percentage Formula
The most straightforward way to solve "24 is what percent of 20?" is using the basic percentage formula:
(Part / Whole) * 100% = Percentage
In this case:
- Part: 24 (the number we want to express as a percentage)
- Whole: 20 (the total or base number)
Substituting the values into the formula:
(24 / 20) * 100% = 120%
Therefore, 24 is 120% of 20. This result indicates that 24 is larger than 20.
Method 2: Setting up a Proportion
Another effective method is setting up a proportion. A proportion is an equation stating that two ratios are equal. We can set up the proportion as follows:
x/100 = 24/20
Where 'x' represents the percentage we need to find. To solve for x, we can cross-multiply:
20x = 2400
x = 2400 / 20
x = 120
Therefore, 24 is 120% of 20. This method offers a visual representation of the ratio relationship.
Method 3: Using Decimal Conversion
This method involves converting the ratio into a decimal and then multiplying by 100%.
First, we divide the part by the whole:
24 / 20 = 1.2
Then, we multiply the decimal by 100% to express it as a percentage:
1.2 * 100% = 120%
Thus, 24 is 120% of 20. This approach is particularly useful when dealing with more complex percentage calculations.
Understanding the Result: Percentages Greater than 100%
The result of 120% might initially seem counterintuitive. Percentages are often perceived as being limited to the range of 0% to 100%. However, percentages greater than 100% simply indicate that the "part" is larger than the "whole." In our example, 24 exceeds 20, hence the percentage is greater than 100%. This concept is frequently encountered when dealing with growth rates, increases, or comparisons where one value surpasses another.
Real-World Applications of Percentage Calculations
Percentage calculations are ubiquitous in various aspects of life. Here are some examples:
-
Finance: Calculating interest rates, discounts, tax amounts, profit margins, and investment returns all rely on percentage calculations. For instance, understanding how much interest you'll earn on a savings account or how much you'll save with a discount requires precise percentage computations.
-
Business: Analyzing sales figures, market share, growth rates, and cost analysis are all dependent on calculating percentages. Business decisions often hinge on interpreting data expressed as percentages, like comparing sales figures from year to year or tracking the success of a marketing campaign.
-
Science and Statistics: Percentages are fundamental in representing data and probabilities. Statistical analysis relies heavily on expressing data as percentages to understand trends and draw meaningful conclusions. For example, presenting survey results, expressing experimental errors, or describing the probability of an event all use percentages effectively.
-
Everyday Life: Calculating tips, determining sale prices, understanding nutritional information on food labels, and even figuring out the percentage of a task completed are all common applications of percentage calculations in daily life.
-
Education: Grading systems, performance assessments, and test scores are frequently expressed as percentages, providing a standardized method for evaluating student progress.
Advanced Percentage Problems and Considerations
While the problem "24 is what percent of 20?" provides a foundational understanding, more complex percentage problems exist. These often involve:
- Multiple percentage changes: Calculating the overall percentage change after multiple successive increases or decreases.
- Percentage increase/decrease: Finding the percentage increase or decrease between two values.
- Percentage points: Understanding the difference between percentage change and percentage points. Percentage points represent the absolute difference between two percentages, whereas percentage change represents the relative difference.
Conclusion
This in-depth exploration of "24 is what percent of 20?" has expanded beyond a simple arithmetic problem. We've delved into the core concepts of percentages and ratios, explored different calculation methods, and highlighted the vast practical applications of percentage calculations across various domains. Understanding percentage calculations is not merely an academic exercise; it's a vital skill applicable to diverse aspects of life, from managing personal finances to making informed business decisions and analyzing scientific data. Mastering these calculations empowers you to interpret information more effectively, make better decisions, and navigate a world saturated with data expressed in percentages. Remember, the key is understanding the underlying concepts and applying the appropriate method to solve the problem at hand. The ability to confidently solve percentage problems, even those seemingly simple at first glance, opens doors to deeper understanding and practical applications in numerous fields.
Latest Posts
Latest Posts
-
18 5 As A Mixed Number
Apr 19, 2025
-
What Is The Prefix Of In
Apr 19, 2025
-
The Ability Of A Substance To Catch Fire Or Burn
Apr 19, 2025
-
35 8 As A Mixed Number
Apr 19, 2025
-
What Is The Domain Of The Function Graphed Below
Apr 19, 2025
Related Post
Thank you for visiting our website which covers about 24 Is What Percent Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.