27 10 As A Mixed Number
Kalali
Apr 11, 2025 · 5 min read
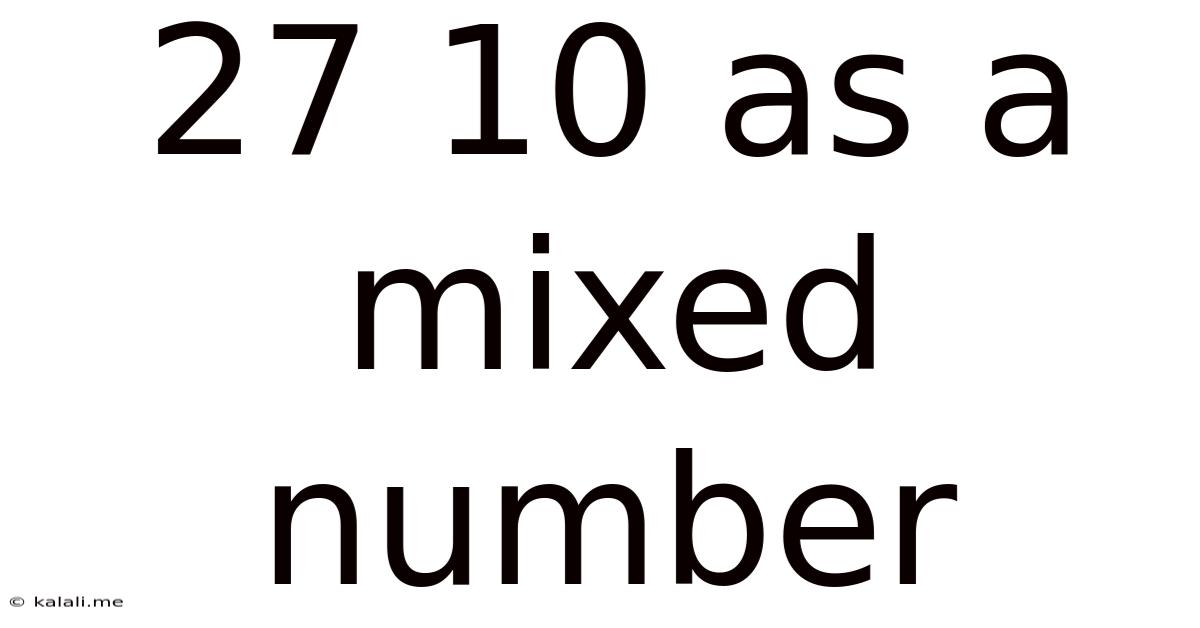
Table of Contents
27/10 as a Mixed Number: A Comprehensive Guide
Understanding fractions and their conversions is fundamental to mathematics. This article delves deep into the conversion of the improper fraction 27/10 into a mixed number, explaining the process step-by-step, providing examples, and exploring related concepts. We'll cover not just the mechanics of the conversion but also the underlying mathematical principles, ensuring a thorough understanding for all readers.
What is a Mixed Number?
Before diving into the conversion, let's define what a mixed number is. A mixed number is a combination of a whole number and a proper fraction. A proper fraction is one where the numerator (the top number) is smaller than the denominator (the bottom number). For example, 2 ¾ is a mixed number, where 2 is the whole number and ¾ is the proper fraction. Mixed numbers are a useful way to represent quantities that are greater than one but not a whole number.
Converting Improper Fractions to Mixed Numbers
An improper fraction is a fraction where the numerator is greater than or equal to the denominator. 27/10 is an improper fraction because 27 (the numerator) is greater than 10 (the denominator). To convert an improper fraction to a mixed number, we need to divide the numerator by the denominator.
Step-by-Step Conversion of 27/10
-
Divide the numerator by the denominator: We divide 27 by 10. This gives us a quotient of 2 and a remainder of 7.
-
The quotient becomes the whole number: The quotient, 2, becomes the whole number part of our mixed number.
-
The remainder becomes the numerator of the proper fraction: The remainder, 7, becomes the numerator of the proper fraction.
-
The denominator remains the same: The denominator remains 10.
-
Combine the whole number and the proper fraction: Therefore, 27/10 as a mixed number is 2 ⁷/₁₀.
Visualizing the Conversion
Imagine you have 27 slices of pizza, and each pizza has 10 slices. You can make 2 whole pizzas (20 slices) with 7 slices left over. This leftover 7 slices represents ⁷/₁₀ of a pizza. Thus, you have 2 whole pizzas and ⁷/₁₀ of a pizza, which is represented by the mixed number 2 ⁷/₁₀. This visual representation helps solidify the understanding of the conversion process.
Further Examples of Improper Fraction to Mixed Number Conversion
Let's look at a few more examples to reinforce the concept:
-
17/5: Dividing 17 by 5 gives a quotient of 3 and a remainder of 2. Therefore, 17/5 = 3²/₅
-
22/7: Dividing 22 by 7 gives a quotient of 3 and a remainder of 1. Therefore, 22/7 = 3 ¹/₇
-
31/4: Dividing 31 by 4 gives a quotient of 7 and a remainder of 3. Therefore, 31/4 = 7 ³/₄
These examples showcase the consistent application of the division process to transform improper fractions into their mixed number equivalents.
Converting Mixed Numbers back to Improper Fractions
The reverse process—converting a mixed number back to an improper fraction—is equally important. Let's use our original example, 2 ⁷/₁₀:
-
Multiply the whole number by the denominator: 2 * 10 = 20
-
Add the numerator: 20 + 7 = 27
-
The result becomes the new numerator: 27
-
The denominator remains the same: 10
-
Combine the numerator and denominator: Therefore, 2 ⁷/₁₀ = 27/10
This demonstrates the reciprocal nature of these two conversion processes.
Applications of Mixed Numbers and Improper Fractions
Both mixed numbers and improper fractions serve valuable purposes in various mathematical contexts. Mixed numbers are often preferred for representing quantities in real-world scenarios, as they are more easily understood intuitively. For example, it's easier to visualize 2 ⁷/₁₀ pizzas than 27/10 pizzas. However, improper fractions are often more convenient for performing calculations, particularly multiplication and division of fractions.
Solving Problems Involving Mixed Numbers and Improper Fractions
Let's consider a problem: John baked 2 ⁷/₁₀ pies. He ate ½ a pie. How much pie is left?
-
Convert the mixed number to an improper fraction: 2 ⁷/₁₀ = 27/10
-
Subtract the fraction representing the amount eaten: 27/10 - ½. To subtract, we need a common denominator, which is 10. So, ½ becomes ⁵/₁₀.
-
Subtract the fractions: 27/10 - ⁵/₁₀ = 22/10
-
Simplify the resulting improper fraction (optional): 22/10 simplifies to ¹¹/₅
-
Convert the improper fraction back to a mixed number (optional): ¹¹/₅ = 2 ¹/₅
Therefore, John has 2 ¹/₅ pies left. This example showcases the interplay between mixed numbers and improper fractions in solving practical problems.
Further Exploration of Fraction Concepts
This detailed exploration of converting 27/10 into a mixed number extends beyond a simple conversion exercise. It touches upon fundamental concepts within fractions, including proper fractions, improper fractions, mixed numbers, and the processes of conversion between them. Understanding these concepts is vital for success in various mathematical areas, including algebra, geometry, and calculus. Mastering these foundational concepts will provide a strong basis for tackling more advanced mathematical problems. Furthermore, understanding the visualization of fractions, as illustrated by the pizza example, allows for a stronger intuitive grasp of fractional quantities. This visual representation aids in comprehension and can be especially helpful for learners who benefit from visual aids in their learning process.
Conclusion
Converting 27/10 to the mixed number 2 ⁷/₁₀ involves a simple yet crucial process in mathematics. This article provided a comprehensive guide, going beyond the simple conversion to explore the underlying principles, provide examples, and discuss practical applications. By mastering this conversion, and understanding the broader concepts of fractions, you build a solid mathematical foundation for future learning and problem-solving. Remember, the key lies in understanding the division process, the relationship between the whole number, numerator, and denominator, and the ability to move fluidly between improper fractions and mixed numbers. This understanding empowers you to solve a wide range of problems involving fractions, solidifying your mathematical skills and enhancing your problem-solving abilities.
Latest Posts
Latest Posts
-
3 Gallons Is How Many Cups
Apr 18, 2025
-
Cuanto Son 80 Grados Fahrenheit En Centigrados
Apr 18, 2025
-
Cuanto Es 30 Grados Farenheit En Centigrados
Apr 18, 2025
-
How Much Is Half A Pound In Ounces
Apr 18, 2025
-
What Percent Of 10 Is 6
Apr 18, 2025
Related Post
Thank you for visiting our website which covers about 27 10 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.