29 Out Of 40 As A Percentage
Kalali
Mar 08, 2025 · 5 min read
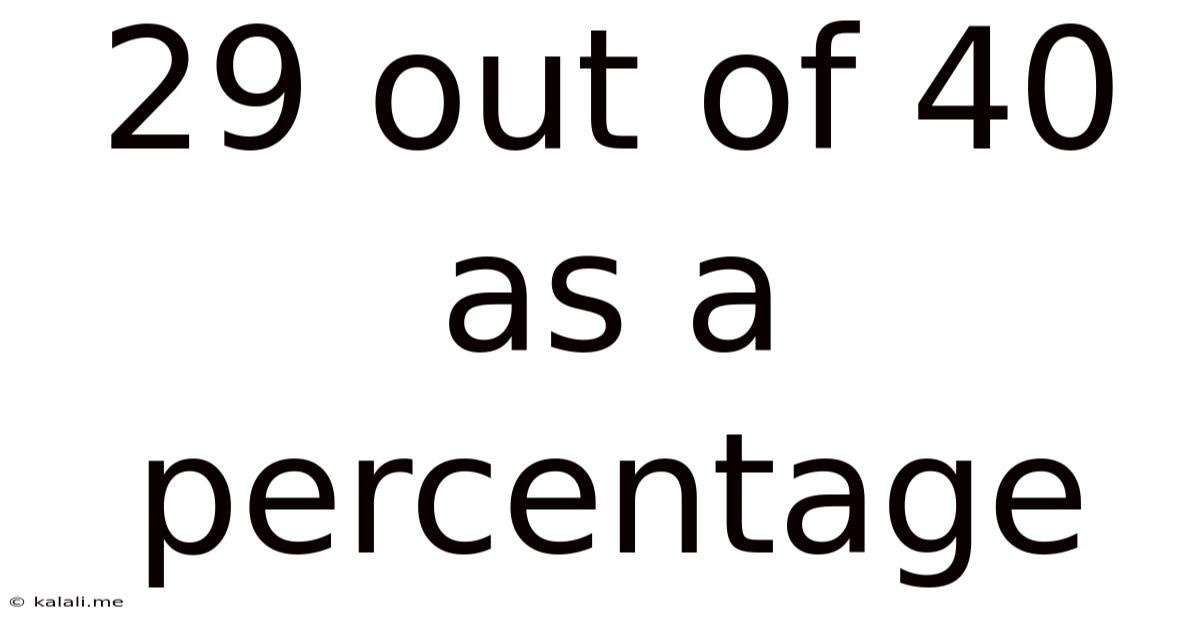
Table of Contents
29 out of 40 as a Percentage: A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill applicable across numerous fields, from academic assessments to financial analysis. Understanding how to convert fractions and ratios into percentages is crucial for interpreting data and making informed decisions. This comprehensive guide will delve into the calculation of 29 out of 40 as a percentage, exploring different methods and providing practical examples to solidify your understanding. We'll also touch upon broader applications of percentage calculations and how to confidently handle similar problems in the future.
Understanding Percentages
Before we dive into the specific calculation, let's establish a clear understanding of what percentages represent. A percentage is simply a fraction or ratio expressed as a number out of 100. The symbol "%" signifies "per cent," meaning "out of one hundred." For instance, 50% means 50 out of 100, which can be simplified to 1/2 or 0.5.
Methods for Calculating 29 out of 40 as a Percentage
There are several approaches to calculating 29 out of 40 as a percentage. Each method offers a slightly different perspective on the underlying mathematical principles.
Method 1: The Fraction Method
This method directly converts the ratio "29 out of 40" into a fraction and then converts that fraction to a percentage.
-
Express as a Fraction: The ratio "29 out of 40" can be written as the fraction 29/40.
-
Convert to a Decimal: To convert the fraction to a decimal, divide the numerator (29) by the denominator (40): 29 ÷ 40 = 0.725
-
Convert to a Percentage: Multiply the decimal by 100 to express it as a percentage: 0.725 x 100 = 72.5%
Therefore, 29 out of 40 is 72.5%.
Method 2: The Proportion Method
This method uses proportions to solve for the unknown percentage.
-
Set up a Proportion: We can set up a proportion: 29/40 = x/100, where 'x' represents the unknown percentage.
-
Cross-Multiply: Cross-multiply the proportion: 29 * 100 = 40 * x
-
Solve for x: This gives us 2900 = 40x. Dividing both sides by 40, we get x = 72.5.
-
Express as a Percentage: Therefore, x = 72.5%, confirming our previous result.
Method 3: Using a Calculator
Most calculators have a percentage function that simplifies this calculation significantly. Simply input 29 ÷ 40 and then multiply the result by 100. The calculator will directly provide the answer: 72.5%.
Practical Applications and Real-World Examples
Understanding percentage calculations is vital in numerous real-world situations:
-
Academic Performance: If a student answers 29 out of 40 questions correctly on a test, their score is 72.5%. This allows for easy comparison of performance across different tests and students.
-
Financial Calculations: Percentage calculations are fundamental in finance, used for calculating interest rates, discounts, profit margins, and tax rates. For example, a 72.5% discount on a product would significantly reduce its price.
-
Data Analysis: In data analysis, percentages help to represent proportions and trends in data sets. For instance, analyzing survey results might reveal that 72.5% of respondents prefer a particular product.
-
Sales and Marketing: Sales figures are often expressed as percentages to show growth or decline over time. A 72.5% conversion rate from leads to sales indicates high effectiveness in marketing strategies.
-
Sports Statistics: Batting averages, field goal percentages, and other sports statistics rely heavily on percentage calculations to evaluate player performance and team success.
Expanding on Percentage Calculations: Beyond 29 out of 40
The principles illustrated above can be applied to any ratio or fraction. To calculate a percentage from any given ratio, follow these steps:
-
Express as a Fraction: Write the ratio as a fraction (part/whole).
-
Convert to a Decimal: Divide the numerator by the denominator.
-
Convert to a Percentage: Multiply the decimal by 100 and add the "%" symbol.
Example: What is 15 out of 25 as a percentage?
-
Fraction: 15/25
-
Decimal: 15 ÷ 25 = 0.6
-
Percentage: 0.6 x 100 = 60%
Dealing with More Complex Scenarios
While the examples above involve straightforward calculations, percentage problems can become more complex. Here are some scenarios and how to handle them:
-
Percentages of Percentages: Calculating a percentage of another percentage requires multiplying the two percentages together. For instance, finding 20% of 50% would involve multiplying 0.20 by 0.50, resulting in 0.10 or 10%.
-
Percentage Increase/Decrease: These calculations involve finding the difference between two values and expressing that difference as a percentage of the original value. For example, if a price increases from $100 to $120, the percentage increase is calculated as [(120 - 100) / 100] * 100 = 20%.
-
Percentage Points vs. Percentage Change: It's crucial to understand the difference between these terms. A percentage point refers to an absolute change in percentage values, while a percentage change refers to the relative change. For example, an increase from 50% to 55% is a 5 percentage point increase, but a 10% percentage change.
Tips for Accurate Percentage Calculations
-
Double-check your work: Always verify your calculations to ensure accuracy.
-
Use a calculator: Calculators can significantly reduce the risk of errors, especially for more complex problems.
-
Understand the context: Pay close attention to the context of the problem to avoid misinterpreting the data.
-
Practice regularly: Consistent practice will solidify your understanding and improve your calculation speed and accuracy.
Conclusion: Mastering Percentage Calculations
Understanding percentage calculations is a crucial life skill. This guide provided a comprehensive overview of how to calculate 29 out of 40 as a percentage, employing various methods and highlighting their practical applications. By understanding the underlying principles and mastering different calculation techniques, you'll be equipped to confidently tackle a wide range of percentage problems in various contexts, boosting your skills in academics, finance, and beyond. Remember that consistent practice is key to mastering this essential skill.
Latest Posts
Latest Posts
-
How Many 16ths Are In An Inch
Jul 10, 2025
-
How Many Cups Are In A Pound Of Rice
Jul 10, 2025
-
How Many Pounds Is One Ton Equal
Jul 10, 2025
-
A Warehouse Received 250 Orders In April
Jul 10, 2025
-
How Many Square Inches Are In 1 Square Foot
Jul 10, 2025
Related Post
Thank you for visiting our website which covers about 29 Out Of 40 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.