3 Of 20 Is What Percent
Kalali
Mar 31, 2025 · 5 min read
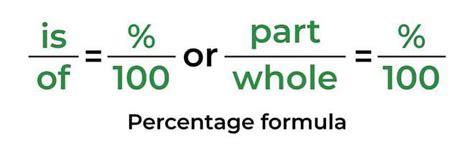
Table of Contents
3 out of 20 is What Percent? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across numerous areas of life, from calculating discounts in a store to interpreting statistical data. This comprehensive guide will not only answer the question, "3 out of 20 is what percent?" but also equip you with the knowledge and tools to tackle any percentage problem with confidence. We'll explore various methods, delve into practical applications, and offer tips for mastering percentage calculations.
Understanding the Basics of Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" itself is derived from the Latin "per centum," meaning "out of a hundred." Therefore, 1% represents one out of a hundred (1/100), 50% represents fifty out of a hundred (50/100 or 1/2), and so on.
This fundamental concept is crucial for understanding how percentages work. It establishes the core relationship between a part and a whole, expressed as a fraction relative to 100. This seemingly simple concept forms the basis of countless calculations in everyday life and complex mathematical analyses.
Calculating "3 out of 20 is What Percent?"
Now, let's address the specific question: What percentage is 3 out of 20? We can use several methods to solve this:
Method 1: Using the Fraction Method
The most straightforward approach involves converting the given numbers into a fraction and then converting that fraction into a percentage.
-
Form a fraction: Represent "3 out of 20" as a fraction: 3/20.
-
Convert to a decimal: Divide the numerator (3) by the denominator (20): 3 ÷ 20 = 0.15
-
Convert to a percentage: Multiply the decimal by 100: 0.15 x 100 = 15%
Therefore, 3 out of 20 is 15%.
Method 2: Using Proportions
Another effective method uses proportions. We can set up a proportion to solve for the unknown percentage:
-
Set up the proportion: 3/20 = x/100 (where 'x' represents the percentage we want to find)
-
Cross-multiply: 20x = 300
-
Solve for x: x = 300/20 = 15
Therefore, 3 out of 20 is 15%. This method highlights the proportional relationship between the part and the whole relative to 100.
Method 3: Using a Calculator
Most calculators have a percentage function that simplifies this process. Simply enter "3 ÷ 20" and then multiply the result by 100. This method offers speed and efficiency, especially when dealing with more complex calculations.
Practical Applications of Percentage Calculations
The ability to calculate percentages extends far beyond simple arithmetic exercises. Understanding percentages is vital in various real-world scenarios, including:
-
Financial calculations: Calculating interest rates, discounts, taxes, profit margins, and investment returns all rely heavily on percentage calculations. For example, determining the final price after a 20% discount requires understanding how to calculate 20% of the original price and subtracting it from the original price.
-
Statistical analysis: Percentages are essential for interpreting data presented in graphs, charts, and tables. For instance, understanding the percentage of respondents who chose a particular option in a survey helps researchers draw meaningful conclusions. Similarly, in data analysis related to business performance, marketing campaigns, or website traffic, understanding percentage change and growth rates is crucial.
-
Scientific measurements: Percentages are commonly used to express concentrations, error rates, and changes in measurements across numerous scientific disciplines. Understanding the percentage composition of a chemical solution, for instance, is critical in various laboratory procedures.
-
Everyday life: From calculating tips in restaurants (e.g., a 15% tip) to understanding sales tax percentages, percentages are integral to numerous everyday activities. Similarly, understanding percentage increases and decreases in prices is essential for budget planning and making informed purchasing decisions.
Beyond Basic Percentage Calculations: Advanced Techniques
While calculating "3 out of 20 is what percent?" is a straightforward example, percentage calculations can become more complex. Understanding advanced techniques can greatly enhance your ability to solve a wider range of percentage-related problems.
Percentage Increase and Decrease
Calculating percentage increases and decreases involves determining the change in a value relative to the original value. The formula for percentage increase is:
[(New Value - Original Value) / Original Value] x 100
Similarly, the formula for percentage decrease is:
[(Original Value - New Value) / Original Value] x 100
For example, if a product's price increases from $10 to $12, the percentage increase is:
[(12 - 10) / 10] x 100 = 20%
Finding the Original Value
Sometimes, you know the percentage change and the new value but need to find the original value. This requires rearranging the percentage increase/decrease formulas.
Working with Compound Percentages
Compound percentages involve calculating percentages on percentages. This is frequently encountered in financial calculations, such as compound interest, where interest earned in one period is added to the principal before calculating the interest for the next period.
Tips and Tricks for Mastering Percentage Calculations
-
Memorize common percentage equivalents: Knowing that 1/4 = 25%, 1/2 = 50%, and 3/4 = 75% can significantly speed up calculations.
-
Use estimation: Before performing precise calculations, estimate the answer to check if your final answer is reasonable. Rounding numbers can also help simplify calculations.
-
Practice regularly: The key to mastering percentage calculations is consistent practice. Work through various problems to reinforce your understanding and build confidence.
-
Utilize online resources: Numerous websites and apps offer practice problems and tutorials on percentage calculations. These resources can provide additional support and guidance.
-
Break down complex problems: When faced with complex percentage problems, break them down into smaller, more manageable steps. This approach simplifies the process and reduces the likelihood of errors.
Conclusion
Understanding percentages is a valuable skill with applications across numerous fields. This comprehensive guide has not only answered the question, "3 out of 20 is what percent?" (15%) but also provided a detailed explanation of various methods, practical applications, and advanced techniques. By mastering these concepts, you can confidently tackle percentage calculations in any situation, improving your problem-solving abilities and enhancing your understanding of numerical data. Remember to practice regularly to solidify your understanding and become proficient in handling percentage calculations.
Latest Posts
Latest Posts
-
Is 0 0000008 J A Little Kinetic Enegy
Apr 01, 2025
-
17 Of 20 Is What Percent
Apr 01, 2025
-
What Is 6 To The Power Of 3
Apr 01, 2025
-
Cual Es El 10 Por Ciento De 1000
Apr 01, 2025
-
What Is 11 15 As A Percent
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about 3 Of 20 Is What Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
