3 Out Of 4 Is What Percent
Kalali
Apr 13, 2025 · 5 min read
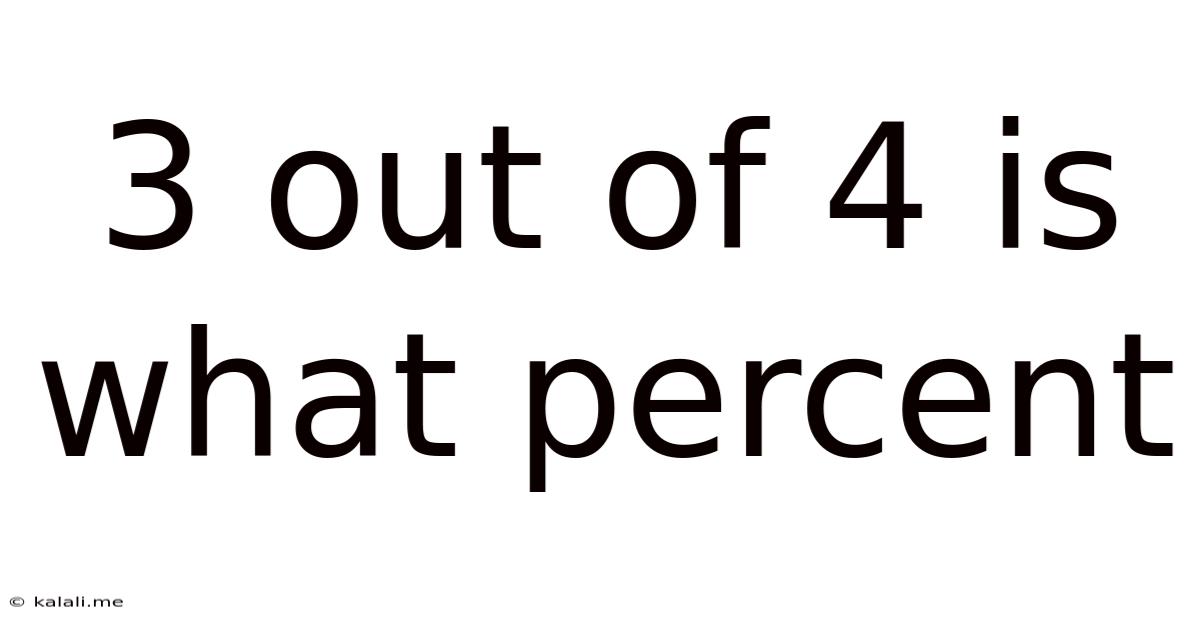
Table of Contents
3 Out of 4 is What Percent? A Comprehensive Guide to Percentage Calculations
Meta Description: Understanding percentages is crucial in many aspects of life. This comprehensive guide explains how to calculate percentages, focusing on the question: "3 out of 4 is what percent?" We'll explore different methods, provide practical examples, and delve into the underlying mathematical principles.
Percentages are a fundamental concept in mathematics and are used extensively in everyday life, from calculating discounts and sales tax to understanding statistics and financial reports. One common question that often arises involves determining the percentage representation of a fraction. This article specifically addresses the question: "3 out of 4 is what percent?" We'll explore several methods for solving this problem and expand on the broader context of percentage calculations.
Understanding Percentages: A Foundation
Before we tackle the specific problem, let's establish a solid understanding of what percentages represent. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" is used to denote a percentage. Essentially, it shows the proportion of a whole. For instance, 50% means 50 out of 100, or one-half.
Method 1: The Direct Proportion Method
This is perhaps the most straightforward approach to solving "3 out of 4 is what percent?". We can set up a proportion:
- 3/4 = x/100
Where:
- 3 represents the part.
- 4 represents the whole.
- x represents the unknown percentage.
- 100 represents the total percentage.
To solve for x, we cross-multiply:
- 4x = 300
Then, divide both sides by 4:
- x = 75
Therefore, 3 out of 4 is 75%.
Method 2: Converting Fraction to Decimal to Percentage
This method involves a two-step process:
-
Convert the fraction to a decimal: Divide the numerator (3) by the denominator (4): 3 ÷ 4 = 0.75
-
Convert the decimal to a percentage: Multiply the decimal by 100 and add the "%" symbol: 0.75 x 100 = 75%
Thus, we again arrive at the answer: 3 out of 4 is 75%.
Method 3: Using the Percentage Formula
The general formula for calculating percentages is:
- Percentage = (Part / Whole) x 100
In our case:
- Part = 3
- Whole = 4
Substituting these values into the formula:
- Percentage = (3/4) x 100 = 75%
Practical Applications of Percentage Calculations
Understanding how to calculate percentages is vital in various real-world scenarios. Here are a few examples:
-
Discounts: A store offers a 25% discount on an item. If the original price is $100, the discount amount is (25/100) x $100 = $25. The final price is $100 - $25 = $75.
-
Sales Tax: A 6% sales tax is added to a $50 purchase. The tax amount is (6/100) x $50 = $3. The total cost is $50 + $3 = $53.
-
Grade Calculations: A student scores 18 out of 20 on a test. Their percentage score is (18/20) x 100 = 90%.
-
Financial Statements: Analyzing financial reports often involves calculating percentages, such as profit margins, debt-to-equity ratios, and return on investment (ROI).
-
Surveys and Polls: Survey results are frequently presented as percentages. For example, 70% of respondents favored a particular candidate.
Beyond 3 out of 4: Solving Similar Problems
The methods described above can be easily adapted to solve similar percentage problems. For example:
-
2 out of 5 is what percent? (2/5) x 100 = 40%
-
5 out of 8 is what percent? (5/8) x 100 = 62.5%
-
12 out of 15 is what percent? (12/15) x 100 = 80%
Dealing with More Complex Scenarios
While the examples above are relatively straightforward, percentage calculations can become more complex. Consider scenarios involving:
-
Percentages of percentages: Calculating a discount on an already discounted item.
-
Compound interest: Calculating interest earned on both the principal and accumulated interest.
-
Percentage change: Determining the percentage increase or decrease between two values.
These more advanced calculations typically require a deeper understanding of mathematical principles and may involve multiple steps.
Using Technology for Percentage Calculations
Spreadsheets like Microsoft Excel and Google Sheets offer built-in functions to simplify percentage calculations. These tools can automate the process and handle more complex scenarios efficiently. Calculators, both physical and digital, also offer percentage calculation features.
Common Mistakes to Avoid
When working with percentages, several common mistakes can occur:
-
Incorrectly identifying the part and the whole: Ensure you accurately define which value represents the part and which represents the whole before applying the formula.
-
Mixing up decimals and percentages: Remember to convert decimals to percentages by multiplying by 100, and vice versa by dividing by 100.
-
Rounding errors: Be mindful of rounding errors, especially when dealing with multiple percentage calculations. It's often best to carry out calculations to several decimal places and round only at the final step.
Conclusion: Mastering Percentages for Everyday Use
The ability to confidently calculate percentages is an invaluable skill in numerous contexts. Whether it’s managing personal finances, interpreting data, or solving everyday problems, understanding how to convert fractions to percentages and apply the percentage formula is crucial. By understanding the methods outlined in this article, you'll be well-equipped to tackle a wide range of percentage calculations, starting with the fundamental question: "3 out of 4 is what percent?" Remember to practice regularly, and you'll soon find yourself proficient in this essential mathematical skill. The more you practice, the more comfortable and confident you'll become in applying these techniques to your everyday life and professional endeavors. This mastery of percentages will undoubtedly contribute to improved decision-making and a stronger understanding of the numerical world around us.
Latest Posts
Latest Posts
-
The Following Sequence Has Terms That Decrease Exponentially
Apr 15, 2025
-
Cuantos Grados Centigrados Son 41 Fahrenheit
Apr 15, 2025
-
What Is 135 Out Of 150
Apr 15, 2025
-
Do All Transition Metals Have 2 Valence Electrons
Apr 15, 2025
-
19 4 As A Mixed Number
Apr 15, 2025
Related Post
Thank you for visiting our website which covers about 3 Out Of 4 Is What Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.