19 4 As A Mixed Number
Kalali
Apr 15, 2025 · 5 min read
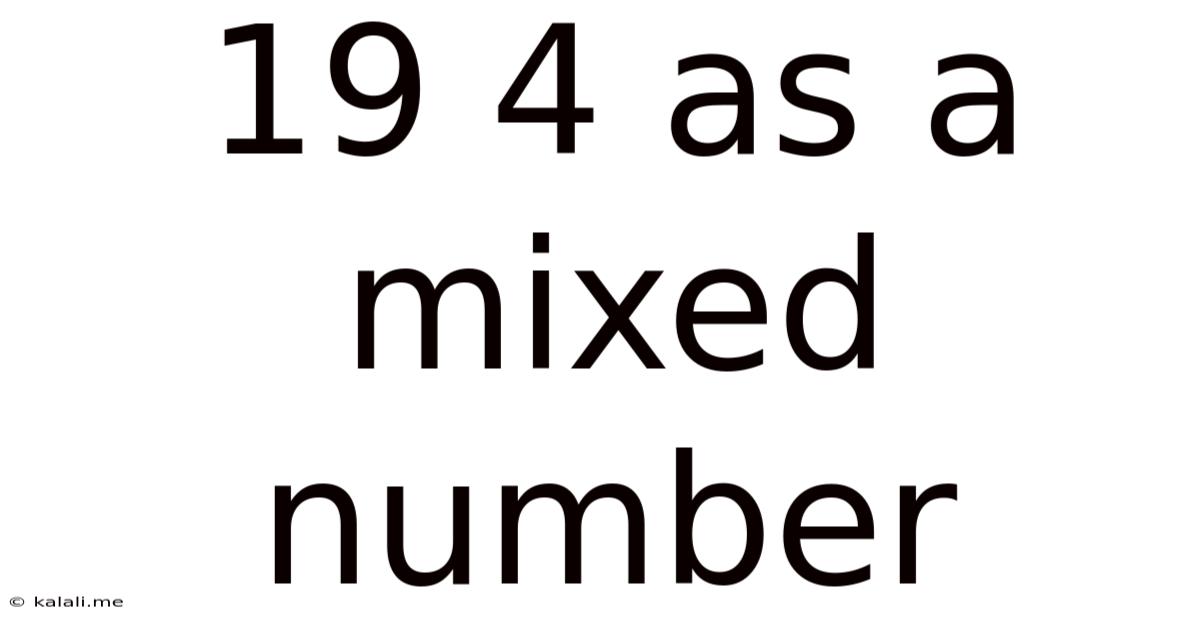
Table of Contents
19/4 as a Mixed Number: A Comprehensive Guide
Understanding fractions and how to convert them into mixed numbers is a fundamental skill in mathematics. This comprehensive guide will delve into the process of converting the improper fraction 19/4 into a mixed number, explaining the underlying concepts and providing practical examples. We'll also explore related topics, ensuring a complete understanding of this crucial mathematical operation. This article will cover various methods, cater to different learning styles, and provide ample opportunities to practice and solidify your understanding.
Meta Description: Learn how to convert the improper fraction 19/4 into a mixed number. This guide provides a step-by-step explanation, explores different methods, and includes practice problems to solidify your understanding of fraction conversion.
Understanding Improper Fractions and Mixed Numbers
Before we dive into converting 19/4, let's clarify the terms. An improper fraction is a fraction where the numerator (the top number) is greater than or equal to the denominator (the bottom number). In our case, 19/4 is an improper fraction because 19 (numerator) is larger than 4 (denominator).
A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator is smaller than the denominator. Mixed numbers provide a more intuitive way to represent quantities larger than one. For example, 2 ½ is a mixed number representing two whole units and one-half of another unit.
Method 1: Long Division
The most common and straightforward method to convert an improper fraction to a mixed number is using long division. This method helps visualize the process and reinforces fundamental arithmetic skills.
Steps:
- Divide the numerator by the denominator: Divide 19 by 4.
- Determine the whole number: The quotient (result of the division) represents the whole number part of the mixed number. 19 divided by 4 is 4 with a remainder of 3. Therefore, our whole number is 4.
- Determine the fractional part: The remainder becomes the numerator of the fractional part, and the denominator remains the same. Our remainder is 3, so the fractional part is 3/4.
- Combine the whole number and the fraction: Combine the whole number and the fractional part to form the mixed number. Therefore, 19/4 as a mixed number is 4 ¾.
Method 2: Repeated Subtraction
This method is particularly helpful for visualizing the concept of whole units within the improper fraction.
Steps:
- Subtract the denominator from the numerator repeatedly: Subtract 4 from 19 repeatedly until the result is less than the denominator (4).
- 19 - 4 = 15
- 15 - 4 = 11
- 11 - 4 = 7
- 7 - 4 = 3
- Count the number of subtractions: The number of times you subtracted the denominator represents the whole number part of the mixed number. We subtracted 4 four times, so our whole number is 4.
- The remaining value is the numerator: The remaining value after the repeated subtractions (3 in this case) becomes the numerator of the fractional part. The denominator remains the same (4).
- Combine the whole number and the fraction: This gives us the mixed number 4 ¾.
Method 3: Using Equivalent Fractions (Less Common, but Illustrative)
While less direct than long division or repeated subtraction, understanding equivalent fractions can provide a deeper insight into the conversion process.
Steps:
- Find an equivalent fraction with a numerator that is a multiple of the denominator: We need to find a multiple of 4 that is close to 19. The closest multiple is 16 (4 x 4).
- Express the improper fraction as a sum of fractions: We can rewrite 19/4 as (16/4) + (3/4).
- Simplify the whole number fraction: 16/4 simplifies to 4.
- Combine the whole number and the remaining fraction: This gives us the mixed number 4 ¾.
Visual Representation
Imagine you have 19 quarters. A quarter is represented by ¼. How many whole dollars (groups of four quarters) do you have? You have four whole dollars (4 x 4 = 16 quarters) and 3 quarters left over. This visually represents 4 ¾.
Practice Problems
To solidify your understanding, try converting the following improper fractions to mixed numbers using the methods described above:
- 23/5
- 17/6
- 31/8
- 47/12
Answers:
- 23/5 = 4 ⅗
- 17/6 = 2 ⅚
- 31/8 = 3 ⅞
- 47/12 = 3 ⅒
Why is this important?
Converting improper fractions to mixed numbers is crucial for several reasons:
- Real-world applications: Many everyday situations involve quantities that are best represented by mixed numbers. For instance, measuring ingredients in a recipe, calculating distances, or understanding time.
- Simplifying calculations: Mixed numbers often make calculations easier to understand and perform, especially when dealing with addition, subtraction, and comparison of fractions.
- Improved comprehension: Mixed numbers offer a more intuitive and easily understandable representation of quantities greater than one, compared to their improper fraction counterparts.
Further Exploration: Converting Mixed Numbers to Improper Fractions
The reverse process, converting mixed numbers back into improper fractions, is equally important. This skill is frequently needed when performing calculations involving mixed numbers. The process is as follows:
- Multiply the whole number by the denominator: For example, in the mixed number 4 ¾, multiply 4 (whole number) by 4 (denominator). This gives you 16.
- Add the numerator to the result: Add the numerator (3) to the result from step 1 (16). This gives you 19.
- Keep the same denominator: The denominator remains the same (4).
- Combine the results: This gives you the improper fraction 19/4.
Mastering the conversion between improper fractions and mixed numbers is a cornerstone of fractional arithmetic. This ability allows you to choose the most convenient representation for a given situation, simplifying calculations and improving mathematical fluency. Regular practice and application of these methods will build confidence and proficiency in handling fractions. Remember to always check your work and ensure your answer is in its simplest form.
Latest Posts
Latest Posts
-
What Percent Is 38 Of 40
Apr 16, 2025
-
How Many Quarts Is 6 Liters
Apr 16, 2025
-
How Long Is 70 Inches In Feet
Apr 16, 2025
-
What Is 2 Percent Of 25
Apr 16, 2025
-
20 Is What Percent Of 10
Apr 16, 2025
Related Post
Thank you for visiting our website which covers about 19 4 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.