30 Is 5 Percent Of What Number
Kalali
Apr 05, 2025 · 5 min read
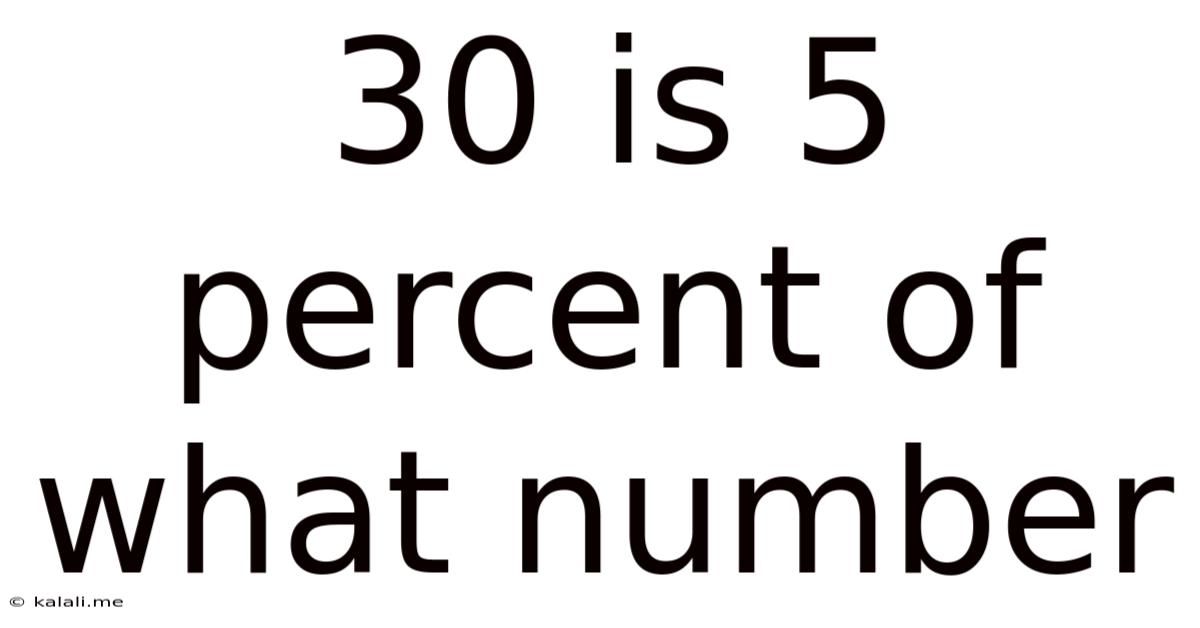
Table of Contents
30 is 5 Percent of What Number? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across various aspects of life, from calculating discounts and taxes to analyzing financial reports and understanding statistical data. This article delves deep into the question, "30 is 5 percent of what number?", providing a comprehensive guide to solving this type of problem, exploring different calculation methods, and highlighting practical applications. We'll also touch upon advanced percentage concepts and their relevance in the real world.
Understanding the Fundamentals of Percentages
Before we tackle the specific problem, let's establish a solid foundation in percentage calculations. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per cent" or "out of 100." Therefore, 5% means 5 out of 100, or 5/100, which simplifies to 1/20 as a fraction and 0.05 as a decimal.
Key Percentage Concepts:
- Part: This represents the specific portion of the whole that we are interested in. In our problem, the "part" is 30.
- Percent: This is the rate or proportion expressed as a percentage. In our problem, the "percent" is 5%.
- Whole: This represents the total amount, which is what we aim to find. This is our unknown variable (often represented by 'x').
The fundamental relationship between these elements can be expressed as:
(Part / Whole) * 100 = Percent
Solving "30 is 5 Percent of What Number?"
Now, let's apply these concepts to solve the central question: "30 is 5 percent of what number?" We can represent this problem using the equation:
30 / x * 100 = 5
To solve for 'x', we need to isolate the variable. Here's a step-by-step approach:
-
Simplify the equation: We can rewrite the equation as: (30/x) = 5/100 or (30/x) = 0.05
-
Cross-multiply: To eliminate the fraction, we cross-multiply: 30 * 100 = 5 * x
-
Solve for x: This simplifies to 3000 = 5x. To find x, we divide both sides of the equation by 5: x = 3000 / 5
-
The solution: Therefore, x = 600. This means 30 is 5 percent of 600.
Alternative Methods for Solving Percentage Problems
While the above method is straightforward, there are other approaches to solve similar percentage problems. Let's explore a few:
Method 1: Using Proportions
We can express the problem as a proportion:
30/x = 5/100
Cross-multiplying gives us: 30 * 100 = 5 * x
Solving for x yields: x = 600
Method 2: Converting Percentage to Decimal
Convert the percentage (5%) to a decimal (0.05). Then, set up the equation:
0.05 * x = 30
Solving for x: x = 30 / 0.05 = 600
Method 3: Using the Formula: Whole = Part / (Percent/100)
This formula directly calculates the whole given the part and the percentage:
Whole = 30 / (5/100) = 30 / 0.05 = 600
Practical Applications of Percentage Calculations
The ability to calculate percentages is invaluable in various real-world situations. Here are a few examples:
1. Finance and Budgeting:
- Calculating interest: Understanding interest rates and compound interest requires proficiency in percentage calculations.
- Determining discounts: Sales and discounts are often expressed as percentages. Calculating the final price after a discount involves percentage calculations.
- Analyzing financial statements: Financial reports, such as income statements and balance sheets, use percentages extensively to represent ratios and proportions.
- Tax calculations: Income tax, sales tax, and other taxes are often calculated as percentages of income or the purchase price.
2. Retail and Sales:
- Markup and markdown pricing: Businesses use percentages to determine the selling price of goods by adding a markup (percentage increase) to the cost price or reducing the price with a markdown (percentage decrease).
- Profit margin calculation: Profit margin, a crucial metric for businesses, is expressed as a percentage of sales revenue.
3. Science and Statistics:
- Data analysis: Percentages are used extensively in statistics to represent proportions, frequencies, and probabilities.
- Experimental results: Scientific experiments often involve calculating percentages to represent the success rate, error margin, and other crucial metrics.
4. Everyday Life:
- Tip calculation: Calculating tips in restaurants or for service providers involves determining a percentage of the total cost.
- Understanding surveys and polls: Results of surveys and polls are often expressed as percentages to represent the proportion of people holding specific opinions.
Advanced Percentage Concepts
While the basic percentage calculations are essential, understanding more complex concepts can enhance your analytical skills.
1. Percentage Change:
This involves calculating the increase or decrease in a value expressed as a percentage. The formula is:
(New Value - Old Value) / Old Value * 100%
A positive result indicates an increase, while a negative result signifies a decrease.
2. Percentage Point Difference:
This is the arithmetic difference between two percentages. It's crucial to distinguish this from percentage change. For example, an increase from 10% to 15% is a 5 percentage point increase, but a 50% percentage change (5/10 * 100%).
3. Compound Interest:
This concept involves earning interest on both the principal amount and accumulated interest from previous periods. Calculating compound interest requires understanding exponential growth and repeated percentage calculations.
Conclusion: Mastering Percentage Calculations
Mastering percentage calculations is a valuable skill that significantly enhances your analytical abilities and problem-solving skills in various contexts. From simple everyday calculations to complex financial analyses, understanding percentages is crucial for making informed decisions and interpreting data effectively. By understanding the fundamental principles, different calculation methods, and practical applications discussed in this article, you'll be well-equipped to tackle a wide range of percentage-related problems and confidently navigate the world of numbers. Remember that consistent practice is key to mastering these concepts and applying them efficiently in your daily life and professional endeavors.
Latest Posts
Latest Posts
-
What Is 2 3 Of 100
Apr 05, 2025
-
What State Of Matter Is Lightning
Apr 05, 2025
-
Flood Waters Moving Soil From One Location To Another
Apr 05, 2025
-
What Is 9 In Fraction Form
Apr 05, 2025
-
Is 23 A Prime Or Composite
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about 30 Is 5 Percent Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
