31 Out Of 35 As A Percentage
Kalali
Apr 04, 2025 · 4 min read
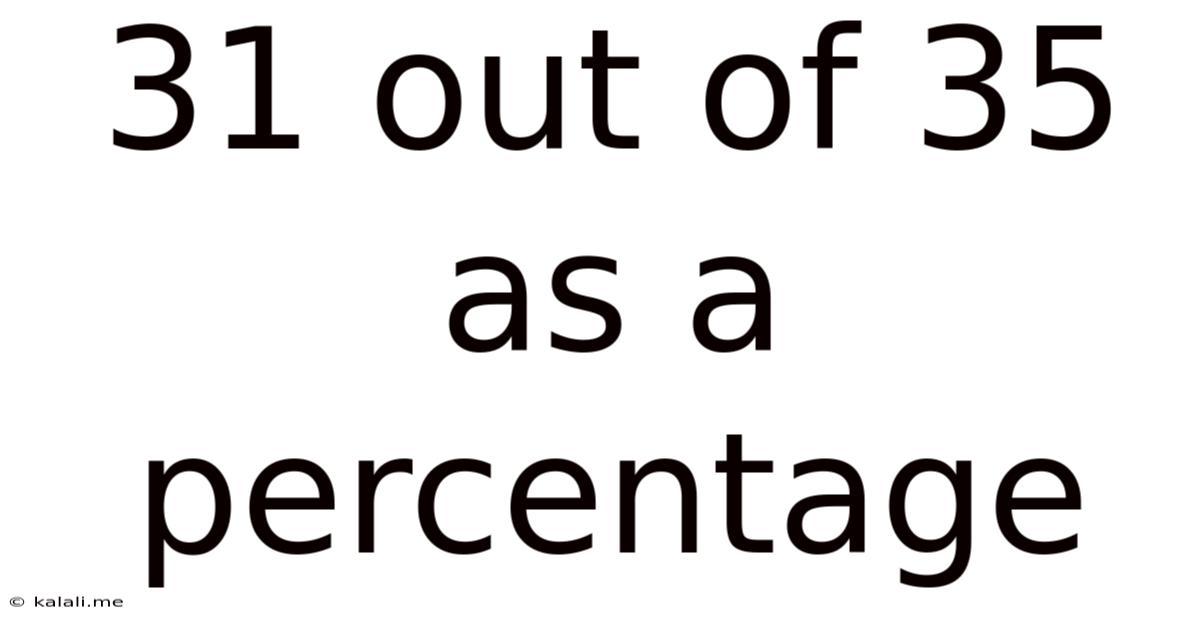
Table of Contents
31 out of 35 as a Percentage: A Comprehensive Guide
Calculating percentages is a fundamental skill with applications spanning various fields, from academic assessments to financial analysis. Understanding how to convert fractions into percentages is crucial for interpreting data, making informed decisions, and effectively communicating numerical information. This comprehensive guide delves into the calculation of "31 out of 35 as a percentage," exploring the process, practical applications, and related concepts.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "out of one hundred." For instance, 50% represents 50 out of 100, or 50/100, which simplifies to 1/2. Percentages are widely used because they provide a standardized and easily understandable way to compare proportions and ratios.
Calculating 31 out of 35 as a Percentage
The core of this problem lies in understanding the relationship between the given numbers (31 and 35) and the concept of percentage. We can represent "31 out of 35" as a fraction: 31/35. To convert this fraction into a percentage, we follow these steps:
Step 1: Convert the fraction to a decimal.
To do this, we divide the numerator (31) by the denominator (35):
31 ÷ 35 ≈ 0.8857
Step 2: Convert the decimal to a percentage.
To convert a decimal to a percentage, we multiply the decimal by 100 and add the "%" symbol:
0.8857 × 100 ≈ 88.57%
Therefore, 31 out of 35 is approximately 88.57%.
Alternative Calculation Methods
While the above method is straightforward, alternative approaches can provide valuable insights and enhance understanding.
Method 1: Using Proportions
We can set up a proportion to solve this problem. Let 'x' represent the percentage we are trying to find:
31/35 = x/100
To solve for 'x', we cross-multiply:
35x = 3100
x = 3100/35 ≈ 88.57
Therefore, x ≈ 88.57%, confirming our previous result.
Method 2: Using a Calculator
Most calculators have a percentage function. Simply enter 31 ÷ 35 and then multiply by 100 to obtain the percentage.
Practical Applications of Percentage Calculations
The ability to calculate percentages accurately has numerous practical applications in daily life and professional settings. Here are a few examples:
1. Academic Performance
Students frequently encounter percentage calculations when determining their grades. For instance, if a student answers 31 questions correctly out of a total of 35, their score is 88.57%. This percentage helps assess their understanding of the subject matter.
2. Financial Calculations
Percentages are fundamental in financial calculations. Calculating interest rates, discounts, tax rates, profit margins, and investment returns all involve percentage calculations. For example, understanding the percentage increase or decrease in your savings account balance over time is crucial for financial planning.
3. Sales and Marketing
Businesses use percentages extensively in sales and marketing. Discounts are often expressed as percentages (e.g., "20% off"), and sales figures are frequently analyzed as percentages of total revenue. Understanding market share percentages helps businesses assess their competitive position.
4. Data Analysis and Statistics
Percentages are used to represent data in various statistical contexts. Survey results, demographic information, and scientific findings often utilize percentages to present data clearly and concisely. For instance, calculating the percentage of respondents who favor a particular political candidate is essential for understanding public opinion.
5. Everyday Life
Beyond formal contexts, percentage calculations are frequently used in everyday life. Determining the tip amount in a restaurant, calculating the discount on sale items, or understanding the nutritional content of food products often involves working with percentages.
Rounding Percentages
The result of 31 out of 35 as a percentage is 88.57%. Depending on the context, it might be necessary to round this figure. Rounding to the nearest whole number gives 89%. Rounding to one decimal place maintains 88.6%. The choice of rounding depends on the required level of precision. In many cases, rounding to one decimal place (88.6%) offers a good balance between precision and simplicity.
Common Mistakes to Avoid
Several common mistakes can lead to inaccurate percentage calculations:
- Incorrect order of operations: Ensure you perform the division before multiplying by 100.
- Misinterpreting the fraction: Make sure you correctly identify the numerator (the part) and the denominator (the whole).
- Rounding errors: Be mindful of rounding errors, especially when working with multiple steps. It's generally advisable to keep extra decimal places during intermediate calculations and round only the final result.
Expanding Your Understanding: Further Exploration
Mastering percentage calculations opens doors to more advanced mathematical concepts. Consider exploring:
- Compound interest: Understanding how interest accrues over time, incorporating the effect of compounding.
- Percentage change: Calculating the percentage increase or decrease between two values.
- Statistical analysis: Using percentages to interpret data and draw meaningful conclusions.
- Financial modeling: Applying percentage calculations in financial models for forecasting and decision-making.
Conclusion
Calculating 31 out of 35 as a percentage – approximately 88.57% – involves a simple yet powerful mathematical process with far-reaching implications. This seemingly basic calculation forms the bedrock of numerous real-world applications, underscoring the importance of mastering percentage calculations. By understanding the different methods and avoiding common pitfalls, you can confidently tackle percentage problems and utilize this fundamental skill to analyze data, make informed decisions, and communicate numerical information effectively. The ability to confidently and accurately convert fractions to percentages is a valuable skill that transcends academic settings and extends into diverse areas of life and professional endeavors.
Latest Posts
Latest Posts
-
An Ice Cube Contains A Large Air Bubble
Apr 11, 2025
-
How Many Centimeters Is 8 Ft
Apr 11, 2025
-
60 Degrees Fahrenheit Equals What In Celsius
Apr 11, 2025
-
Least Common Multiple Of 20 And 15
Apr 11, 2025
-
What Percent Of 80 Is 40
Apr 11, 2025
Related Post
Thank you for visiting our website which covers about 31 Out Of 35 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.