What Percent Of 80 Is 40
Kalali
Apr 11, 2025 · 5 min read
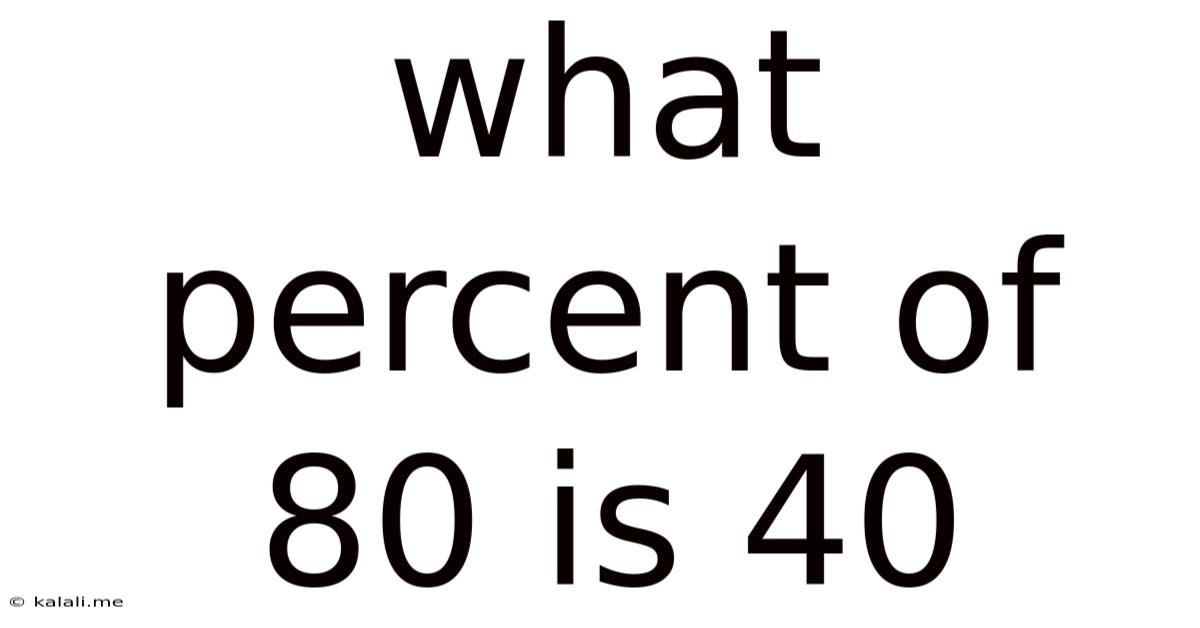
Table of Contents
What Percent of 80 is 40? A Deep Dive into Percentages and Their Applications
This seemingly simple question, "What percent of 80 is 40?", opens the door to a fascinating exploration of percentages, their practical applications, and the underlying mathematical principles. While the answer itself is straightforward, understanding the how and why behind the calculation provides a robust foundation for tackling more complex percentage problems. This article will not only provide the solution but delve into the various methods for solving percentage problems, explore real-world examples, and discuss the importance of percentage calculations in diverse fields.
Meta Description: Discover how to calculate what percent of 80 is 40. This comprehensive guide explores various methods, real-world applications, and the underlying mathematical principles of percentage calculations. Learn to master percentages with ease!
Understanding Percentages: The Basics
Before jumping into the solution, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a number out of 100. The symbol "%" signifies "per hundred" or "out of 100." For instance, 50% represents 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Percentages are ubiquitous in everyday life, used to represent various proportions and ratios. We encounter them in discounts (e.g., 20% off), interest rates (e.g., 5% annual interest), statistical data (e.g., 75% of respondents agreed), and much more. Understanding percentages is therefore crucial for navigating various aspects of life, from personal finance to scientific analysis.
Method 1: Using the Percentage Formula
The most common method for solving percentage problems involves using the basic percentage formula:
(Part / Whole) x 100% = Percentage
In our problem, "What percent of 80 is 40?", we can identify:
- Part: 40 (the portion we're interested in)
- Whole: 80 (the total amount)
Substituting these values into the formula:
(40 / 80) x 100% = 0.5 x 100% = 50%
Therefore, 40 is 50% of 80.
Method 2: Setting up a Proportion
Another effective method involves setting up a proportion. A proportion is an equation stating that two ratios are equal. We can represent our problem as:
40 / 80 = x / 100
Where 'x' represents the unknown percentage. To solve for 'x', we can cross-multiply:
40 * 100 = 80 * x
4000 = 80x
x = 4000 / 80
x = 50
Thus, x = 50%, confirming our previous result. This method is particularly useful for visualizing the relationship between the parts and the whole.
Method 3: Using Decimal Equivalents
Percentages can also be easily converted to decimals. To do this, we divide the percentage by 100. For example, 50% is equivalent to 0.5 (50/100).
We can use this approach to solve our problem as follows:
-
Convert the percentage to a decimal: Let's assume 'x' represents the percentage we are trying to find. We can write this as x/100.
-
Set up the equation: (x/100) * 80 = 40
-
Solve for 'x': Multiply both sides by 100: x * 80 = 4000
-
Divide both sides by 80: x = 4000 / 80 = 50
Therefore, the percentage is 50%.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is invaluable in a wide range of situations. Here are a few examples:
-
Finance: Calculating interest earned on savings accounts, determining loan payments, understanding discounts and sales tax, analyzing investment returns, and budgeting personal expenses all rely heavily on percentage calculations. Understanding percentage change is crucial for tracking financial growth or decline.
-
Retail: Retailers use percentages to calculate discounts, markups, and profit margins. Understanding these calculations is crucial for both consumers and businesses. Sales promotions, clearance pricing, and even loyalty programs all involve percentage-based calculations.
-
Science and Statistics: Percentages are fundamental in scientific research and data analysis. Researchers often express results as percentages to represent proportions and trends within data sets. This applies to fields like epidemiology, demographics, and various scientific experiments.
-
Education: Students’ grades are often expressed as percentages, representing the proportion of correct answers or the overall performance in a course. Calculating grade point averages (GPAs) also involves percentage calculations.
-
Everyday Life: Calculating tips at restaurants, understanding sales tax on purchases, and determining the percentage of ingredients in a recipe all involve basic percentage calculations.
Beyond the Basics: Percentage Increase and Decrease
Understanding percentage increase and decrease is crucial for more advanced applications. These calculations involve finding the percentage change between two values.
Percentage Increase: The formula is:
[(New Value - Old Value) / Old Value] x 100%
Percentage Decrease: The formula is:
[(Old Value - New Value) / Old Value] x 100%
For example, if a product's price increases from $50 to $60, the percentage increase is:
[(60 - 50) / 50] x 100% = 20%
Similarly, if the price decreases from $60 to $50, the percentage decrease is:
[(60 - 50) / 60] x 100% ≈ 16.67%
Troubleshooting Common Percentage Problems
While percentage calculations are relatively straightforward, some common mistakes can arise:
-
Incorrect Formula Application: Ensuring the correct formula is used for the specific problem is crucial. Confusing the 'part' and 'whole' in the formula can lead to incorrect results.
-
Decimal Errors: Errors in decimal manipulation, especially during multiplication and division, can impact accuracy. Using a calculator carefully and double-checking calculations can minimize such errors.
-
Percentage Change Misinterpretations: Incorrectly interpreting percentage increase or decrease, especially when dealing with multiple percentage changes, can lead to misleading conclusions.
-
Failing to Convert Percentages to Decimals: Forgetting to convert percentages to decimals (by dividing by 100) before using them in calculations will result in incorrect answers.
Conclusion: Mastering Percentages for a More Numerate Life
The seemingly simple question, "What percent of 80 is 40?", has led us on a journey through the world of percentages. We've explored various methods for solving percentage problems, delved into real-world applications, and highlighted common pitfalls to avoid. Mastering percentage calculations is not merely about solving mathematical problems; it's about developing a crucial life skill applicable across numerous domains. From managing personal finances to understanding complex data, the ability to confidently work with percentages empowers individuals to make informed decisions and navigate the quantitative aspects of everyday life with greater ease and accuracy. The foundation laid here allows you to confidently tackle more complex percentage problems and apply this vital mathematical skill in various aspects of your personal and professional life.
Latest Posts
Latest Posts
-
How Many Hours Is 200 Mins
Apr 18, 2025
-
59 Centimeters Is How Many Inches
Apr 18, 2025
-
How Many Liters Is 64 Oz Of Water
Apr 18, 2025
-
What Is 30 Out Of 40
Apr 18, 2025
-
What Percent Is 3 Of 7
Apr 18, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 80 Is 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.