31 Out Of 36 As A Percentage
Kalali
Aug 26, 2025 · 5 min read
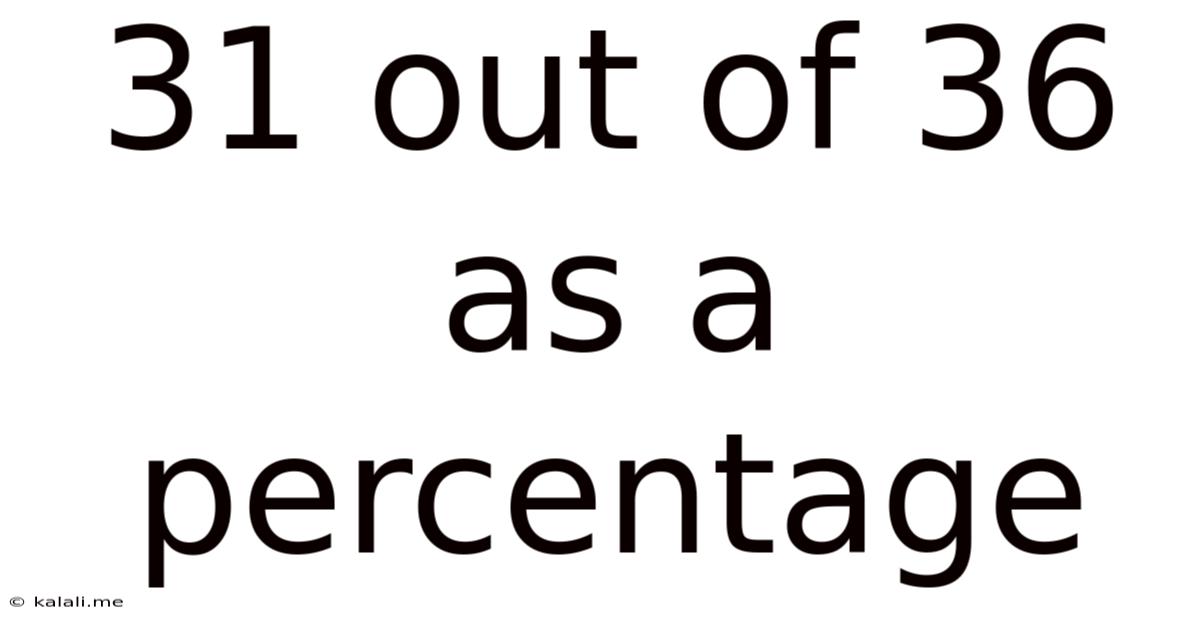
Table of Contents
31 out of 36 as a Percentage: A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill in many areas of life, from academic pursuits and financial management to everyday tasks. Understanding how to convert fractions to percentages is crucial for interpreting data, making informed decisions, and effectively communicating numerical information. This article delves into the specific calculation of 31 out of 36 as a percentage, providing a step-by-step explanation, exploring related concepts, and offering practical applications. This comprehensive guide will equip you with the knowledge to confidently handle similar percentage calculations in the future.
What is a Percentage?
Before we dive into the specific calculation, let's clarify the concept of a percentage. A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred" (per centum in Latin). Percentages are widely used because they provide a standardized and easily understandable way to compare proportions and ratios.
Calculating 31 out of 36 as a Percentage: A Step-by-Step Approach
To calculate 31 out of 36 as a percentage, we follow these simple steps:
-
Express the values as a fraction: The phrase "31 out of 36" can be written as the fraction 31/36.
-
Convert the fraction to a decimal: Divide the numerator (31) by the denominator (36). This gives us: 31 ÷ 36 ≈ 0.8611
-
Convert the decimal to a percentage: Multiply the decimal by 100. This moves the decimal point two places to the right. 0.8611 x 100 = 86.11%
Therefore, 31 out of 36 is approximately 86.11%.
Understanding the Calculation: A Deeper Dive
The process of converting a fraction to a percentage involves essentially scaling the fraction to have a denominator of 100. This allows for easy comparison with other percentages. Let's break down the logic behind each step:
-
Fraction to Decimal: Dividing the numerator by the denominator transforms the fraction into a decimal representation, indicating the proportion of the whole.
-
Decimal to Percentage: Multiplying by 100 simply scales this proportion to represent it as a fraction of 100, thereby giving us the percentage.
Rounding and Precision in Percentage Calculations
In many cases, percentage calculations result in decimal values. The level of precision required depends on the context. For instance, in financial calculations, high precision is often necessary, while in informal settings, rounding to the nearest whole number might suffice. In our example, 86.11% is a reasonably precise representation. However, depending on the application, you might round it to 86% or even 86.1%. Always consider the context and the level of accuracy required when rounding percentages.
Practical Applications of Percentage Calculations
Percentage calculations are ubiquitous in various aspects of daily life and professional fields. Here are a few examples:
-
Academic Performance: Calculating grades, exam scores, and overall academic performance often involves percentage calculations. For example, if a student scores 28 out of 35 on a test, the percentage score is calculated as (28/35) * 100 = 80%.
-
Financial Management: Percentages are fundamental in finance, used for calculating interest rates, discounts, taxes, profit margins, and investment returns.
-
Sales and Marketing: Sales figures, market share, conversion rates, and customer satisfaction rates are frequently expressed as percentages.
-
Data Analysis: Percentages are crucial for interpreting data, making comparisons, and drawing conclusions from statistical information. For example, analyzing survey results often involves expressing responses as percentages of the total number of respondents.
-
Sports Statistics: Batting averages in baseball, free-throw percentages in basketball, and winning percentages in various sports all rely on percentage calculations.
Related Percentage Calculations and Concepts
Understanding the calculation of 31 out of 36 as a percentage provides a foundation for tackling other percentage-related problems. Here are some related concepts:
-
Calculating the Percentage Increase or Decrease: This involves determining the percentage change between two values. The formula is: [(New Value - Old Value) / Old Value] * 100.
-
Finding a Percentage of a Number: This involves multiplying a number by a percentage (expressed as a decimal). For example, finding 20% of 50 is 50 * 0.20 = 10.
-
Working Backwards from a Percentage: This involves finding the original value when given a percentage and the resulting value. For instance, if 15% of a number is 30, the original number is 30 / 0.15 = 200.
Using Technology for Percentage Calculations
While manual calculations are useful for understanding the underlying concepts, technology can significantly streamline the process, especially for more complex calculations. Many calculators, spreadsheet software (like Microsoft Excel or Google Sheets), and online calculators are readily available for performing percentage calculations efficiently.
Avoiding Common Mistakes in Percentage Calculations
Several common mistakes can occur when working with percentages. Being mindful of these pitfalls can help ensure accuracy:
-
Incorrect Order of Operations: Always follow the order of operations (PEMDAS/BODMAS) to avoid errors in calculations involving multiple operations.
-
Misinterpreting Percentages: Clearly understand what the percentage represents and what the base value is.
-
Rounding Errors: Be mindful of the level of precision required and round appropriately to avoid significant inaccuracies.
-
Using the Wrong Formula: Use the correct formula depending on the specific type of percentage calculation being performed.
Conclusion: Mastering Percentage Calculations
The ability to calculate percentages is an invaluable skill with broad applicability. Understanding the fundamental principles and common pitfalls, as outlined in this article, empowers individuals to confidently handle percentage calculations in diverse settings. From everyday tasks to complex financial analysis, the ability to accurately and efficiently determine percentages contributes to informed decision-making and a deeper understanding of numerical data. Remember the core steps: convert to a fraction, then to a decimal, and finally multiply by 100 to obtain the percentage. Practice makes perfect, so keep practicing your percentage skills to master this essential mathematical tool. The calculation of 31 out of 36 as a percentage, specifically 86.11%, serves as a practical example that can be extended to countless other applications.
Latest Posts
Latest Posts
-
What Do You Call A One Eyed Deer
Aug 26, 2025
-
What Question Did Charles Darwin Attempt To Answer
Aug 26, 2025
-
Least Common Multiple Of 18 And 30
Aug 26, 2025
-
What Is 1 1 2 Cups Divided By 4
Aug 26, 2025
-
Is Adam Levine Related To Avril Lavigne
Aug 26, 2025
Related Post
Thank you for visiting our website which covers about 31 Out Of 36 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.