32 Is What Percent Of 80
Kalali
Apr 18, 2025 · 6 min read
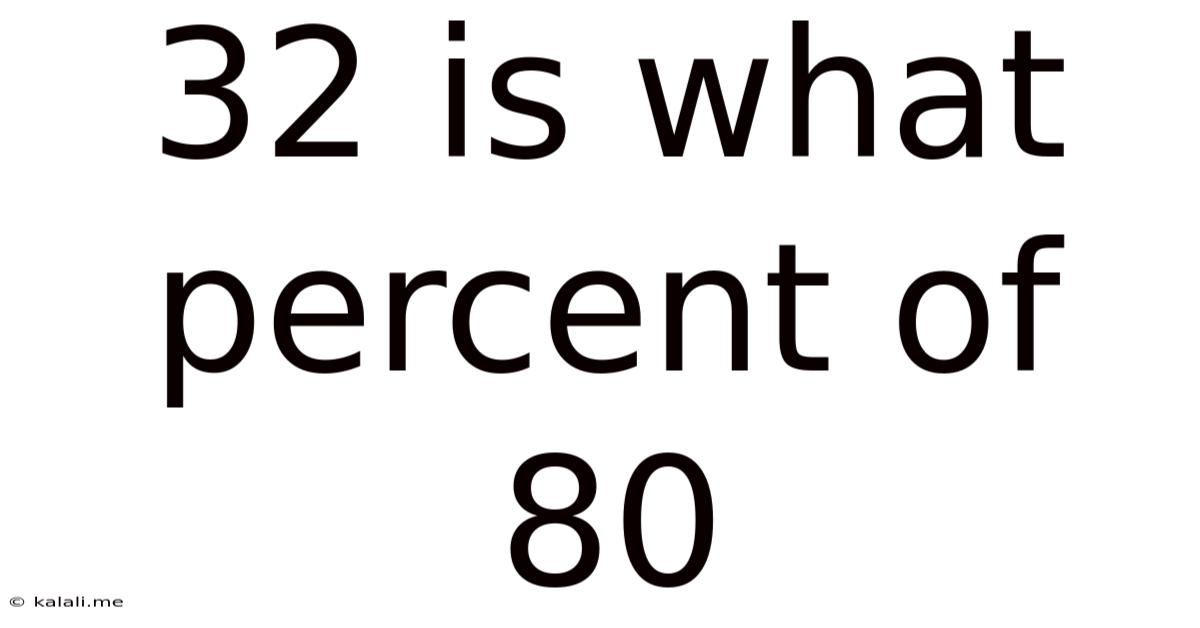
Table of Contents
32 is What Percent of 80: A Deep Dive into Percentage Calculations and Real-World Applications
Understanding percentages is a fundamental skill applicable across numerous aspects of life, from calculating discounts and taxes to analyzing data and understanding financial reports. This article will thoroughly explore how to determine what percentage 32 represents of 80, going beyond a simple answer to delve into the underlying principles, different calculation methods, and real-world examples to solidify your understanding. We'll cover various approaches, including the standard formula, cross-multiplication, and even a simplified mental math trick for similar problems. This comprehensive guide aims to equip you with not just the answer but a complete grasp of percentage calculations.
Meta Description: Learn how to calculate what percentage 32 is of 80. This article provides multiple methods, real-world examples, and practical applications of percentage calculations, making it a comprehensive guide for understanding this essential mathematical concept.
Understanding the Basics of Percentages
Before diving into the specifics of calculating "32 is what percent of 80?", let's establish a solid foundation in percentage concepts. A percentage is simply a fraction expressed as a part of 100. The term "percent" itself comes from the Latin "per centum," meaning "out of one hundred." Therefore, 50% means 50 out of 100, which is equivalent to 1/2 or 0.5 in decimal form.
Understanding this fundamental concept is crucial for accurately interpreting and applying percentages in various contexts. Whether you're calculating sales tax, figuring out discounts, or analyzing statistical data, the ability to translate percentages into fractions or decimals is key.
Method 1: The Standard Percentage Formula
The most straightforward approach to solving "32 is what percent of 80?" involves using the standard percentage formula:
(Part / Whole) * 100 = Percentage
In this case:
- Part: 32 (the value we want to express as a percentage)
- Whole: 80 (the total value)
Applying the formula:
(32 / 80) * 100 = 40%
Therefore, 32 is 40% of 80.
Method 2: Cross-Multiplication
Cross-multiplication offers an alternative method for solving percentage problems, particularly useful when dealing with more complex scenarios. We can set up a proportion:
32 / 80 = x / 100
Where 'x' represents the unknown percentage. Cross-multiplying gives us:
32 * 100 = 80 * x
3200 = 80x
Solving for x:
x = 3200 / 80 = 40
Therefore, x = 40%, confirming our previous result. This method is especially helpful when the numbers involved are less straightforward or require more manipulation.
Method 3: Simplifying Fractions (Mental Math Trick)
For simpler percentage problems like this one, a mental math approach using fraction simplification can be quite efficient. Notice that 32 is a simple fraction of 80:
32/80 can be simplified by dividing both the numerator and the denominator by their greatest common divisor, which is 16:
32 ÷ 16 = 2 80 ÷ 16 = 5
This simplifies the fraction to 2/5. To convert this fraction to a percentage, we can find an equivalent fraction with a denominator of 100:
2/5 = (2 * 20) / (5 * 20) = 40/100
Therefore, 2/5 is equal to 40%, providing a quick and efficient way to solve the problem mentally. This method is particularly useful for improving your mental math skills and quickly solving percentage problems in everyday scenarios.
Real-World Applications: Understanding the Significance of 40%
The answer – 40% – isn't just a number; it has significant real-world implications. Let's explore a few examples:
-
Sales and Discounts: Imagine a store offering a discount. If an item originally costs $80 and is discounted by $32, the discount is 40%. This is crucial information for consumers to compare prices and make informed purchasing decisions. Understanding percentage discounts helps consumers calculate the final price effectively and quickly.
-
Financial Analysis: In finance, percentages are used extensively to analyze financial performance. If a company's profits were $32 million against a revenue of $80 million, its profit margin is 40%. This percentage provides vital insights into the company's efficiency and profitability, informing investment decisions and strategic planning.
-
Test Scores and Grades: If a student answers 32 out of 80 questions correctly on a test, their score is 40%. This immediately translates to a grade, providing clear feedback on their performance and areas for improvement. Understanding percentages in this context helps students and educators track academic progress and identify learning needs.
-
Surveys and Polls: In surveys, percentages are used to represent the proportion of respondents holding particular views. For instance, if 32 out of 80 respondents favor a particular policy, the support is 40%. This provides a clear and easily understood representation of public opinion. This is crucial for researchers, policymakers, and the media to interpret and report the data effectively.
-
Data Analysis and Statistics: Percentages are fundamental in statistical analysis. They represent proportions within larger datasets, making it easier to compare and interpret data across different categories or groups. In market research, for instance, 40% could represent the market share held by a particular product or brand.
These examples highlight how understanding percentage calculations and their applications is essential for informed decision-making in various fields. The ability to quickly and accurately interpret percentages significantly enhances your analytical capabilities and problem-solving skills.
Expanding Your Knowledge: More Complex Percentage Problems
While the problem "32 is what percent of 80?" is relatively straightforward, the principles discussed can be applied to more complex scenarios. For example:
-
Finding the Whole: You might be given a percentage and the part and need to find the whole. For instance: "40% of what number is 32?" This requires a slightly different approach to the formula.
-
Finding the Part: Conversely, you could be given the percentage and the whole and need to find the part. For example: "What is 40% of 80?" This involves multiplying the whole by the decimal equivalent of the percentage.
-
Percentage Increase and Decrease: Calculations involving percentage increases or decreases often involve adding or subtracting the percentage change from the original value. Understanding these calculations is crucial for analyzing growth rates, inflation, or discounts.
-
Compound Percentage Changes: These calculations involve applying percentage changes sequentially, resulting in a compounding effect. For instance, calculating the final price after successive discounts or interest accrual over time requires a more nuanced understanding of percentage calculations.
Conclusion: Mastering the Art of Percentage Calculations
Understanding how to calculate "32 is what percent of 80?" is more than just solving a simple math problem. It's about grasping a fundamental concept that has wide-ranging applications in everyday life and various professional contexts. By mastering the different methods outlined in this article, from the standard formula to mental math tricks, you'll equip yourself with a valuable skill that will enhance your analytical abilities and help you make informed decisions in numerous situations. Remember, the key is to understand the underlying principles and practice applying them to different real-world scenarios. The more you practice, the more comfortable and proficient you'll become in tackling percentage problems of any complexity. So, start practicing and see how easily you can incorporate these techniques into your daily routine!
Latest Posts
Latest Posts
-
What Is 8 10 As A Percentage
Apr 22, 2025
-
How Many Miles Is 100 000 Kilometers
Apr 22, 2025
-
How Many Inches In 98 Cm
Apr 22, 2025
-
What Lifestyle Choices Can Help Reduce The Risk Of Suicide
Apr 22, 2025
-
What Are Holes In A Graph
Apr 22, 2025
Related Post
Thank you for visiting our website which covers about 32 Is What Percent Of 80 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.