33 Out Of 35 As A Percentage
Kalali
Apr 24, 2025 · 5 min read
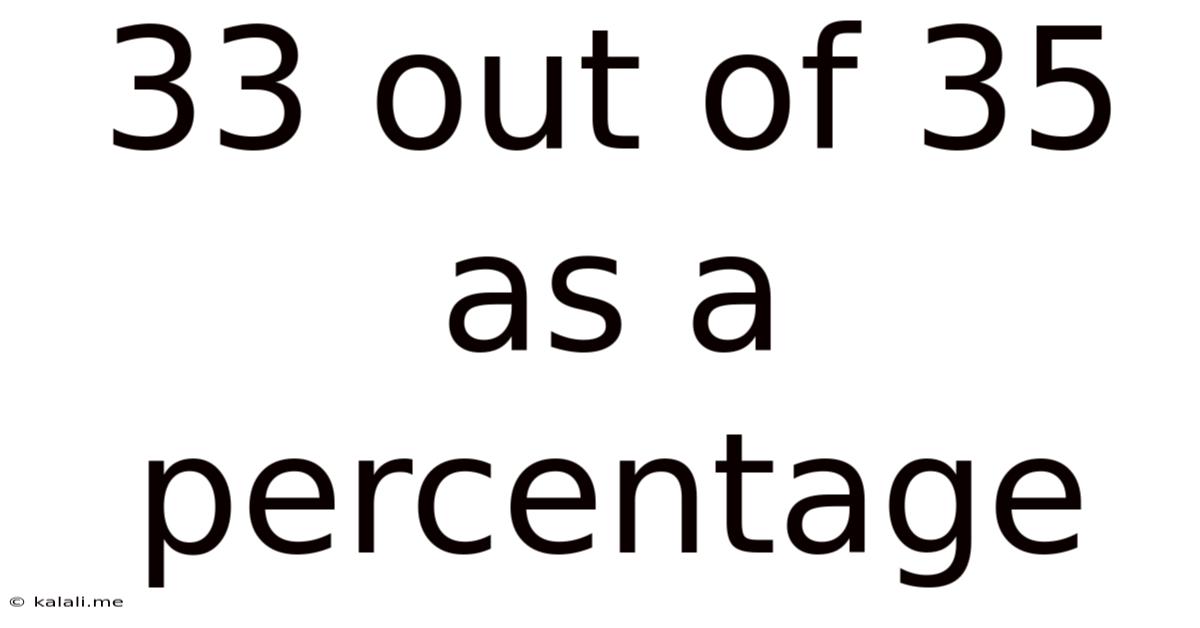
Table of Contents
Decoding 33 out of 35: A Comprehensive Guide to Percentage Calculations and Applications
Calculating percentages is a fundamental skill applicable across various fields, from academic assessments to financial analysis. Understanding how to convert fractions and ratios into percentages is crucial for interpreting data and making informed decisions. This article dives deep into calculating 33 out of 35 as a percentage, exploring the methodology, practical applications, and broader implications of percentage calculations. We'll also examine different methods and offer tips for accuracy and efficiency.
What is a Percentage?
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "per hundred." Therefore, 50% means 50 out of 100, or 50/100, which simplifies to 1/2. Percentages are used extensively to represent proportions, rates, and changes in various contexts.
Calculating 33 out of 35 as a Percentage: The Basic Method
The most straightforward way to calculate 33 out of 35 as a percentage involves three simple steps:
-
Form a Fraction: Express the given numbers as a fraction: 33/35. This represents the portion (33) out of the total (35).
-
Convert to Decimal: Divide the numerator (33) by the denominator (35): 33 ÷ 35 ≈ 0.942857
-
Multiply by 100: Multiply the decimal result by 100 to express it as a percentage: 0.942857 × 100 ≈ 94.29%
Therefore, 33 out of 35 is approximately 94.29%. Rounding is often necessary to express percentages with manageable precision. In this case, rounding to two decimal places provides a sufficient level of accuracy.
Alternative Calculation Methods
While the basic method is efficient, other approaches can be used, especially when dealing with more complex calculations or when working without a calculator:
-
Using Proportions: You can set up a proportion to solve for the percentage. Let 'x' be the percentage:
33/35 = x/100
Cross-multiplying gives: 3300 = 35x
Solving for x: x = 3300/35 ≈ 94.29%
-
Using a Calculator with Percentage Function: Many calculators have a dedicated percentage function (%) that simplifies the calculation. Simply enter 33 ÷ 35 × 100 and press the % button (or a similar function). The calculator will directly output the percentage.
-
Mental Estimation: For quick estimations, you can round the numbers to make the calculation easier. For example, 33 is close to 35, so you could estimate the percentage to be around 95%. This method is useful for quickly assessing the magnitude of the percentage, though it sacrifices precision.
Practical Applications of Percentage Calculations
The ability to calculate percentages is invaluable in numerous real-world scenarios:
-
Academic Performance: Calculating grades, scores on tests, and overall academic performance frequently involves percentages. A student scoring 33 out of 35 on a quiz would achieve a grade of approximately 94.29%.
-
Financial Management: Percentages are crucial in finance, including calculating interest rates, discounts, taxes, profit margins, and investment returns. Understanding percentage changes in stock prices, for example, is essential for informed investment decisions.
-
Data Analysis and Statistics: Percentages are fundamental in statistical analysis, allowing researchers to express data as proportions, calculate probabilities, and compare different datasets.
-
Business and Marketing: Businesses use percentages to track sales figures, market share, customer satisfaction, and conversion rates. Marketing campaigns often analyze success rates and ROI (Return on Investment) using percentage calculations.
-
Everyday Life: Calculating tips in restaurants, understanding sales discounts in stores, or figuring out the percentage of ingredients in a recipe all involve percentage calculations.
Error Handling and Precision
When working with percentages, it's crucial to be mindful of potential sources of error:
-
Rounding Errors: Rounding intermediate calculations can lead to slight inaccuracies in the final result. It's often best to avoid rounding until the final step to maintain precision.
-
Significant Figures: The number of significant figures in your answer should reflect the precision of the input data. If the original numbers have limited precision, then the resulting percentage should also be rounded accordingly.
-
Data Interpretation: Always carefully consider the context of the percentage. A high percentage doesn't always imply a positive outcome, and a low percentage doesn't necessarily indicate failure. The interpretation should be informed by the specific situation.
Beyond 33 out of 35: Expanding Your Percentage Skills
Understanding how to calculate 33 out of 35 as a percentage provides a foundation for tackling a wide range of percentage-related problems. Here are some further points to consider:
-
Calculating Percentage Increase/Decrease: This involves determining the percentage change between two values. The formula is: [(New Value - Old Value) / Old Value] × 100.
-
Finding the Original Value: If you know the percentage and the resulting value, you can calculate the original value using algebraic manipulation.
-
Working with Complex Percentages: Some calculations might involve multiple percentages, such as compound interest or successive discounts. These require a systematic approach to ensure accuracy.
-
Using Spreadsheet Software: Software like Microsoft Excel or Google Sheets provides built-in functions for percentage calculations, simplifying complex tasks.
Conclusion:
Calculating 33 out of 35 as a percentage, which equates to approximately 94.29%, is a straightforward yet essential skill. The ability to accurately and efficiently calculate percentages is a valuable asset in many areas of life, from academic pursuits to professional endeavors. By mastering the fundamental methods and understanding the practical applications, you can confidently navigate situations involving percentages and utilize this knowledge to make informed decisions. Remember to practice regularly and utilize available tools to enhance your proficiency in this fundamental mathematical skill. The more you practice, the more intuitive and effortless percentage calculations will become.
Latest Posts
Latest Posts
-
What Is 140 Minutes In Hours
Apr 24, 2025
-
200 Grams Is Equal To How Many Ounces
Apr 24, 2025
-
12 Out Of 20 As A Grade
Apr 24, 2025
-
What Are The Defined Terms In Geometry
Apr 24, 2025
-
What Percent Of 45 Is 9
Apr 24, 2025
Related Post
Thank you for visiting our website which covers about 33 Out Of 35 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.