4 1/2 As An Improper Fraction
Kalali
Apr 03, 2025 · 5 min read
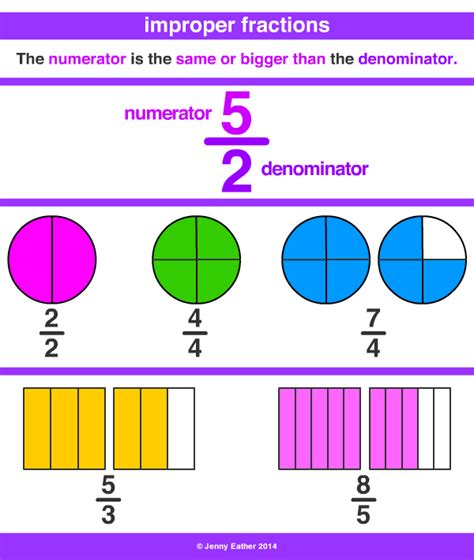
Table of Contents
4 1/2 as an Improper Fraction: A Comprehensive Guide
Understanding fractions is fundamental to mathematics, and converting mixed numbers into improper fractions is a crucial skill. This comprehensive guide will delve into the process of converting the mixed number 4 1/2 into its improper fraction equivalent, explaining the underlying concepts and providing practical examples to solidify your understanding. We'll also explore the broader context of fractions, their importance, and various applications.
What is a Mixed Number?
A mixed number combines a whole number and a proper fraction. A proper fraction is one where the numerator (top number) is smaller than the denominator (bottom number). For instance, 4 1/2 is a mixed number: 4 represents the whole number, and 1/2 is the proper fraction.
What is an Improper Fraction?
An improper fraction is a fraction where the numerator is greater than or equal to the denominator. This indicates a value greater than or equal to one. Converting mixed numbers to improper fractions is often necessary for simplifying calculations and solving equations.
Converting 4 1/2 to an Improper Fraction: Step-by-Step
The conversion of 4 1/2 to an improper fraction involves a simple two-step process:
Step 1: Multiply the whole number by the denominator.
In our case, the whole number is 4, and the denominator of the fraction is 2. Multiplying these together gives us 4 * 2 = 8.
Step 2: Add the numerator to the result from Step 1.
The numerator of our fraction is 1. Adding this to the result from Step 1 (8) gives us 8 + 1 = 9.
Step 3: Keep the same denominator.
The denominator remains unchanged throughout the conversion process. Therefore, the denominator of our improper fraction will be 2.
The final result: Combining the results from Steps 2 and 3, we get the improper fraction 9/2. This means that 4 1/2 is equivalent to 9/2.
Visualizing the Conversion
Imagine you have four and a half pizzas. Each pizza is divided into two equal halves. You have four whole pizzas (4 x 2 = 8 halves) plus an additional half (1/2), totaling nine halves (9/2). This visual representation helps solidify the understanding of the conversion process.
Why is this Conversion Important?
Converting mixed numbers to improper fractions is essential for several reasons:
- Simplification of Calculations: Performing operations like addition, subtraction, multiplication, and division is often easier with improper fractions.
- Solving Equations: Many algebraic equations involving fractions require improper fractions for accurate solutions.
- Standardization: Using improper fractions ensures consistency in mathematical operations and simplifies comparisons between different fractional values.
- Real-World Applications: Many real-world applications, such as cooking, construction, and engineering, require precise fractional measurements, making the conversion between mixed numbers and improper fractions crucial.
More Examples of Converting Mixed Numbers to Improper Fractions
Let's solidify our understanding with a few more examples:
- 2 3/4: (2 * 4) + 3 = 11. The denominator remains 4. Therefore, 2 3/4 = 11/4.
- 5 1/3: (5 * 3) + 1 = 16. The denominator remains 3. Therefore, 5 1/3 = 16/3.
- 1 7/8: (1 * 8) + 7 = 15. The denominator remains 8. Therefore, 1 7/8 = 15/8.
- 3 2/5: (3 * 5) + 2 = 17. The denominator remains 5. Therefore, 3 2/5 = 17/5.
Converting Improper Fractions back to Mixed Numbers
It's equally important to understand the reverse process – converting an improper fraction back to a mixed number. This is done through division:
- Divide the numerator by the denominator. The quotient becomes the whole number part of the mixed number.
- The remainder becomes the numerator of the proper fraction.
- The denominator remains the same.
For example, let's convert 17/5 back to a mixed number:
17 divided by 5 is 3 with a remainder of 2. Therefore, 17/5 = 3 2/5.
Practical Applications of Improper Fractions
Improper fractions find applications in various fields:
- Cooking and Baking: Precise measurements in recipes often involve improper fractions, ensuring accurate proportions of ingredients.
- Construction and Engineering: Detailed plans and blueprints frequently utilize improper fractions to represent dimensions and measurements.
- Finance: Calculating interest rates and proportions of investments might involve working with improper fractions.
- Science: Many scientific calculations, especially those dealing with measurements and ratios, necessitate the use of improper fractions.
- Computer Programming: Representing fractional values in computer programs may involve using improper fractions for accurate computations.
Advanced Concepts Related to Fractions
While this guide focuses on converting 4 1/2 to an improper fraction, several other important concepts relate to fractions:
- Simplifying Fractions: Reducing fractions to their lowest terms by finding the greatest common divisor of the numerator and denominator.
- Adding and Subtracting Fractions: Requires a common denominator.
- Multiplying and Dividing Fractions: Involves multiplying numerators and denominators, or inverting the second fraction and multiplying.
- Fractions and Decimals: Converting fractions to decimals and vice versa.
- Fractions and Percentages: Understanding the relationship between fractions, decimals, and percentages.
Conclusion
Converting 4 1/2 to the improper fraction 9/2 is a fundamental mathematical operation with wide-ranging applications. Mastering this conversion, along with understanding the broader context of fractions and related concepts, equips you with crucial skills for various academic and real-world scenarios. Remember the simple steps: multiply the whole number by the denominator, add the numerator, and keep the same denominator. Practice regularly, and you'll quickly become proficient in converting between mixed numbers and improper fractions. This skill is a cornerstone of mathematical fluency and essential for tackling more complex mathematical problems in the future. The ability to seamlessly work with fractions will enhance your problem-solving skills across numerous disciplines.
Latest Posts
Latest Posts
-
How Much Is 19 Celsius In Fahrenheit
Apr 03, 2025
-
What Are The Three Main Weapons Of Predators
Apr 03, 2025
-
How Many Phosphate Groups Does Atp Have
Apr 03, 2025
-
What Is 300 F In C
Apr 03, 2025
-
Convert From Rectangular To Polar Equation
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about 4 1/2 As An Improper Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
