4 3 As A Mixed Number
Kalali
Mar 31, 2025 · 5 min read
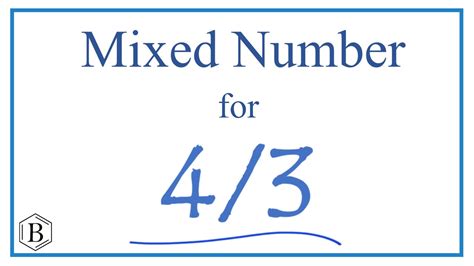
Table of Contents
4 3 as a Mixed Number: A Deep Dive into Fractions and Their Conversions
The seemingly simple expression "4 3" isn't a standard mathematical notation. It's likely meant to represent a mixed number, a number that combines a whole number and a fraction. However, the missing operator between the '4' and the '3' is crucial. We'll assume it's intended to represent the mixed number 4 3/x, where 'x' represents an unspecified denominator. This article will explore various possibilities, explain the process of converting between improper fractions and mixed numbers, and delve into the practical applications of understanding these concepts.
Understanding Mixed Numbers and Improper Fractions
Before we tackle the mystery of "4 3," let's solidify our understanding of the key concepts:
Mixed Numbers: These numbers combine a whole number and a proper fraction (where the numerator is smaller than the denominator). For example, 2 ¾, 5 ⅓, and 1 ⅛ are all mixed numbers. They represent a quantity greater than one but less than the next whole number.
Improper Fractions: In an improper fraction, the numerator is greater than or equal to the denominator. For instance, 11/4, 16/3, and 9/9 are improper fractions. They represent a quantity greater than or equal to one.
Converting Between Mixed Numbers and Improper Fractions:
The process of converting between these two forms is crucial for various mathematical operations.
Mixed Number to Improper Fraction:
- Multiply: Multiply the whole number by the denominator of the fraction.
- Add: Add the result from step 1 to the numerator of the fraction.
- Keep the Denominator: The denominator remains unchanged.
Let's illustrate with the example 2 ¾:
- Multiply: 2 * 4 = 8
- Add: 8 + 3 = 11
- Keep the Denominator: The denominator is 4.
Therefore, 2 ¾ is equivalent to the improper fraction 11/4.
Improper Fraction to Mixed Number:
- Divide: Divide the numerator by the denominator.
- Whole Number: The quotient is the whole number part of the mixed number.
- Remainder: The remainder is the numerator of the fractional part.
- Keep the Denominator: The denominator remains unchanged.
Let's convert 11/4 back to a mixed number:
- Divide: 11 ÷ 4 = 2 with a remainder of 3.
- Whole Number: The whole number is 2.
- Remainder: The remainder is 3.
- Keep the Denominator: The denominator is 4.
Therefore, 11/4 is equivalent to the mixed number 2 ¾.
Exploring Possible Interpretations of "4 3"
Since "4 3" lacks a clear operator, let's consider several possibilities, assuming it represents a mixed number:
Possibility 1: 4 3/1
If the '3' represents the numerator and an implied denominator of 1 is assumed, then:
- Improper Fraction: Following the conversion steps, this mixed number (4 3/1) translates to (4 * 1) + 3 / 1 = 7/1 = 7. This is simply the whole number 7.
Possibility 2: 4 3/2
If the denominator is 2, the mixed number is 4 3/2:
-
Improper Fraction: (4 * 2) + 3 / 2 = 11/2
-
Decimal Equivalent: 11/2 = 5.5
Possibility 3: 4 3/3
If the denominator is 3, the mixed number is 4 3/3:
-
Improper Fraction: (4 * 3) + 3 / 3 = 15/3
-
Simplified Fraction: 15/3 = 5 (This is a whole number)
Possibility 4: 4 3/4
If the denominator is 4, the mixed number is 4 3/4:
-
Improper Fraction: (4 * 4) + 3 / 4 = 19/4
-
Decimal Equivalent: 19/4 = 4.75
Possibility 5: 4 3/10
If the denominator is 10, the mixed number is 4 3/10:
-
Improper Fraction: (4 * 10) + 3 / 10 = 43/10
-
Decimal Equivalent: 43/10 = 4.3
Possibility 6: And so on...
The possibilities are endless. The interpretation of "4 3" depends entirely on the intended denominator. Without specifying the denominator, the expression is ambiguous.
Practical Applications of Mixed Numbers and Improper Fractions
Mixed numbers and improper fractions are fundamental concepts with widespread applications across various fields:
-
Cooking and Baking: Recipes often call for fractional amounts of ingredients. Understanding mixed numbers is crucial for accurate measurements.
-
Construction and Engineering: Precise measurements are vital in construction and engineering projects. Working with fractions ensures accuracy and prevents errors.
-
Finance: Calculating interest, discounts, and proportions often involves fractions and mixed numbers.
-
Data Analysis: Representing and manipulating data often involves fractions and their conversion to percentages or decimals.
-
Sewing and Tailoring: Precise measurements are necessary in the fashion industry. Understanding fractions and mixed numbers enables accurate pattern cutting and garment construction.
-
Computer Programming: Representing data and performing calculations within algorithms may involve fractional values.
-
Everyday Life: Many everyday scenarios involve dividing or sharing quantities, often requiring the understanding of fractions and mixed numbers. For example, dividing a pizza among friends, splitting a bill, or measuring ingredients for a recipe.
Beyond the Basics: Working with Mixed Numbers and Improper Fractions
Once you grasp the basic conversions, you can progress to more complex operations:
-
Adding and Subtracting Mixed Numbers: It's usually easier to convert mixed numbers to improper fractions before performing addition or subtraction. This simplifies the calculation and prevents errors.
-
Multiplying and Dividing Mixed Numbers: Again, converting to improper fractions before performing these operations simplifies the process.
-
Comparing Mixed Numbers: It's helpful to convert to improper fractions to easily compare the relative sizes of different mixed numbers.
-
Solving Equations: Many algebraic equations involve fractions and mixed numbers. Understanding these concepts is crucial for solving these equations.
Conclusion: The Importance of Clarity in Mathematical Notation
The ambiguity of "4 3" highlights the importance of clear and precise mathematical notation. Without a defined operator or context, the interpretation is subjective. Always ensure that mathematical expressions are unambiguous to avoid confusion and errors. The ability to confidently convert between mixed numbers and improper fractions is essential for success in mathematics and its many practical applications. Mastering this fundamental skill will empower you to tackle more complex mathematical problems with confidence and precision. Remember to always double-check your work and pay close attention to detail, ensuring that your calculations are accurate and your notations are clear and concise.
Latest Posts
Latest Posts
-
Describe The Main Parts Of A Proof
Apr 01, 2025
-
1 8 Of An Ounce Is How Many Grams
Apr 01, 2025
-
What Is 1 1 As A Fraction
Apr 01, 2025
-
What Percentage Is 3 Of 15
Apr 01, 2025
-
What Is 4 Over 3 As A Decimal
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about 4 3 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
