4 9 As A Mixed Number
Kalali
Apr 03, 2025 · 6 min read
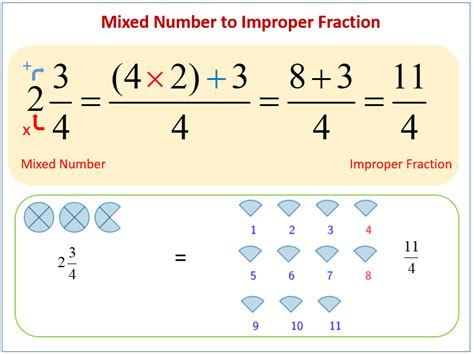
Table of Contents
4 9 as a Mixed Number: A Comprehensive Guide
Understanding fractions and mixed numbers is fundamental to mathematics. This comprehensive guide delves into the intricacies of representing the improper fraction 4/9 as a mixed number, exploring various methods and providing a solid foundation for further learning. We'll also touch upon the practical applications of mixed numbers and how understanding them can simplify calculations and problem-solving.
What is a Mixed Number?
A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator (the top number) is smaller than the denominator (the bottom number). For instance, 1 ¾, 2 ⅓, and 5 ⅛ are all examples of mixed numbers. They represent a quantity that's more than one whole unit but less than the next whole number.
Why Use Mixed Numbers?
Mixed numbers offer a more intuitive and practical way to represent quantities in many real-world scenarios. Imagine you have two and a half pizzas. Writing this as 5/2 (an improper fraction) is mathematically correct, but less understandable than 2 ½. Mixed numbers make it easier to visualize and comprehend quantities. This is particularly true when dealing with measurements, such as 3 ¼ inches or 1 ½ cups of flour.
Converting Improper Fractions to Mixed Numbers: The Core Concept
An improper fraction is a fraction where the numerator is greater than or equal to the denominator. 4/9, however, is not an improper fraction; it's a proper fraction. Therefore, it cannot be converted into a mixed number. A mixed number always involves a whole number component, and 4/9 is less than one whole.
Let's illustrate the conversion process with examples of improper fractions to demonstrate the concept clearly:
Example 1: Converting 7/4 to a Mixed Number
- Divide the numerator by the denominator: 7 ÷ 4 = 1 with a remainder of 3.
- The quotient (1) becomes the whole number part of the mixed number.
- The remainder (3) becomes the numerator of the fraction part.
- The denominator remains the same (4).
Therefore, 7/4 as a mixed number is 1 ¾.
Example 2: Converting 11/3 to a Mixed Number
- Divide the numerator by the denominator: 11 ÷ 3 = 3 with a remainder of 2.
- The quotient (3) is the whole number.
- The remainder (2) is the new numerator.
- The denominator stays the same (3).
Therefore, 11/3 as a mixed number is 3 ⅔.
Why 4/9 Cannot Be Expressed as a Mixed Number
As stated earlier, 4/9 is a proper fraction. The numerator (4) is smaller than the denominator (9). This means it represents a quantity less than one whole unit. There's no whole number component to include in a mixed number representation. Trying to divide 4 by 9 results in a decimal value (approximately 0.444), not a whole number and a remainder. Therefore, 4/9 remains as a proper fraction; it cannot be converted into a mixed number.
Working with Proper Fractions like 4/9
Although 4/9 cannot be expressed as a mixed number, we can still perform various mathematical operations with it. These include:
- Addition and Subtraction: Adding or subtracting fractions requires a common denominator. For instance, adding 4/9 and 2/9 results in 6/9, which can be simplified to 2/3.
- Multiplication: To multiply fractions, multiply the numerators together and the denominators together. For example, (4/9) * (2/3) = 8/27.
- Division: To divide fractions, invert the second fraction and multiply. For example, (4/9) ÷ (2/3) = (4/9) * (3/2) = 12/18 = 2/3.
Simplifying Fractions
Simplifying fractions is crucial for representing them in their most concise form. It involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. For example, the fraction 6/9 can be simplified by finding the GCD of 6 and 9, which is 3. Dividing both numerator and denominator by 3 gives us the simplified fraction 2/3.
Let’s take a look at a few different scenarios to solidify understanding:
Scenario 1: Adding fractions with the same denominator.
If we are asked to add 4/9 + 2/9, we simply add the numerators while keeping the denominator the same. 4 + 2 = 6, so the result is 6/9. We can simplify this fraction further by dividing both the numerator and denominator by their greatest common divisor, which is 3, to arrive at the simplest form: 2/3.
Scenario 2: Adding fractions with different denominators.
To add 4/9 and 1/3, we must first find a common denominator. The least common multiple of 9 and 3 is 9. We convert 1/3 to an equivalent fraction with a denominator of 9: 1/3 * 3/3 = 3/9. Now we can add: 4/9 + 3/9 = 7/9.
Scenario 3: Subtracting fractions.
Subtracting fractions follows the same principles as adding fractions. We must find a common denominator if needed and then subtract the numerators. For example, 4/9 - 1/3 = 4/9 - 3/9 = 1/9.
Scenario 4: Multiplication of fractions.
Multiplying fractions is straightforward. Multiply the numerators together and the denominators together. For example, (4/9) * (2/3) = 8/27.
Scenario 5: Division of fractions.
Dividing fractions involves inverting the second fraction and then multiplying. For example, (4/9) / (1/3) = (4/9) * (3/1) = 12/9 = 4/3. Remember to simplify if possible.
Practical Applications of Fractions and Mixed Numbers
Fractions and mixed numbers are essential in various real-world applications, including:
- Cooking and Baking: Recipes often require fractional measurements of ingredients, such as ½ cup of sugar or 1 ¼ teaspoons of baking powder.
- Construction and Engineering: Precise measurements are vital in these fields, and fractions and mixed numbers are used to represent dimensions and quantities.
- Finance: Fractions and percentages (which are essentially fractions) are used extensively in financial calculations, such as interest rates, profit margins, and stock prices.
- Science: Scientific measurements and calculations frequently involve fractions and mixed numbers.
Conclusion: Mastering Fractions and Mixed Numbers
While 4/9 itself remains a proper fraction and thus cannot be expressed as a mixed number, understanding the difference between proper and improper fractions, and the process of converting between them, is a vital mathematical skill. This article has provided a detailed explanation of this conversion process and highlighted the importance and practical applications of fractions and mixed numbers across various disciplines. Mastering these concepts will significantly enhance your mathematical abilities and problem-solving skills. Remember to always simplify your fractions to their lowest terms for the clearest and most accurate representation.
Latest Posts
Latest Posts
-
An Injured Limb Should Be Kept Above Heart Level
Apr 04, 2025
-
How Many Ounces Is 1 Cup Of Butter
Apr 04, 2025
-
Does My Brain Know I Have Eyes
Apr 04, 2025
-
Common Multiples Of 4 And 14
Apr 04, 2025
-
Does Weathering Affect Different Materials Differently
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about 4 9 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
