4 Over 9 As A Decimal
Kalali
Mar 30, 2025 · 5 min read
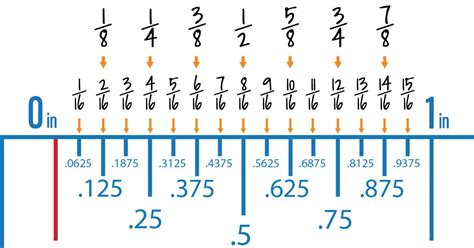
Table of Contents
4 Over 9 as a Decimal: A Comprehensive Guide
Converting fractions to decimals is a fundamental skill in mathematics with widespread applications in various fields. This article delves deep into the conversion of the fraction 4/9 into its decimal equivalent, exploring different methods, underlying concepts, and practical implications. We'll go beyond a simple answer, providing a thorough understanding of the process and its relevance.
Understanding Fractions and Decimals
Before diving into the conversion of 4/9, let's solidify our understanding of fractions and decimals.
Fractions represent parts of a whole. They consist of a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts we have, while the denominator indicates the total number of equal parts the whole is divided into.
Decimals, on the other hand, represent numbers based on the powers of 10. They use a decimal point to separate the whole number part from the fractional part. Each digit to the right of the decimal point represents a decreasing power of 10 (tenths, hundredths, thousandths, and so on).
Methods for Converting 4/9 to a Decimal
There are several ways to convert the fraction 4/9 to a decimal. We will explore the most common methods:
Method 1: Long Division
This is the most straightforward method. We divide the numerator (4) by the denominator (9):
0.444...
9 | 4.000
-3.6
0.40
-0.36
0.040
-0.036
0.004...
As you can see, the division process continues indefinitely, yielding a repeating decimal. The digit 4 repeats infinitely. We represent this repeating decimal using a bar over the repeating digit: 0.4̅
Method 2: Using Equivalent Fractions
While this method isn't as direct for 4/9, it's valuable for understanding the relationship between fractions and decimals. We can't easily find an equivalent fraction with a denominator that's a power of 10 (like 10, 100, 1000, etc.) for 4/9. This is because 9's prime factorization is only 3 x 3, and it doesn't share any prime factors with 10 (2 x 5). However, this method highlights why some fractions result in terminating decimals and others in repeating decimals.
Method 3: Understanding Repeating Decimals
The result of converting 4/9 to a decimal is a repeating decimal, specifically 0.4̅. Understanding repeating decimals is crucial. A repeating decimal is a decimal number that has a sequence of digits that repeats indefinitely. These repeating sequences are often represented with a bar over the repeating digits. For example, 1/3 = 0.3̅, 2/3 = 0.6̅, and so on.
The Significance of Repeating Decimals
The fact that 4/9 results in a repeating decimal is not a coincidence. It's directly related to the relationship between the numerator and the denominator of the fraction. If the denominator of a fraction in its simplest form contains prime factors other than 2 and 5, the decimal representation will be a repeating decimal. Since 9 = 3 x 3, it contains a prime factor (3) other than 2 and 5, resulting in the repeating decimal 0.4̅.
Practical Applications of 4/9 as a Decimal
The decimal equivalent of 4/9, 0.4̅, finds application in various scenarios:
-
Calculating Percentages: If you need to calculate 4/9 of a quantity, you can use 0.4̅ as a decimal multiplier. For example, 4/9 of 100 is 100 * 0.4̅ ≈ 44.44.
-
Measurement and Engineering: In fields like engineering and construction, precise measurements are crucial. Converting fractions to decimals can facilitate calculations and comparisons.
-
Financial Calculations: In financial calculations, especially those involving interest rates or proportions of investments, using decimal representations simplifies calculations.
Beyond 4/9: Generalizing the Conversion Process
The conversion process for 4/9 can be generalized to other fractions. The key is to understand the relationship between the denominator and the resulting decimal:
-
Denominators with only 2 and 5 as prime factors: These fractions will always result in terminating decimals (decimals that end). Examples: 1/2 = 0.5, 3/4 = 0.75, 7/20 = 0.35.
-
Denominators with prime factors other than 2 and 5: These fractions will almost always result in repeating decimals. Examples: 1/3 = 0.3̅, 1/7 = 0.142857̅, 2/9 = 0.2̅.
Rounding Repeating Decimals
In practical applications, we often need to round repeating decimals to a specific number of decimal places. Rounding 0.4̅ to two decimal places gives us 0.44. Rounding to three decimal places gives us 0.444, and so on. The accuracy of the rounded decimal depends on the context and the required level of precision.
Error Introduced by Rounding
It's important to acknowledge that rounding a repeating decimal introduces a small amount of error. The more decimal places you use, the smaller the error becomes. However, there will always be a small discrepancy between the exact value (0.4̅) and the rounded value (e.g., 0.44 or 0.444). Understanding this error is crucial in applications where high precision is needed.
Using Calculators and Software for Conversions
Most scientific calculators and mathematical software packages can perform fraction-to-decimal conversions accurately. These tools can handle repeating decimals effectively, often displaying them with the appropriate notation (like 0.4̅) or providing options for rounding to a specified number of decimal places.
Conclusion: Mastering Fraction to Decimal Conversions
Converting fractions to decimals, especially repeating decimals like 4/9 = 0.4̅, is a fundamental mathematical skill with broad applicability. By understanding the methods involved, the significance of repeating decimals, and the potential for rounding errors, you can confidently perform these conversions and apply them to various real-world scenarios. Remember to choose the method that best suits your needs and always consider the required level of precision for your application. The ability to accurately convert fractions to decimals is a cornerstone of numeracy, enabling efficient problem-solving in numerous fields.
Latest Posts
Latest Posts
-
How Many Inches Is 128 Cm
Apr 01, 2025
-
Cuanto Es 63 Pulgadas En Pies
Apr 01, 2025
-
What Percentage Is 35 Out Of 50
Apr 01, 2025
-
How To Make A Velocity Vs Time Graph
Apr 01, 2025
-
Is The Atlantic Colder Than The Pacific
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about 4 Over 9 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
