4 Right Angles And 2 Pairs Of Parallel Sides
Kalali
Mar 31, 2025 · 6 min read
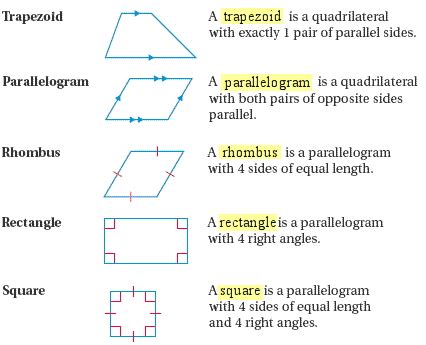
Table of Contents
4 Right Angles and 2 Pairs of Parallel Sides: Delving into the World of Rectangles
The seemingly simple statement, "4 right angles and 2 pairs of parallel sides," instantly evokes a familiar geometric shape: the rectangle. While seemingly basic, the rectangle holds a significant place in geometry, mathematics, and even our everyday lives. This article will delve deep into the fascinating world of rectangles, exploring their properties, applications, and significance within broader mathematical concepts. We'll explore various aspects, from their fundamental definitions to advanced geometrical theorems related to them.
Understanding the Definition: What Makes a Rectangle a Rectangle?
A rectangle, at its core, is a quadrilateral – a four-sided polygon. However, it's not just any quadrilateral; it possesses specific, defining characteristics. These characteristics are precisely what distinguish it from other quadrilaterals like squares, parallelograms, and trapezoids. The crucial defining features are:
- Four Right Angles: Each of the four interior angles of a rectangle measures exactly 90 degrees. This is a cornerstone property. Without these right angles, the shape isn't a rectangle.
- Two Pairs of Parallel Sides: The opposite sides of a rectangle are parallel to each other. This parallelism ensures that the shape is stable and maintains its rectangular form.
These two properties are interdependent. The existence of four right angles inherently implies the existence of two pairs of parallel sides, and vice versa, given the context of a quadrilateral. This interdependency forms the elegant and concise definition of a rectangle.
Distinguishing Rectangles from other Quadrilaterals
Understanding the nuances that differentiate a rectangle from other quadrilaterals is vital. Let's examine the key distinctions:
Rectangle vs. Square:
A square is a special type of rectangle. It satisfies all the properties of a rectangle – four right angles and two pairs of parallel sides. The crucial difference lies in the lengths of its sides. In a square, all four sides are equal in length. A rectangle, however, only requires opposite sides to be equal in length.
Rectangle vs. Parallelogram:
A parallelogram is a quadrilateral with two pairs of parallel sides. However, its angles are not necessarily right angles. Rectangles are a subset of parallelograms; all rectangles are parallelograms, but not all parallelograms are rectangles.
Rectangle vs. Trapezoid:
A trapezoid is a quadrilateral with only one pair of parallel sides. This immediately distinguishes it from a rectangle, which requires two pairs of parallel sides.
Exploring Properties of Rectangles: Beyond the Basics
The defining properties of a rectangle form the foundation for numerous other inherent characteristics. Let's explore some of these crucial properties:
- Opposite Sides are Equal: As mentioned, the opposite sides of a rectangle are equal in length. This is a direct consequence of the parallel sides and right angles.
- Diagonals Bisect Each Other: The diagonals of a rectangle (lines connecting opposite corners) intersect at their midpoints. This means they divide each other into two equal segments.
- Diagonals are Equal in Length: Unlike other parallelograms, the diagonals of a rectangle are equal in length. This is another significant characteristic.
- Area Calculation: The area of a rectangle is calculated by multiplying its length and width: Area = Length × Width. This simple formula is widely used in various applications.
- Perimeter Calculation: The perimeter of a rectangle is the sum of all its sides: Perimeter = 2 × (Length + Width). This is essential for determining the total length of the boundary.
Rectangles in Action: Real-World Applications
Rectangles are ubiquitous in our everyday lives. Their simple yet stable geometry makes them ideal for countless applications:
- Architecture and Construction: Buildings, rooms, windows, and doors are often rectangular. The stability and ease of construction associated with rectangles make them a preferred choice in architecture.
- Everyday Objects: Many everyday objects, from books and screens to tables and posters, are rectangular in shape.
- Art and Design: Rectangles play a significant role in art and design, forming the basis of many compositions and layouts. The balanced proportions of a rectangle offer a sense of order and harmony.
- Computer Graphics and Programming: Rectangles form the foundation of many computer graphics and programming concepts, such as bounding boxes and image representation.
- Agriculture and Land Surveying: Rectangular plots of land are commonly used in agriculture and land surveying due to their ease of measurement and division.
Geometric Theorems and Rectangles: Deeper Exploration
Several geometric theorems and concepts directly relate to rectangles. Understanding these connections expands our comprehension of their mathematical significance:
- Pythagorean Theorem: The Pythagorean theorem, a cornerstone of geometry, applies to right-angled triangles, which are integral components of rectangles. The theorem states that in a right-angled triangle, the square of the hypotenuse (the longest side) is equal to the sum of the squares of the other two sides. This theorem is frequently used in calculations involving rectangles, particularly when dealing with diagonals.
- Similar Rectangles: Two rectangles are considered similar if their corresponding angles are equal and their corresponding sides are proportional. Similar rectangles maintain the same shape but differ in size.
- Congruent Rectangles: Two rectangles are congruent if they have the same size and shape. This means all corresponding sides and angles are equal.
Advanced Concepts and Related Shapes
Beyond the fundamental properties, the concept of rectangles extends into more advanced mathematical areas:
- Rectangular Coordinates: Rectangular coordinates, also known as Cartesian coordinates, use horizontal and vertical lines (essentially forming a grid of rectangles) to pinpoint locations on a plane. This system is crucial in various fields, including mathematics, physics, and computer graphics.
- Rectangular Prisms: Extending into three dimensions, we find rectangular prisms (box-like shapes). These shapes retain the essence of the rectangle, possessing rectangular faces.
- Higher Dimensions: The concept of rectangles can be generalized to higher dimensions, leading to hyperrectangles (or n-dimensional rectangles). These are complex mathematical constructs, but they demonstrate the fundamental power and adaptability of the concept.
Conclusion: The Enduring Importance of Rectangles
The humble rectangle, with its four right angles and two pairs of parallel sides, transcends its seemingly simple definition. Its presence in geometry, mathematics, and our daily lives is undeniable. From basic area calculations to advanced mathematical concepts and real-world applications, rectangles form an essential part of our understanding of shapes, space, and the world around us. This article has only scratched the surface of the rich mathematical landscape associated with rectangles. Further exploration will only reveal more fascinating aspects and applications of this fundamental geometric shape. Its enduring importance lies not just in its simplicity but also in its far-reaching implications across numerous fields of study and practical applications. The rectangle, a testament to the beauty and power of fundamental geometric principles, continues to shape our world in countless ways.
Latest Posts
Latest Posts
-
What Is The Percent Of 20 Out Of 25
Apr 02, 2025
-
Where Is The North Magnetic Pole Of This Current Loop
Apr 02, 2025
-
Magnesium Metal Or Nonmetal Or Metalloid
Apr 02, 2025
-
How Many Ounces Are In 125 Ml
Apr 02, 2025
-
What Is 10 Out Of 15
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about 4 Right Angles And 2 Pairs Of Parallel Sides . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
