4 To The Power Of 1
Kalali
Apr 02, 2025 · 6 min read
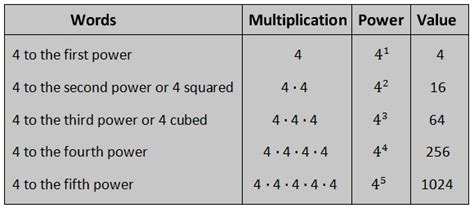
Table of Contents
4 to the Power of 1: A Deep Dive into Exponents and Their Applications
The seemingly simple mathematical expression, 4 to the power of 1 (or 4¹), offers a fascinating gateway into the broader world of exponents, their properties, and their wide-ranging applications across various fields. While the answer itself is straightforward – 4 – the underlying concepts hold significant weight in mathematics, computer science, finance, and beyond. This article will delve deep into the meaning of 4¹, explore the fundamental principles of exponents, and demonstrate their practical relevance through real-world examples.
Understanding Exponents: A Foundation
Before we fully unravel the mystery of 4¹, let's establish a solid understanding of exponents. An exponent, also known as a power or index, indicates how many times a number (the base) is multiplied by itself. The general form is expressed as bⁿ, where 'b' represents the base and 'n' represents the exponent.
For instance:
- 2³ = 2 x 2 x 2 = 8 (2 is the base, 3 is the exponent)
- 5² = 5 x 5 = 25 (5 is the base, 2 is the exponent)
- 10¹ = 10 (10 is the base, 1 is the exponent)
In our case, 4¹ signifies that the base, 4, is multiplied by itself only once. Therefore, 4¹ = 4. This might appear trivial, but it's crucial for grasping the underlying rules governing exponents.
Key Properties of Exponents
Understanding the following properties is vital for working with exponents effectively:
-
Product of Powers: When multiplying two numbers with the same base, add the exponents: bᵐ x bⁿ = bᵐ⁺ⁿ. For example, 2² x 2³ = 2⁵ = 32.
-
Quotient of Powers: When dividing two numbers with the same base, subtract the exponents: bᵐ / bⁿ = bᵐ⁻ⁿ. For example, 3⁴ / 3² = 3² = 9.
-
Power of a Power: When raising a power to another power, multiply the exponents: (bᵐ)ⁿ = bᵐⁿ. For example, (2²)³ = 2⁶ = 64.
-
Power of a Product: When raising a product to a power, raise each factor to that power: (b x c)ⁿ = bⁿ x cⁿ. For example, (2 x 3)² = 2² x 3² = 4 x 9 = 36.
-
Power of a Quotient: When raising a quotient to a power, raise both the numerator and the denominator to that power: (b/c)ⁿ = bⁿ/cⁿ. For example, (2/3)² = 2²/3² = 4/9.
-
Zero Exponent: Any non-zero base raised to the power of zero equals 1: b⁰ = 1. For example, 5⁰ = 1.
-
Negative Exponent: A negative exponent indicates the reciprocal of the base raised to the positive exponent: b⁻ⁿ = 1/bⁿ. For example, 2⁻² = 1/2² = 1/4.
These properties are fundamental to solving more complex exponential equations and manipulating exponential expressions. Even the seemingly simple 4¹ relies on these underlying rules.
The Significance of 4¹ and the Identity Property
The fact that 4¹ equals 4 highlights the identity property of multiplication. This property states that any number multiplied by 1 remains unchanged. In the context of exponents, this means that raising any base to the power of 1 results in the base itself. This is a cornerstone of exponential arithmetic, and understanding it clarifies many other exponential concepts.
Think of it this way: 4¹ represents a single instance of the number 4. There's no repetition or multiplication involved beyond the number itself. This simplicity underscores the importance of the exponent '1' as a foundational element within the broader system of exponents.
Applications of Exponents: Beyond the Basics
While 4¹ might seem elementary, the principles behind it are applied extensively across various disciplines:
1. Computer Science: Binary Numbers and Data Representation
Computers operate using binary code, a system based on two digits: 0 and 1. These binary digits (bits) are fundamental to representing information in digital form. Exponents play a crucial role in understanding how large numbers are represented in binary. For instance, the binary number 1011 can be converted to decimal form using powers of 2:
1 x 2³ + 0 x 2² + 1 x 2¹ + 1 x 2⁰ = 8 + 0 + 2 + 1 = 11
Here, powers of 2 are used to determine the decimal equivalent. Understanding exponents is essential for working with binary and other number systems used in computer science.
2. Finance: Compound Interest and Growth
Exponents are fundamental to calculating compound interest, a critical concept in finance. Compound interest is interest earned not only on the principal amount but also on accumulated interest. The formula for compound interest is:
A = P (1 + r/n)^(nt)
Where:
- A = the future value of the investment/loan, including interest
- P = the principal investment amount (the initial deposit or loan amount)
- r = the annual interest rate (decimal)
- n = the number of times that interest is compounded per year
- t = the number of years the money is invested or borrowed for
The exponent (nt) determines the effect of compounding over time. A higher exponent (longer investment period) leads to significantly greater growth due to the power of compounding. Understanding exponential growth is vital for making informed financial decisions.
3. Biology: Population Growth and Decay
Exponential functions are used to model population growth (or decay) in biological systems. The growth of a bacterial colony, for example, can often be approximated using an exponential model. The exponent represents the number of generations, and the base represents the growth factor. Similarly, exponential decay models describe processes like radioactive decay.
4. Physics: Radioactive Decay and Exponential Attenuation
In physics, exponential functions describe radioactive decay, where the amount of a radioactive substance decreases over time. The decay constant is an exponent in the decay formula, determining the rate of decay. Similarly, exponential attenuation describes the decrease in intensity of a signal or radiation as it passes through a material.
5. Engineering: Signal Processing and Amplifier Gain
In electrical engineering, exponents are essential in describing amplifier gain and signal processing. Amplifier gain is often expressed in decibels (dB), which use logarithmic scales, and logarithmic and exponential functions are inverses of each other.
Beyond 4¹: Exploring More Complex Exponential Equations
While 4¹ provides a simple starting point, understanding exponents allows us to tackle more complex equations and scenarios. Consider the following examples:
-
Solving for the exponent: If we have the equation x³ = 64, we need to find the value of x. This requires finding the cube root of 64, which is 4 (because 4 x 4 x 4 = 64).
-
Solving for the base: If we have the equation 2ˣ = 16, we need to determine the value of x. In this case, x = 4 (because 2 x 2 x 2 x 2 = 16).
-
Solving equations involving multiple exponents: Equations like 3ˣ + 2ˣ = 10 may require iterative methods or logarithms to solve.
Mastering exponents unlocks the ability to tackle these more advanced mathematical problems.
Conclusion: The Unsung Power of 4¹
Although 4¹ might seem inconsequential at first glance, it acts as a fundamental building block in the vast landscape of exponential mathematics. Its simplicity masks the profound implications of exponents in various scientific, technological, and financial applications. Understanding the core principles of exponents, including the properties discussed above, empowers individuals to grapple with complex mathematical problems and to interpret and utilize exponential models in a diverse range of fields. The seemingly straightforward calculation of 4¹ thus serves as a key to unlocking a world of complex and powerful mathematical concepts. From understanding binary code to predicting population growth, the implications of exponents extend far beyond the simple arithmetic of raising a number to a power.
Latest Posts
Latest Posts
-
600 Mg Is How Many Grams
Apr 03, 2025
-
How Many Ounces Sour Cream In A Cup
Apr 03, 2025
-
Cuantos Grados Farenheit Son 180 Centigrados
Apr 03, 2025
-
How To Find Coordination Number Of Unit Cell
Apr 03, 2025
-
What Are Same Side Interior Angles
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about 4 To The Power Of 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
