45 Is 30 Of What Number
Kalali
Apr 12, 2025 · 5 min read
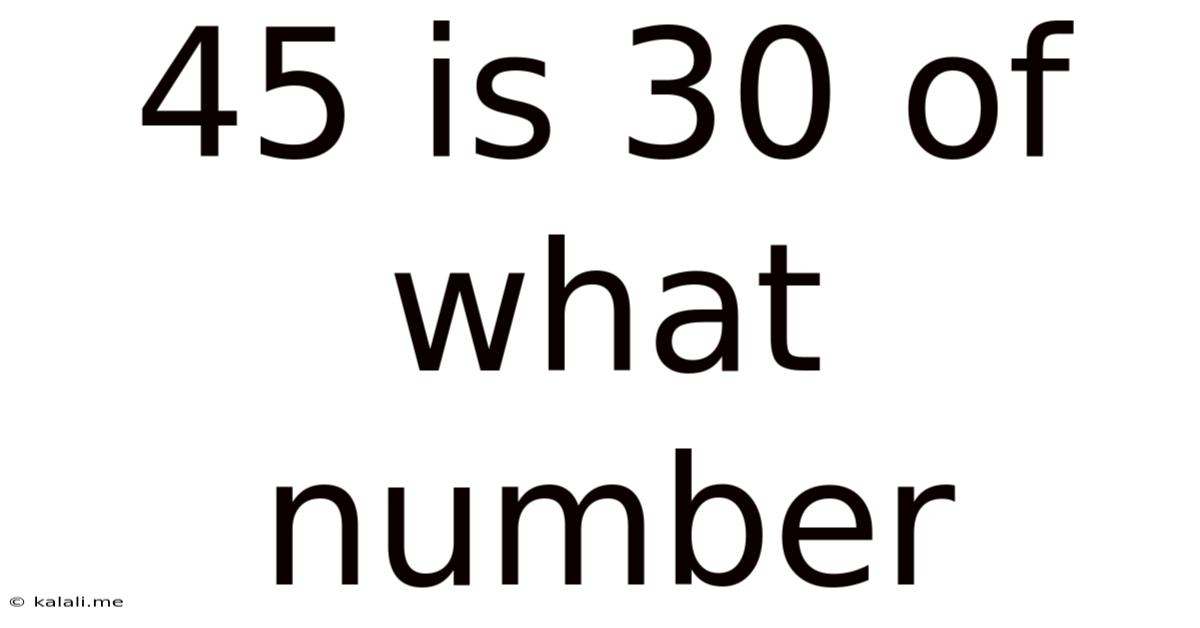
Table of Contents
45 is 30% of What Number? Unlocking the Power of Percentages
This seemingly simple question – "45 is 30% of what number?" – underpins a fundamental concept in mathematics with broad applications in various fields, from finance and budgeting to data analysis and scientific research. Understanding how to solve this type of problem is crucial for anyone aiming to improve their numerical literacy and problem-solving skills. This comprehensive guide will not only provide you with the solution but also delve into the underlying principles, offer multiple approaches to solving the problem, and explore practical examples to solidify your understanding.
Meta Description: Learn how to solve the percentage problem "45 is 30% of what number?" This comprehensive guide explains multiple approaches, provides practical examples, and explores the broader applications of percentage calculations.
Understanding the Fundamentals: Percentages and Proportions
Before diving into the solution, let's refresh our understanding of percentages and their relationship to proportions. A percentage is simply a fraction expressed as a part of 100. For instance, 30% can be written as 30/100 or 0.3. The problem "45 is 30% of what number?" can be rephrased as a proportion:
45 / x = 30 / 100
Where 'x' represents the unknown number we are trying to find. This equation states that 45 is to x as 30 is to 100. Solving for 'x' will give us the answer.
Method 1: Using the Proportion Equation
This is arguably the most straightforward method. We start with our proportion:
45 / x = 30 / 100
To solve for x, we can cross-multiply:
45 * 100 = 30 * x
This simplifies to:
4500 = 30x
Now, we isolate x by dividing both sides of the equation by 30:
x = 4500 / 30
x = 150
Therefore, 45 is 30% of 150.
Method 2: Converting Percentage to Decimal
Another common approach involves converting the percentage to its decimal equivalent. We know that 30% is equal to 0.3. We can then rewrite the problem as:
45 = 0.3 * x
To solve for x, we divide both sides by 0.3:
x = 45 / 0.3
x = 150
This method yields the same result: 45 is 30% of 150.
Method 3: Using the Formula: Part = Percentage × Whole
This method uses a fundamental formula for percentage calculations:
Part = Percentage × Whole
In our problem:
- Part = 45
- Percentage = 30% = 0.3
- Whole = x (the unknown number)
Substituting these values into the formula, we get:
45 = 0.3 * x
Solving for x, as shown in Method 2, gives us x = 150.
Practical Applications and Real-World Examples
The ability to solve percentage problems like this one has numerous practical applications in everyday life and various professional settings. Here are a few examples:
-
Finance: Calculating discounts, interest rates, taxes, and profit margins all involve percentage calculations. For example, if a store offers a 30% discount on an item originally priced at $150, you can use this method to quickly determine the discount amount ($45) and the final price ($105). Similarly, understanding compound interest requires proficiency in percentage calculations.
-
Data Analysis: Percentages are frequently used to represent proportions and trends in data. For example, if 45 out of 150 survey respondents answered "yes" to a particular question, this represents 30%. Understanding this percentage helps in drawing conclusions and making informed decisions based on the data.
-
Science: Many scientific calculations involve percentages, particularly when dealing with concentrations, yields, and error analysis. For instance, determining the percentage yield of a chemical reaction or the concentration of a solution requires these fundamental calculations.
-
Business: Businesses use percentage calculations for various purposes, including analyzing sales figures, tracking customer retention rates, and projecting future revenue. Understanding the percentage of sales growth or decline is crucial for strategic business planning.
-
Everyday Budgeting: Calculating tips, estimating the percentage of your income to allocate to different expenses, or determining the percentage increase in the price of goods and services are common everyday tasks that rely on this skill.
Expanding the Concept: Variations and Extensions
While this article focused on the specific problem "45 is 30% of what number?", the principles discussed are applicable to a wide range of percentage problems. Here are some variations:
-
Finding the percentage: If you know the part and the whole, you can calculate the percentage. For example: What percentage of 150 is 45? (Answer: 30%)
-
Finding the part: If you know the percentage and the whole, you can calculate the part. For example: What is 30% of 150? (Answer: 45)
-
Complex percentage problems: More complex problems may involve multiple percentages or require multiple steps to solve. For example, calculating the final price after multiple discounts or determining the percentage increase after several consecutive increases.
Mastering Percentage Calculations: Tips and Practice
Mastering percentage calculations requires practice and understanding the underlying principles. Here are some tips to improve your skills:
-
Practice regularly: Solve various percentage problems to build your confidence and proficiency.
-
Understand the concepts: Focus on understanding the relationships between percentages, fractions, and decimals.
-
Use multiple methods: Try different approaches to solve problems, as this can help you develop a deeper understanding of the concepts involved.
-
Check your answers: Always double-check your calculations to ensure accuracy.
-
Utilize online resources: Numerous online resources, including calculators and tutorials, can help you practice and improve your skills.
By understanding the methods presented in this article and practicing regularly, you'll not only be able to solve problems like "45 is 30% of what number?" but also confidently tackle more complex percentage calculations in various real-world scenarios. Remember, mastering percentages is a valuable skill that enhances your numerical literacy and problem-solving abilities across diverse fields.
Latest Posts
Latest Posts
-
How Many Hours Is 148 Minutes
Apr 18, 2025
-
What Percentage Of 18 Is 3
Apr 18, 2025
-
What Is 1 Out Of 6 As A Percentage
Apr 18, 2025
-
How Many Inches Is 20 Meters
Apr 18, 2025
-
54 Is What Percent Of 60
Apr 18, 2025
Related Post
Thank you for visiting our website which covers about 45 Is 30 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.