45 Is What Percent Of 50
Kalali
Apr 09, 2025 · 4 min read
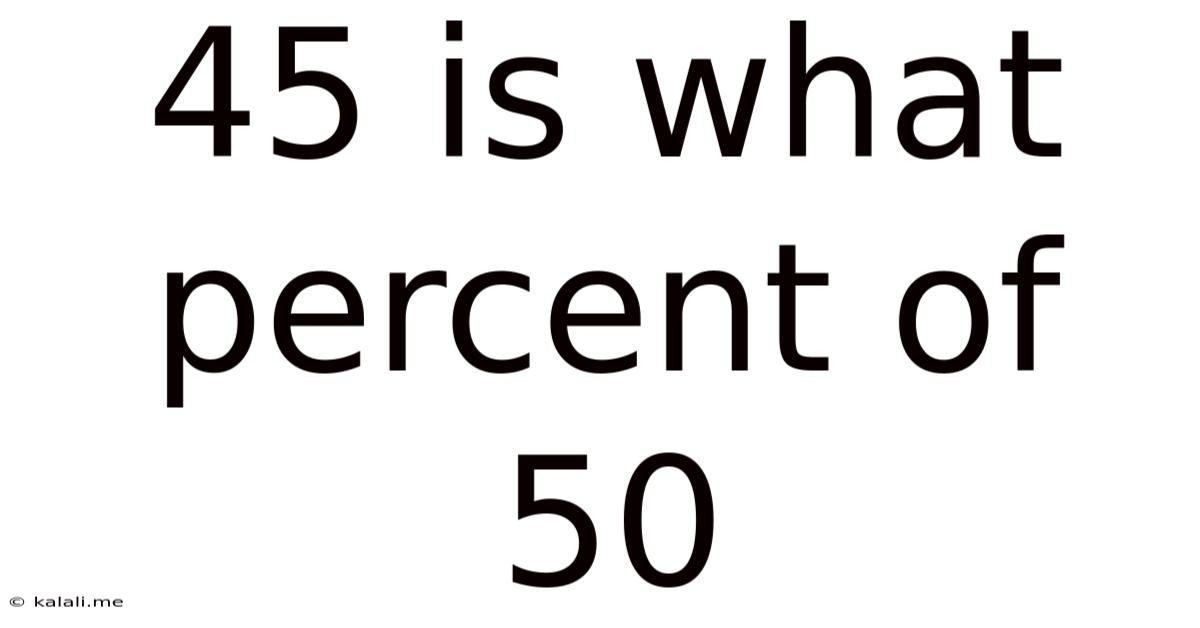
Table of Contents
45 is What Percent of 50? A Comprehensive Guide to Percentage Calculations
This seemingly simple question, "45 is what percent of 50?", unlocks a fundamental concept in mathematics with wide-ranging applications in everyday life, from calculating discounts and tax rates to understanding statistics and financial reports. This article will delve into the solution, exploring various methods for calculating percentages, explaining the underlying principles, and providing practical examples to solidify your understanding. We'll also look at how to solve similar problems and touch upon the importance of percentage calculations in various fields.
Understanding Percentages: The Basics
A percentage is simply a fraction expressed as a portion of 100. The word "percent" itself means "per hundred." Therefore, 1% represents 1/100, 10% represents 10/100 (or 1/10), and so on. Calculating percentages involves finding the relative proportion of one number to another, scaled to a base of 100. This scaling allows for easy comparison of different ratios.
Method 1: Using the Percentage Formula
The most straightforward approach to solving "45 is what percent of 50?" involves using the basic percentage formula:
(Part / Whole) x 100% = Percentage
In this case:
- Part: 45 (the value we're comparing)
- Whole: 50 (the total value)
Substituting these values into the formula, we get:
(45 / 50) x 100% = 90%
Therefore, 45 is 90% of 50.
Method 2: Setting up a Proportion
Another effective method involves setting up a proportion. We can represent the problem as:
45/50 = x/100
Here, 'x' represents the unknown percentage. To solve for 'x', we cross-multiply:
45 * 100 = 50 * x
4500 = 50x
x = 4500 / 50
x = 90
Again, we find that 45 is 90% of 50. This method is particularly useful for visualizing the relationship between the parts and the whole.
Method 3: Using Decimal Conversion
We can also solve this problem by converting the fraction to a decimal and then multiplying by 100%.
First, express the relationship as a fraction: 45/50
Then, divide 45 by 50: 45 ÷ 50 = 0.9
Finally, multiply the decimal by 100% to express it as a percentage: 0.9 x 100% = 90%
This method emphasizes the connection between decimals and percentages, highlighting that a percentage is simply a decimal multiplied by 100.
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial in numerous real-world scenarios. Here are some examples:
-
Discounts: A store offers a 20% discount on an item priced at $100. The discount amount is (20/100) * $100 = $20, and the final price is $80.
-
Taxes: A sales tax of 6% is applied to a purchase of $50. The tax amount is (6/100) * $50 = $3, and the total cost is $53.
-
Interest Rates: A savings account earns 3% interest annually on a balance of $1000. The interest earned in one year is (3/100) * $1000 = $30.
-
Grade Calculations: A student scores 45 out of 50 on a test. Their percentage score is (45/50) x 100% = 90%.
-
Data Analysis: Percentage changes are frequently used in data analysis to illustrate growth or decline in various metrics (e.g., sales, profits, website traffic). For example, if sales increased from 100 to 120 units, the percentage increase is [(120-100)/100] x 100% = 20%.
-
Financial Statements: Financial reports often use percentages to present key financial ratios, providing insights into a company's profitability, liquidity, and solvency.
-
Surveys and Polls: Results from surveys and polls are frequently presented as percentages to show the proportion of respondents who hold particular views or opinions.
Solving Similar Problems: Variations and Extensions
The principles discussed above can be applied to solve a range of percentage-related problems. For instance, you might encounter questions like:
- What is 25% of 80? (Answer: (25/100) * 80 = 20)
- 15 is what percent of 60? (Answer: (15/60) * 100% = 25%)
- 70 is 35% of what number? (This requires rearranging the formula: Whole = (Part / Percentage) x 100. Answer: (70 / 35) x 100 = 200)
These variations illustrate the adaptability of the percentage formula and the importance of understanding the relationship between the part, the whole, and the percentage.
Advanced Percentage Calculations: Compounding and More
While the examples above focus on simple percentage calculations, there are more complex scenarios involving compounding percentages, percentage increase/decrease over multiple periods, and other nuanced situations. Understanding these more advanced applications requires a deeper understanding of mathematical concepts but builds upon the fundamental principles discussed here. For example, compound interest calculations involve applying interest not only to the principal amount but also to the accumulated interest from previous periods.
Conclusion: Mastering Percentages for Success
The ability to calculate and interpret percentages is a vital skill across various disciplines and everyday situations. This article has explored different methods for solving percentage problems, showcasing their practical relevance and highlighting their role in diverse applications. By mastering these fundamental techniques, you can enhance your numerical literacy, improve your problem-solving capabilities, and gain a deeper understanding of the world around you. The seemingly simple question "45 is what percent of 50?" opens the door to a wider world of mathematical applications, empowering you to tackle more complex challenges and make informed decisions in various aspects of your life. Remember to practice regularly to reinforce your understanding and build confidence in your ability to perform these calculations accurately and efficiently.
Latest Posts
Related Post
Thank you for visiting our website which covers about 45 Is What Percent Of 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.