5 Is What Percent Of 50
Kalali
Apr 15, 2025 · 5 min read
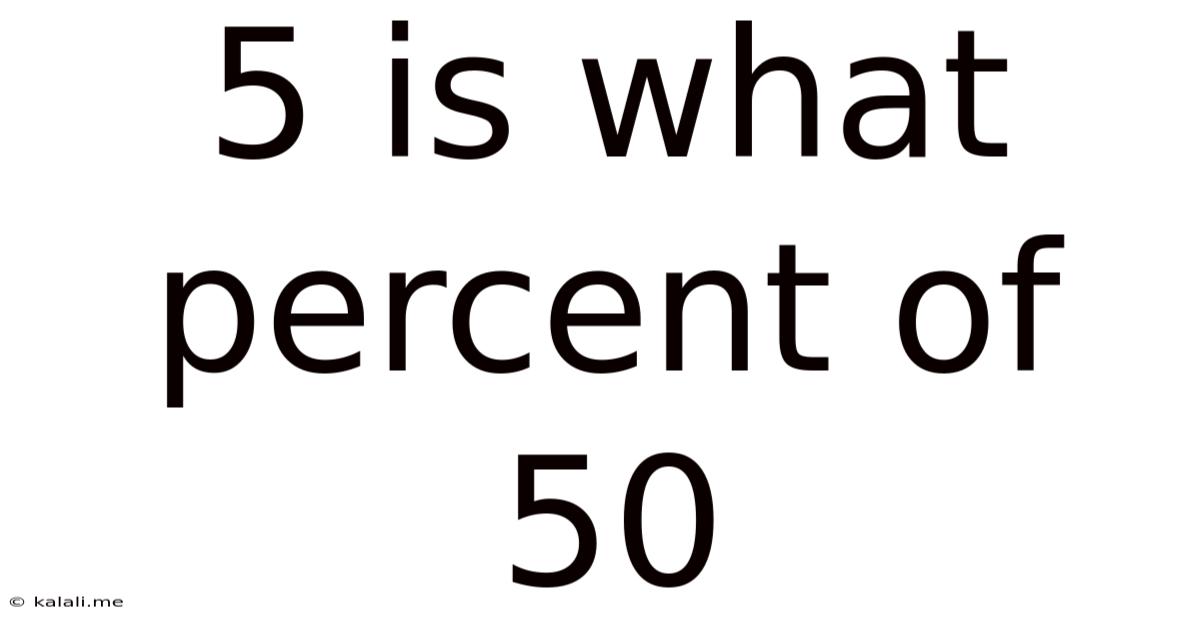
Table of Contents
5 is What Percent of 50? A Deep Dive into Percentages and Their Applications
This seemingly simple question, "5 is what percent of 50?", opens the door to a broader understanding of percentages, their calculation, and their widespread applications in various fields. This article will not only answer the question directly but also delve into the underlying mathematical principles, explore different methods of solving percentage problems, and demonstrate the practical relevance of percentages in everyday life and professional contexts. Understanding percentages is crucial for budgeting, analyzing data, interpreting statistics, and making informed decisions across numerous disciplines.
Meta Description: Learn how to calculate percentages with a step-by-step guide solving "5 is what percent of 50?". Explore different methods, real-world applications, and the importance of percentage understanding in various fields.
Understanding the Fundamentals of Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" is derived from the Latin phrase "per centum," meaning "out of a hundred." Therefore, a percentage represents a portion or proportion of a whole, expressed as a number followed by the "%" symbol. For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5 as a decimal.
Method 1: Using the Percentage Formula
The most straightforward method to solve "5 is what percent of 50?" involves using the basic percentage formula:
(Part / Whole) * 100 = Percentage
In this case:
- Part: 5 (the number we want to express as a percentage)
- Whole: 50 (the total or base number)
Substituting these values into the formula:
(5 / 50) * 100 = 10%
Therefore, 5 is 10% of 50.
Method 2: Setting up a Proportion
Another approach is to set up a proportion. A proportion is an equation stating that two ratios are equal. We can express the problem as:
5 / 50 = x / 100
Where 'x' represents the unknown percentage. To solve for 'x', we cross-multiply:
5 * 100 = 50 * x
500 = 50x
x = 500 / 50
x = 10
Therefore, x = 10%, confirming our previous result. This method is particularly useful when dealing with more complex percentage problems.
Method 3: Using Decimal Equivalents
We can also solve this using decimal equivalents. First, express the part as a fraction of the whole:
5 / 50 = 0.1
Then, convert the decimal to a percentage by multiplying by 100:
0.1 * 100 = 10%
This method highlights the direct relationship between decimals and percentages, offering a concise calculation approach.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is essential in numerous everyday situations and professional fields. Here are some examples:
-
Finance: Calculating interest rates on loans, savings accounts, and investments; determining discounts and sales tax; analyzing financial statements and budgets. Understanding percentage changes in stock prices, inflation rates, and economic growth is crucial for financial planning and investment decisions.
-
Retail: Calculating discounts and markups on products; determining profit margins; analyzing sales data and trends. Retailers rely heavily on percentage calculations for pricing strategies, inventory management, and sales forecasting.
-
Science: Expressing experimental results and statistical data; calculating error margins and uncertainties; representing proportions and ratios in scientific studies. Percentage calculations are fundamental in data analysis and interpretation across various scientific disciplines.
-
Education: Calculating grades and scores; evaluating student performance; representing statistical data related to academic achievement. Teachers and educators utilize percentages to assess student progress and identify areas for improvement.
-
Healthcare: Calculating medication dosages; determining the effectiveness of treatments; analyzing patient data and outcomes. Accurate percentage calculations are critical in healthcare for ensuring patient safety and treatment efficacy.
Beyond the Basics: More Complex Percentage Problems
While "5 is what percent of 50?" is a relatively simple problem, the principles involved can be applied to more complex scenarios. Consider these examples:
-
Finding the Whole: If 20% of a number is 10, what is the number? This requires rearranging the percentage formula to solve for the "whole."
-
Finding the Part: What is 35% of 200? This involves substituting the known values into the percentage formula to find the "part."
-
Percentage Increase/Decrease: A product's price increased from $50 to $60. What is the percentage increase? This requires calculating the difference, then expressing it as a percentage of the original price.
-
Compound Percentages: Calculating compound interest involves applying a percentage repeatedly over time.
Mastering Percentages: Tips and Tricks
-
Practice regularly: The more you practice, the more comfortable you will become with percentage calculations. Work through various problems, starting with simple ones and gradually increasing the difficulty.
-
Use different methods: Experiment with the various methods described above to find the approach that best suits your understanding and preference.
-
Visual aids: Using diagrams or charts can help visualize percentage problems and make them easier to understand.
-
Check your work: Always double-check your calculations to ensure accuracy. A simple mistake can lead to significant errors, especially in financial or scientific contexts.
-
Utilize online calculators and resources: While understanding the underlying principles is crucial, online calculators can be helpful for quick calculations or verifying your work. However, it is imperative to grasp the fundamental concepts before relying solely on such tools.
-
Understand the context: Always consider the context of the problem. Understanding what the percentage represents in the real world can help you interpret the results and make informed decisions.
Conclusion: The Importance of Percentage Proficiency
The ability to understand and calculate percentages is a fundamental skill with far-reaching applications. From everyday budgeting to complex financial analysis, a strong grasp of percentage concepts is essential for making informed decisions and effectively navigating numerous aspects of life. By mastering the methods and principles outlined in this article, you can build a solid foundation for tackling percentage problems of varying complexity and unlock the power of this crucial mathematical tool. The seemingly simple question, "5 is what percent of 50?", serves as a springboard to a much deeper understanding of a concept vital for success in various domains. Continue practicing, explore different problem types, and you'll find that your proficiency in percentages will grow exponentially.
Latest Posts
Latest Posts
-
Why Is The Product Of Saponification A Salt
Apr 16, 2025
-
What Is 15 Out Of 20 As A Percentage
Apr 16, 2025
-
Cuanto Es 90 Pulgadas En Centimetros
Apr 16, 2025
-
Cuantos Grados Centigrados Son 61 Fahrenheit
Apr 16, 2025
-
Can Travel Through A Empty Space
Apr 16, 2025
Related Post
Thank you for visiting our website which covers about 5 Is What Percent Of 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.