50 Out Of 80 As A Percentage
Kalali
Apr 18, 2025 · 5 min read
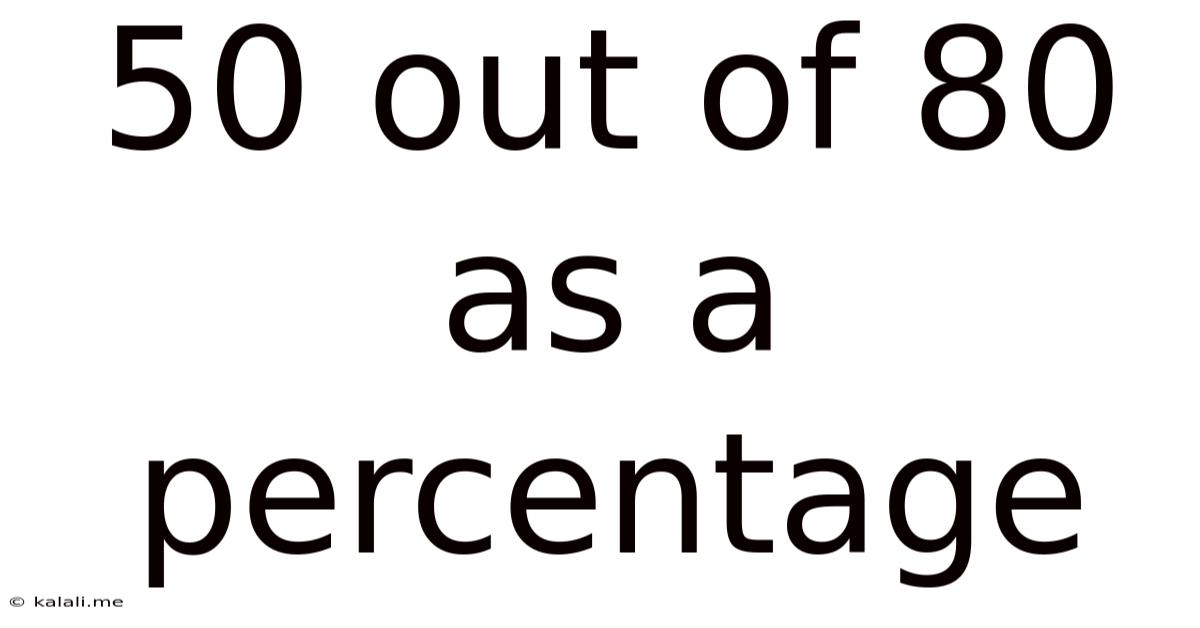
Table of Contents
Decoding the Percentage: 50 out of 80 as a Percentage and its Applications
Calculating percentages is a fundamental skill with widespread applications across various fields, from everyday budgeting to complex statistical analysis. Understanding how to express fractions as percentages is crucial for interpreting data and making informed decisions. This article delves into the specific calculation of 50 out of 80 as a percentage, providing a step-by-step explanation and exploring its practical uses in different contexts. We'll also touch upon related percentage calculations and how to avoid common mistakes. This comprehensive guide will equip you with the knowledge to confidently tackle similar percentage problems.
Meta Description: Learn how to calculate 50 out of 80 as a percentage. This comprehensive guide provides a step-by-step explanation, real-world examples, and explores the practical applications of percentage calculations. Master percentage conversions and avoid common errors.
Understanding Percentages: A Foundation
Before diving into the calculation of 50 out of 80, let's solidify our understanding of percentages. A percentage represents a fraction of 100. The word "percent" literally means "per hundred." Therefore, expressing a value as a percentage means expressing it as a fraction of 100. For instance, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Calculating 50 out of 80 as a Percentage: The Step-by-Step Guide
To calculate 50 out of 80 as a percentage, we follow these simple steps:
-
Express the values as a fraction: We represent "50 out of 80" as the fraction 50/80.
-
Convert the fraction to a decimal: Divide the numerator (50) by the denominator (80): 50 ÷ 80 = 0.625
-
Convert the decimal to a percentage: Multiply the decimal by 100: 0.625 × 100 = 62.5
-
Add the percentage symbol: Therefore, 50 out of 80 is equal to 62.5%.
Practical Applications of Percentage Calculations: Real-World Examples
The ability to calculate percentages is vital in numerous situations. Here are a few examples demonstrating the practical application of this skill, highlighting the relevance of understanding 62.5% as a result of 50 out of 80:
-
Academic Performance: Imagine a student scoring 50 marks out of a total of 80 marks in an exam. Their percentage score is 62.5%, providing a clear indication of their performance relative to the maximum possible score. This percentage can be compared to other students' scores or used to track academic progress. Understanding the percentage allows for a standardized comparison across different tests or assignments, even if the total marks vary.
-
Business and Finance: Businesses frequently use percentages to track sales, profits, and expenses. For example, if a company targets 80 sales and achieves 50, they can assess their performance as 62.5% of their target. This metric allows for effective monitoring and adjustment of sales strategies. Furthermore, calculating percentage changes in revenue, profit margins, and market share are crucial for financial planning and decision-making.
-
Sales and Discounts: Retail stores use percentages to advertise discounts. A "62.5% off" sale directly relates to a scenario where 50 items were sold out of an initial 80. This simplifies the understanding for customers and allows for easy comparison of different discounts offered by competing retailers.
-
Data Analysis and Statistics: In data analysis, percentages are used to present data in a concise and easily understandable manner. For instance, if a survey of 80 people shows 50 prefer a certain product, the result can be expressed as a 62.5% preference rate. This provides a clear visualization of the proportion of the population that favors the product. Furthermore, percentages are essential in calculating statistical measures such as mean, median, and mode.
-
Scientific Research: Percentage calculations are fundamental in scientific research for representing data and conducting statistical analysis. Experimental results often involve calculating the percentage of successful outcomes, or the percentage change in a measured variable. For example, in a biological experiment involving 80 subjects, where 50 showed a positive response, the success rate is 62.5%.
-
Everyday Life: From calculating tips at restaurants (e.g., 15% of the bill) to understanding interest rates on loans or savings accounts, percentages are an integral part of our daily lives. Even something as simple as determining the proportion of a recipe (e.g., using 62.5% of the required flour) uses percentage calculations.
Related Percentage Calculations and Avoiding Common Mistakes
Understanding the calculation of 50 out of 80 as a percentage also helps in tackling related problems:
-
Calculating the percentage of a given number: If you need to find 62.5% of another number, say 120, you simply multiply 120 by 0.625 (which is the decimal equivalent of 62.5%). This would give you 75.
-
Finding the original value: If you know a percentage (e.g., 62.5%) and the resulting value (e.g., 50), you can find the original value by setting up a proportion and solving for the unknown.
Common mistakes to avoid:
-
Incorrect fraction formation: Ensure the correct numerator and denominator are used in the fraction. "50 out of 80" should be written as 50/80, not 80/50.
-
Calculation errors: Double-check your calculations, especially when working with decimals. Use a calculator if necessary to minimize the risk of arithmetic errors.
-
Forgetting the percentage symbol: Always remember to include the "%" symbol to indicate that the result is a percentage.
-
Misinterpreting the context: Ensure you clearly understand the context of the problem. A poorly understood question can lead to a wrong calculation. For example, understanding the difference between percentage increase and percentage decrease.
Advanced Applications and Further Exploration
The principles of calculating percentages extend to more complex scenarios:
-
Compound interest: Compound interest calculations rely heavily on percentage calculations to determine the accumulated value of an investment over time.
-
Statistical significance: In statistical analysis, percentages help in determining the significance of results and interpreting probability.
-
Financial modeling: Percentage changes are crucial in forecasting and projecting financial performance.
Mastering percentage calculations is a valuable skill with far-reaching applications. Understanding how to calculate 50 out of 80 as a percentage, along with the related concepts and potential pitfalls, empowers you to analyze data, make informed decisions, and tackle various problems confidently, both in academic and professional settings. The ability to quickly and accurately convert fractions and decimals into percentages is a fundamental skill that strengthens your problem-solving capabilities in numerous contexts. Regular practice and attention to detail will solidify your understanding and ensure accuracy in your calculations.
Latest Posts
Latest Posts
-
What Percentage Is 12 Out Of 20
Apr 19, 2025
-
What Is The Least Common Multiple Of 40 16
Apr 19, 2025
-
How Many Hours Is 166 Minutes
Apr 19, 2025
-
What Is 20 Off Of 70
Apr 19, 2025
-
25 Is What Percent Of 65
Apr 19, 2025
Related Post
Thank you for visiting our website which covers about 50 Out Of 80 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.