What Percentage Is 12 Out Of 20
Kalali
Apr 19, 2025 · 5 min read
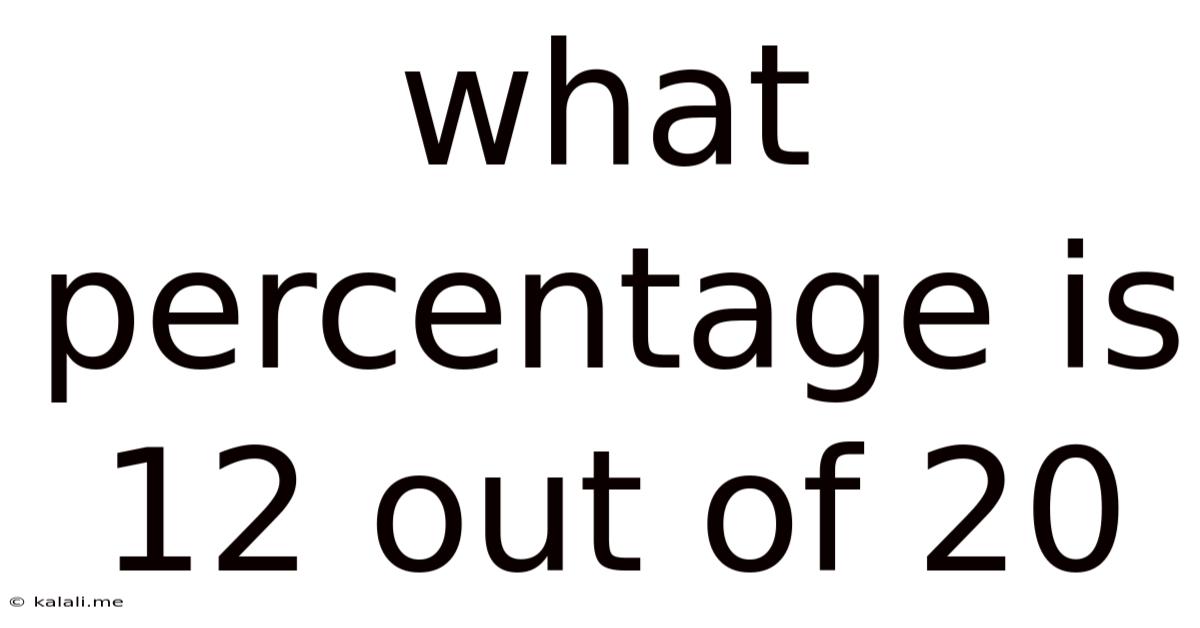
Table of Contents
What Percentage is 12 out of 20? A Deep Dive into Percentage Calculations and Applications
What percentage is 12 out of 20? The simple answer is 60%. But this seemingly straightforward question opens the door to a broader understanding of percentages, their calculation methods, and their widespread applications in various fields. This article will not only answer the initial question but also explore the underlying concepts, provide multiple calculation approaches, and demonstrate real-world examples of percentage usage.
Meta Description: Discover how to calculate percentages, understand the concept of "12 out of 20" as a percentage, and explore various applications of percentage calculations in everyday life and professional settings. Learn different calculation methods and explore related concepts.
Understanding Percentages: The Foundation
A percentage is a fraction or a ratio expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." Essentially, it's a way to express a proportion relative to a whole. For instance, 50% means 50 out of 100, which simplifies to 1/2 or 0.5.
Understanding percentages is crucial in numerous aspects of life. From calculating discounts and taxes to understanding statistical data and financial reports, percentages are a fundamental tool for interpreting and communicating numerical information.
Calculating "12 out of 20" as a Percentage: Three Methods
There are several ways to calculate what percentage 12 represents out of 20. Let's explore three common methods:
Method 1: The Fraction Method
This method involves expressing the given numbers as a fraction and then converting that fraction into a percentage.
- Form a fraction: Write 12 out of 20 as a fraction: 12/20
- Simplify the fraction (optional): Both 12 and 20 are divisible by 4. Simplifying the fraction gives us 3/5.
- Convert to a decimal: Divide the numerator (3) by the denominator (5): 3 ÷ 5 = 0.6
- Convert to a percentage: Multiply the decimal by 100: 0.6 x 100 = 60%
Therefore, 12 out of 20 is 60%.
Method 2: The Proportion Method
This method uses proportions to solve for the unknown percentage.
- Set up a proportion: We can set up a proportion like this: 12/20 = x/100, where 'x' represents the unknown percentage.
- Cross-multiply: Multiply 12 by 100 and 20 by x: 1200 = 20x
- Solve for x: Divide both sides by 20: x = 1200 ÷ 20 = 60
- Express as a percentage: x = 60%
Again, we find that 12 out of 20 is 60%.
Method 3: Using a Calculator
The simplest method is using a calculator. Simply divide 12 by 20 and then multiply the result by 100.
- Divide: 12 ÷ 20 = 0.6
- Multiply: 0.6 x 100 = 60%
Real-World Applications of Percentage Calculations
Percentages are ubiquitous in everyday life and professional settings. Here are some examples:
-
Retail and Sales: Discounts are often expressed as percentages. A "20% off" sale means you pay 80% of the original price. Calculating the final price after a discount requires understanding percentage reductions.
-
Finance and Investments: Interest rates on loans and savings accounts are expressed as percentages. Understanding compound interest, which involves calculating interest on both the principal and accumulated interest, relies heavily on percentage calculations. Return on investment (ROI) is also expressed as a percentage, indicating the profitability of an investment.
-
Taxes: Sales taxes, income taxes, and property taxes are all calculated as percentages of the taxable amount. Accurate tax calculations require a solid understanding of percentages.
-
Statistics and Data Analysis: Percentages are frequently used to represent proportions within datasets. For example, survey results are often presented as percentages to show the distribution of responses. Statistical measures like percentiles also rely on percentage calculations.
-
Science and Engineering: Percentages are used to express concentrations of solutions, efficiencies of machines, and error margins in measurements.
-
Everyday Life: Calculating tips in restaurants, determining the percentage of a task completed, or understanding nutritional information on food labels all involve percentage calculations.
Beyond the Basics: Advanced Percentage Concepts
While calculating a simple percentage like 12 out of 20 is straightforward, more complex scenarios exist:
-
Percentage Increase and Decrease: Calculating the percentage change between two values requires understanding the formula: [(New Value - Old Value) / Old Value] x 100%. For example, if a price increases from $10 to $12, the percentage increase is [(12 - 10) / 10] x 100% = 20%.
-
Percentage Points: This is often confused with percentages. A percentage point refers to an absolute difference between two percentages. For instance, if interest rates rise from 5% to 8%, this is a 3-percentage-point increase, not a 60% increase.
-
Compounding Percentages: This involves applying a percentage change repeatedly over time. Compound interest is a classic example where interest earned in one period is added to the principal, and the interest for the next period is calculated on the new, larger principal.
-
Weighted Averages: In situations where different data points have varying importance, weighted averages are used, where each data point contributes a percentage to the overall average.
Troubleshooting Common Percentage Calculation Errors
Several common mistakes can occur when calculating percentages:
-
Incorrect order of operations: Remember to follow the order of operations (PEMDAS/BODMAS) when performing calculations involving multiple steps.
-
Confusing percentage change with percentage points: Clearly distinguish between these two concepts.
-
Rounding errors: Rounding intermediate results can lead to inaccuracies in the final answer. It's best to retain more decimal places during intermediate calculations and round only the final result.
-
Incorrect formula application: Ensure you are using the correct formula for the specific percentage calculation you are performing.
Conclusion: Mastering Percentages for a Data-Driven World
The simple question "What percentage is 12 out of 20?" serves as a gateway to understanding the broader importance of percentages in various fields. From everyday transactions to complex financial analyses, mastering percentage calculations is essential for navigating a data-driven world. By understanding the different calculation methods, applying the correct formulas, and avoiding common errors, you can confidently utilize percentages to interpret information, make informed decisions, and communicate effectively. The ability to accurately and efficiently calculate percentages is a valuable skill applicable across numerous disciplines and contexts. Continue practicing and exploring different applications to further enhance your understanding and proficiency.
Latest Posts
Latest Posts
-
How Many Cm In 71 Inches
Apr 20, 2025
-
What Is 5 5 In Meters
Apr 20, 2025
-
What Is The Percent Of 1 6
Apr 20, 2025
-
What Percent Of 300 Is 50
Apr 20, 2025
-
How Many Cups Equal 15 Oz
Apr 20, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Is 12 Out Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.