51 Is What Percent Of 60
Kalali
Apr 18, 2025 · 5 min read
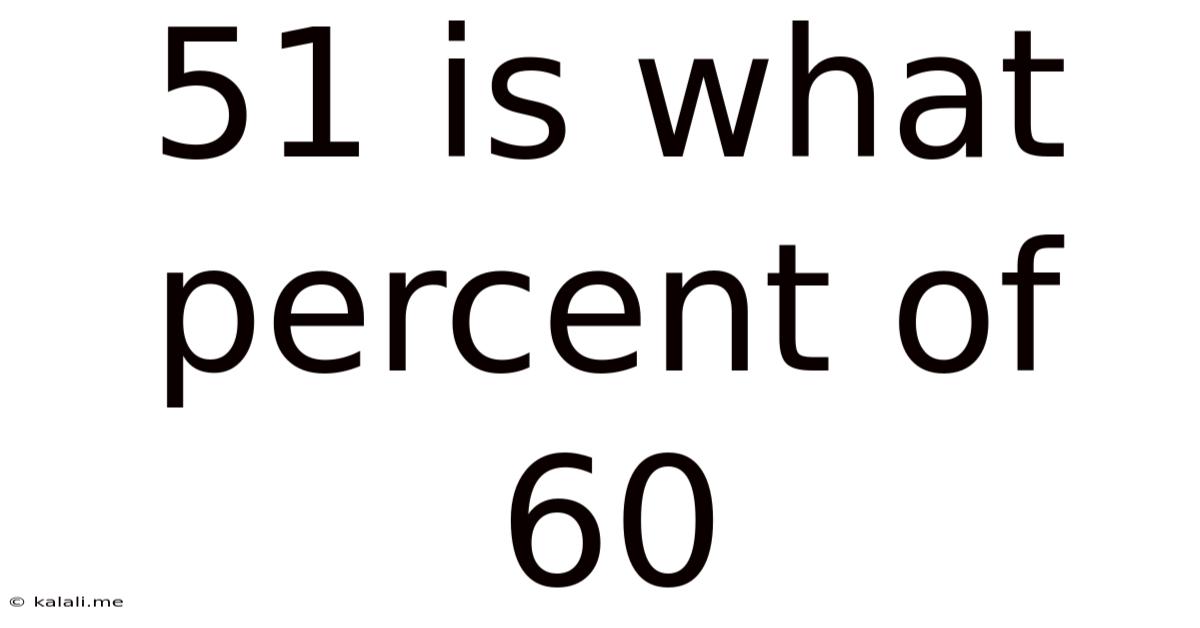
Table of Contents
51 is What Percent of 60? A Comprehensive Guide to Percentage Calculations
This seemingly simple question, "51 is what percent of 60?", opens the door to a world of percentage calculations crucial for various aspects of life, from everyday budgeting and shopping to complex financial analysis and scientific research. Understanding how to solve this type of problem is essential for navigating the numerical landscape of modern life. This comprehensive guide will not only provide the solution but also delve into the underlying concepts, alternative methods, and practical applications of percentage calculations. We'll explore various scenarios where this type of calculation is vital and provide you with the tools to confidently tackle similar problems.
Meta Description: Learn how to calculate percentages with ease! This detailed guide explains how to find what percent 51 is of 60, covering various methods and practical applications of percentage calculations in everyday life and beyond. Master percentage calculations today!
Understanding Percentages
Before diving into the calculation, let's establish a firm understanding of percentages. A percentage is a way of expressing a number as a fraction of 100. The symbol "%" signifies "per cent," meaning "out of one hundred." Therefore, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5.
Percentages are used extensively to represent proportions, ratios, and changes in various contexts. For instance, you might see percentage discounts in a store, interest rates on loans, or growth rates in the economy, all expressed as percentages.
Method 1: Using the Formula
The most straightforward method to determine what percent 51 is of 60 involves using the basic percentage formula:
(Part / Whole) x 100% = Percentage
In this case:
- Part: 51 (the number we're interested in expressing as a percentage)
- Whole: 60 (the total or the base number)
Substituting these values into the formula:
(51 / 60) x 100% = 0.85 x 100% = 85%
Therefore, 51 is 85% of 60.
Method 2: Setting up a Proportion
Another effective approach involves setting up a proportion. A proportion expresses the equality of two ratios. We can represent the problem as:
51/60 = x/100
Where 'x' represents the percentage we want to find. To solve for 'x,' we cross-multiply:
60x = 5100
Then, divide both sides by 60:
x = 5100 / 60 = 85
Therefore, x = 85%, confirming that 51 is 85% of 60.
Method 3: Using Decimal Equivalents
This method involves converting the fraction 51/60 into a decimal and then multiplying by 100% to obtain the percentage.
First, divide 51 by 60:
51 ÷ 60 = 0.85
Next, multiply the decimal by 100%:
0.85 x 100% = 85%
Again, this confirms that 51 is 85% of 60.
Practical Applications of Percentage Calculations
Understanding percentage calculations extends far beyond simple mathematical problems. Here are several real-world applications:
-
Retail Discounts: Calculating discounts is a common application. If an item is 20% off its original price of $60, you can calculate the discount as (20/100) x $60 = $12. The sale price would be $60 - $12 = $48.
-
Tax Calculations: Sales tax, income tax, and other taxes are often expressed as percentages. If the sales tax is 8%, you can calculate the tax on a $50 purchase as (8/100) x $50 = $4. The total cost would be $50 + $4 = $54.
-
Financial Investments: Interest rates on savings accounts, loans, and investments are usually presented as percentages. Understanding percentage calculations is essential to evaluate the returns or costs associated with these financial products. For example, calculating compound interest involves repeated percentage calculations.
-
Grade Calculations: In education, grades are often expressed as percentages. If a student scores 45 out of 60 on a test, their percentage score is (45/60) x 100% = 75%.
-
Data Analysis and Statistics: Percentages are frequently used in data analysis and statistics to represent proportions, trends, and changes. This is crucial in fields such as market research, public health, and scientific research. For example, calculating the percentage of respondents who prefer a particular product in a survey relies on percentage calculations.
-
Tip Calculations: Calculating a tip at a restaurant often involves determining a percentage of the total bill. For example, a 15% tip on a $75 bill would be (15/100) x $75 = $11.25.
-
Commission Calculations: Sales representatives often earn a commission based on a percentage of their sales. Understanding percentage calculations is crucial for calculating their earnings.
-
Budgeting and Expense Tracking: Percentages help in budgeting by allowing you to allocate funds based on percentages of your total income. For example, allocating 30% of your income to rent.
-
Scientific Research: Percentage calculations are used extensively in scientific research, from calculating experimental error to analyzing data trends.
-
Cooking and Baking: Recipes often involve scaling ingredients up or down based on percentages. If a recipe calls for 20% flour, you need to calculate that percentage based on the total weight of ingredients.
Advanced Percentage Problems & Solving Strategies
While the example "51 is what percent of 60?" is relatively straightforward, more complex percentage problems may require multiple steps or different approaches. Here are some examples and strategies to tackle them:
-
Finding the whole when given the part and percentage: If you know that 30% of a number is 15, you can set up the equation: 0.30x = 15. Solving for x gives you x = 50, meaning the whole number is 50.
-
Finding the percentage increase or decrease: This involves calculating the change between two values and expressing that change as a percentage of the original value. For example, if a value increases from 50 to 60, the percentage increase is ((60-50)/50) x 100% = 20%.
-
Compound percentage changes: When percentages are applied repeatedly, the calculations become more complex. For example, calculating the final value after a 10% increase followed by a 5% decrease requires careful attention to the order of operations.
-
Problems involving multiple percentages: Problems may involve multiple percentages, such as calculating the final price after applying a discount and then adding sales tax.
Conclusion: Mastering Percentage Calculations
The ability to calculate percentages efficiently and accurately is a valuable skill applicable in numerous situations. This guide demonstrates several methods for solving problems like "51 is what percent of 60?", highlighting the versatility and importance of understanding percentage calculations in everyday life and beyond. By mastering these techniques, you can navigate numerical challenges with confidence and make informed decisions in various aspects of your life, from personal finance to professional endeavors. Remember to practice regularly to reinforce your understanding and build your problem-solving skills. The more you practice, the easier and more intuitive percentage calculations will become.
Latest Posts
Latest Posts
-
What Percent Of 60 Is 10
Apr 19, 2025
-
How Many Oz Of Butter Is 1 Cup
Apr 19, 2025
-
78 Inches In Feet And Inches
Apr 19, 2025
-
Cuanto Es 13 Grados Fahrenheit En Centigrados
Apr 19, 2025
-
How Much Is 39 Degrees Celsius In Fahrenheit
Apr 19, 2025
Related Post
Thank you for visiting our website which covers about 51 Is What Percent Of 60 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.