What Percent Of 60 Is 10
Kalali
Apr 19, 2025 · 5 min read
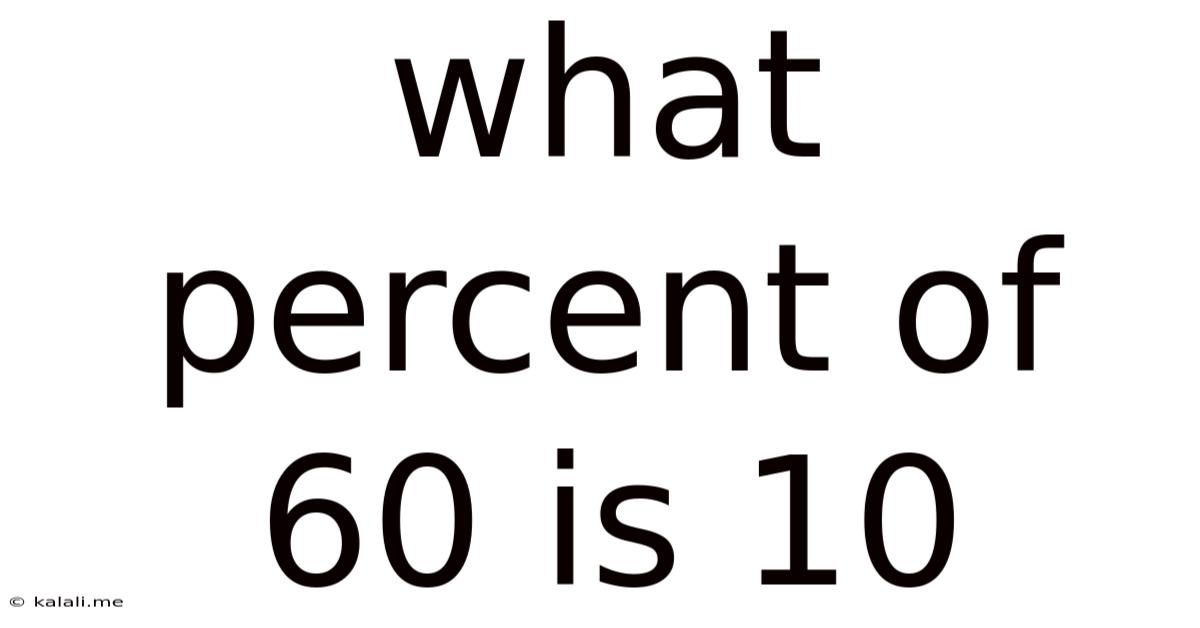
Table of Contents
What Percent of 60 is 10? A Deep Dive into Percentages and Their Applications
This seemingly simple question – "What percent of 60 is 10?" – opens the door to a broader understanding of percentages, their practical applications, and the mathematical principles behind them. This article will not only answer the question directly but also explore the various methods for calculating percentages, discuss their importance in diverse fields, and offer real-world examples to solidify your understanding.
Meta Description: Learn how to calculate percentages, understand what percentage of 60 is 10, and discover the numerous applications of percentages in everyday life and various professional fields. This comprehensive guide provides multiple approaches and real-world examples.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of a hundred." Therefore, 10% means 10 out of 100, which can be written as the fraction 10/100 or the decimal 0.1. Percentages are a common tool for representing proportions, ratios, and changes in value. They are used extensively in various fields, from finance and economics to statistics and everyday life.
Method 1: Using the Proportion Method to Find the Percentage
The most straightforward way to determine what percent of 60 is 10 is to use the proportion method. This method sets up a proportion, equating two ratios:
- Ratio 1: The part (10) to the whole (60)
- Ratio 2: The percentage (x) to 100
This translates into the following equation:
10/60 = x/100
To solve for x (the percentage), we cross-multiply:
10 * 100 = 60 * x
1000 = 60x
Now, we divide both sides by 60:
x = 1000/60
x = 16.666...%
Therefore, 10 is approximately 16.67% of 60. We can round to two decimal places for practical purposes.
Method 2: Using Decimal Conversion
This method involves converting the fraction representing the part to the whole into a decimal and then multiplying by 100 to express it as a percentage.
-
Form the fraction: 10/60
-
Simplify the fraction (optional but helpful): 10/60 simplifies to 1/6
-
Convert the fraction to a decimal: 1 ÷ 6 ≈ 0.1667
-
Multiply the decimal by 100 to get the percentage: 0.1667 * 100 ≈ 16.67%
This method offers a slightly different approach but arrives at the same answer.
Method 3: Using the Percentage Formula
The percentage formula provides a more generalized approach to solving percentage problems. The formula is:
(Part / Whole) * 100 = Percentage
In our case:
(10 / 60) * 100 = Percentage
(0.1667) * 100 ≈ 16.67%
This method clearly shows the direct relationship between the part, the whole, and the resulting percentage.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is essential in various aspects of life. Here are some examples:
- Finance: Calculating interest rates on loans and investments, determining discounts on purchases, understanding tax rates, analyzing profit margins, and evaluating return on investment (ROI). For instance, if you invest $1000 and receive a return of $100, your ROI is 10%.
- Sales and Marketing: Analyzing sales figures, calculating conversion rates (e.g., the percentage of website visitors who make a purchase), determining discount percentages, evaluating the effectiveness of marketing campaigns. If a store had 60 customers and 10 made a purchase, their conversion rate would be 16.67%.
- Statistics and Data Analysis: Representing data in the form of percentages, calculating percentages changes, creating charts and graphs using percentage data, conducting statistical analysis involving percentages.
- Education: Calculating grades based on scores, determining the percentage of students who passed an exam, analyzing performance metrics.
- Everyday Life: Calculating tips in restaurants, understanding sales tax, determining discounts, figuring out proportions in recipes. If a recipe calls for 60 grams of flour and you want to use only 10 grams, you are using approximately 16.67% of the original recipe.
Beyond the Basics: More Complex Percentage Problems
While the question "What percent of 60 is 10?" provides a foundation, understanding percentages involves tackling more complex problems. Consider these scenarios:
- Finding the whole when given a part and a percentage: If 20% of a number is 15, what is the number? This requires rearranging the percentage formula.
- Finding the part when given the whole and a percentage: What is 35% of 200? This is a direct application of the percentage formula.
- Calculating percentage change (increase or decrease): If a value increases from 50 to 60, what is the percentage increase? This involves calculating the difference, dividing by the original value, and multiplying by 100.
- Compound percentages: Calculating percentages on percentages, as often encountered in compound interest calculations.
Mastering these more complex scenarios requires a firm grasp of the fundamental principles discussed earlier.
Practical Tips for Accurate Percentage Calculations
- Use a calculator: For complex calculations, using a calculator ensures accuracy and saves time.
- Understand rounding: Rounding off percentages appropriately is crucial to avoid misleading interpretations. Typically, rounding to two decimal places is sufficient for most applications.
- Check your work: Always double-check your calculations to minimize errors. One way is to estimate the answer first, then compare it to your calculated result. If there's a large discrepancy, review your steps.
- Practice regularly: The best way to improve your proficiency in percentage calculations is through consistent practice. Work through various problems, starting with simpler examples and gradually progressing to more complex ones.
Conclusion: The Ubiquity of Percentages
The seemingly simple question of "What percent of 60 is 10?" serves as a gateway to understanding the power and versatility of percentages. This fundamental concept underpins numerous calculations across diverse fields, making it an indispensable tool in various aspects of life – from managing personal finances to analyzing complex datasets. By mastering the methods presented here and practicing regularly, you will equip yourself with a valuable skill applicable in numerous contexts. The ability to quickly and accurately calculate percentages is a key skill for anyone seeking to navigate the numerical world effectively. Remember to always check your work and utilize calculators when dealing with complex percentage problems to maintain accuracy. The understanding of percentages is not just a mathematical skill, it's a crucial life skill.
Latest Posts
Latest Posts
-
What Is The Reciprocal Of 6
Apr 22, 2025
-
At What Temperature Does Blood Boil
Apr 22, 2025
-
What Is 8 12 As A Percentage
Apr 22, 2025
-
2 Out Of 3 As A Percentage
Apr 22, 2025
-
How Many Liters In 64 Ounces
Apr 22, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 60 Is 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.