What Is 8/12 As A Percentage
Kalali
Apr 22, 2025 · 5 min read
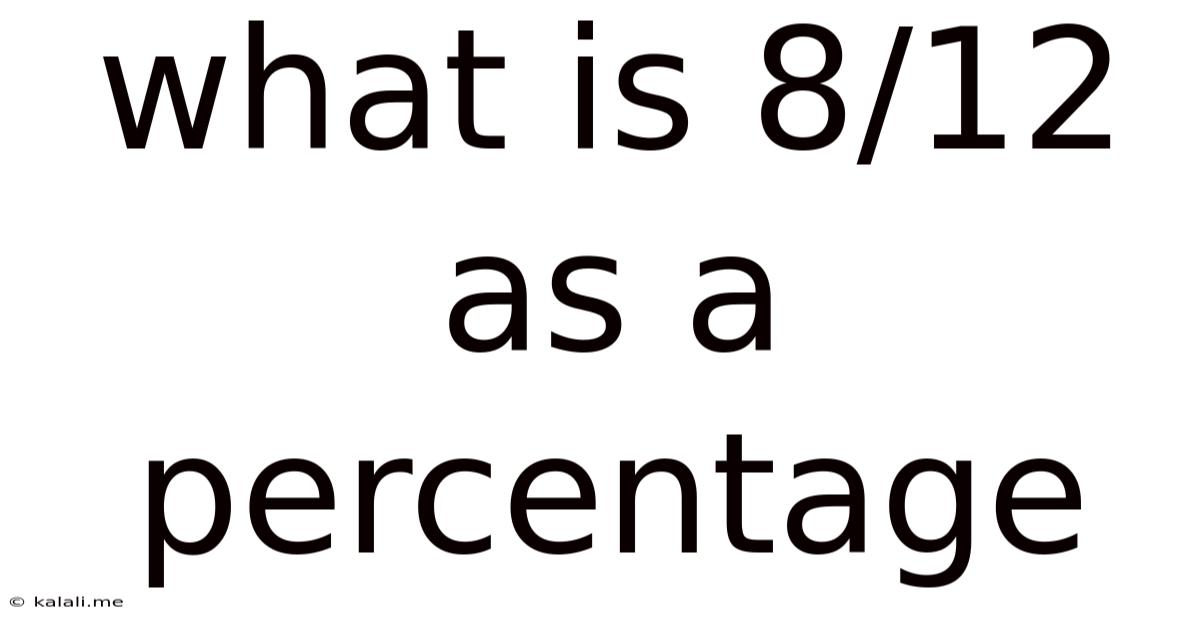
Table of Contents
What is 8/12 as a Percentage? A Comprehensive Guide to Fraction-to-Percentage Conversion
The question, "What is 8/12 as a percentage?" might seem simple at first glance. However, understanding how to convert fractions to percentages is a fundamental skill with wide-ranging applications in various fields, from everyday budgeting to advanced statistical analysis. This comprehensive guide will not only answer this specific question but also equip you with the knowledge to tackle similar conversions with confidence. We'll explore the core concepts, delve into different methods of calculation, and discuss practical applications of this essential mathematical skill.
Meta Description: Learn how to convert fractions to percentages with a detailed explanation of converting 8/12. This guide covers multiple calculation methods, practical applications, and related concepts for a comprehensive understanding.
Understanding Fractions and Percentages
Before diving into the conversion, let's briefly review the fundamental concepts of fractions and percentages.
-
Fractions: A fraction represents a part of a whole. It's composed of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates the number of parts you have, while the denominator indicates the total number of equal parts the whole is divided into. In our case, 8/12 means 8 parts out of a total of 12 equal parts.
-
Percentages: A percentage is a way of expressing a fraction or a decimal as a portion of 100. The symbol "%" represents "per hundred," indicating the proportion relative to a whole that is divided into 100 equal parts. For instance, 50% means 50 out of 100, or 50/100.
Method 1: Simplifying the Fraction Before Conversion
The most straightforward approach to converting 8/12 to a percentage involves simplifying the fraction first. Simplifying a fraction means reducing it to its lowest terms by dividing both the numerator and the denominator by their greatest common divisor (GCD).
-
Find the GCD: The greatest common divisor of 8 and 12 is 4.
-
Simplify the Fraction: Divide both the numerator and denominator by 4: 8 ÷ 4 = 2 12 ÷ 4 = 3 Therefore, 8/12 simplifies to 2/3.
-
Convert the Simplified Fraction to a Percentage: To convert a fraction to a percentage, divide the numerator by the denominator and then multiply the result by 100: 2 ÷ 3 ≈ 0.6667 0.6667 × 100 ≈ 66.67%
Therefore, 8/12 is equal to 66.67%. Note that we use the approximation symbol (≈) because the decimal 0.6667 is a recurring decimal, meaning the "6" repeats infinitely. For practical purposes, rounding to two decimal places is generally sufficient.
Method 2: Direct Conversion Without Simplification
You can also convert 8/12 to a percentage directly without simplifying the fraction first. This method involves the same core principle: dividing the numerator by the denominator and multiplying by 100.
-
Divide the Numerator by the Denominator: 8 ÷ 12 ≈ 0.6667
-
Multiply by 100 to Convert to Percentage: 0.6667 × 100 ≈ 66.67%
This method yields the same result as Method 1, demonstrating that simplifying the fraction beforehand is a matter of preference and can sometimes make the calculation easier, especially with larger numbers.
Method 3: Using Proportions
Another way to approach this problem is by using proportions. We can set up a proportion to find the equivalent percentage:
8/12 = x/100
To solve for x (the percentage), we can cross-multiply:
12x = 800
Now, divide both sides by 12:
x = 800/12 ≈ 66.67
Therefore, x ≈ 66.67%, confirming our previous results. This method emphasizes the relationship between the fraction and the percentage as equivalent ratios.
Practical Applications of Fraction-to-Percentage Conversion
The ability to convert fractions to percentages has numerous practical applications in various aspects of life:
-
Financial Calculations: Calculating discounts, interest rates, profit margins, and tax rates often requires converting fractions to percentages. For example, if a store offers a 1/4 discount, you need to convert this fraction (1/4 = 25%) to understand the actual discount amount.
-
Data Analysis and Statistics: Many statistical measures and data representations rely on percentages. For instance, expressing survey results, market share, or success rates often involves converting fractions representing proportions into percentages for easier interpretation and comparison.
-
Scientific Calculations and Measurements: In scientific experiments and measurements, converting fractions to percentages is crucial for expressing precision and accuracy. For instance, calculating experimental error or expressing the concentration of a solution frequently involves percentage representation.
-
Everyday Life: Understanding percentages helps in comprehending various situations, such as calculating tips in restaurants, understanding sales tax rates, or evaluating the nutritional content of food products based on percentage values listed on labels.
Further Exploration: Working with More Complex Fractions
While 8/12 is a relatively simple fraction, the same principles apply to more complex fractions. The key steps remain consistent:
-
Simplify the fraction (if possible). This reduces the numbers and simplifies the subsequent calculation.
-
Divide the numerator by the denominator. This gives you the decimal equivalent of the fraction.
-
Multiply the decimal by 100 to obtain the percentage. Remember to round off to an appropriate number of decimal places depending on the context and required precision.
Conclusion: Mastering Fraction-to-Percentage Conversions
Converting fractions to percentages is a fundamental mathematical skill with broad applicability. Understanding the underlying principles and mastering different calculation methods—simplifying the fraction, direct conversion, or using proportions—will empower you to tackle a wide range of percentage-related problems with confidence. This skill is not just essential for academic pursuits but also plays a significant role in navigating various aspects of everyday life and professional endeavors. By practicing these techniques, you'll enhance your numerical literacy and improve your ability to analyze and interpret data presented in fractional or percentage formats. Remember to always check your work and consider the context to determine the appropriate level of precision when rounding your final answer.
Latest Posts
Latest Posts
-
What Has A Definite Shape And Volume
Apr 22, 2025
-
How Many Grams In A 8th Of An Ounce
Apr 22, 2025
-
What Is Two Thirds Of 100
Apr 22, 2025
-
What Is 6 25 As A Fraction
Apr 22, 2025
-
44 Out Of 60 As A Percentage
Apr 22, 2025
Related Post
Thank you for visiting our website which covers about What Is 8/12 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.