6 4 As A Mixed Number
Kalali
Apr 13, 2025 · 5 min read
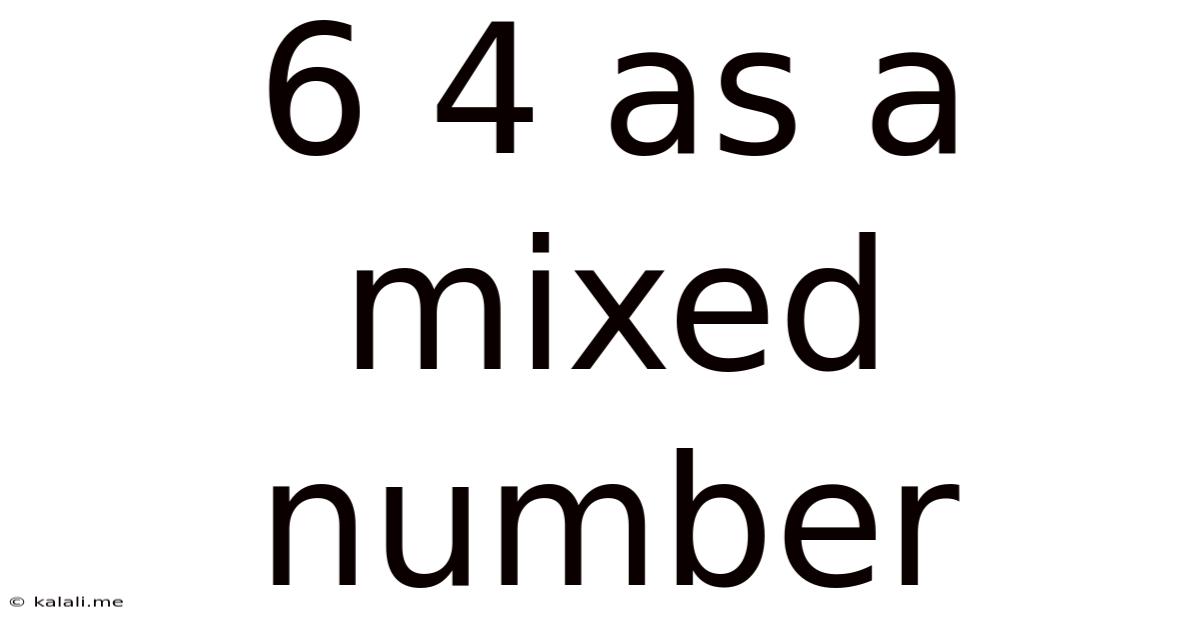
Table of Contents
Understanding 6 4/4 as a Mixed Number and its Implications
This article delves deep into the concept of 6 4/4 as a mixed number, explaining its representation, simplification, and its broader implications within the world of fractions and mathematics. We'll explore why this specific example is crucial for understanding the relationship between improper fractions and mixed numbers, and how to effectively convert between the two. Understanding this foundational concept is vital for success in more advanced mathematical concepts.
Meta Description: Learn how to understand and simplify the mixed number 6 4/4. This comprehensive guide explores the conversion between improper fractions and mixed numbers, clarifying common misconceptions and providing practical examples.
What is a Mixed Number?
A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator (the top number) is smaller than the denominator (the bottom number). For example, 2 ½, 3 ⅔, and 1 ¼ are all mixed numbers. They represent a quantity that's more than a whole number but less than the next whole number.
What is an Improper Fraction?
An improper fraction is a fraction where the numerator is greater than or equal to the denominator. For instance, 5/4, 7/3, and 8/8 are all improper fractions. These fractions represent a quantity equal to or greater than one whole.
The Significance of 6 4/4
The mixed number 6 4/4 presents a unique opportunity to understand the fundamental relationship between improper fractions and mixed numbers. At first glance, it might seem straightforward, but it highlights a crucial aspect of fraction simplification: the ability to represent the same quantity in different ways.
Let's break it down:
-
The Whole Number Component: The '6' in 6 4/4 represents six complete wholes.
-
The Fractional Component: The '4/4' represents one whole (as the numerator and denominator are equal).
Therefore, 6 4/4 is equivalent to six wholes plus one whole, totaling seven wholes.
Converting Improper Fractions to Mixed Numbers: A Step-by-Step Guide
The process of converting an improper fraction to a mixed number involves division. Let's use the example of 11/3:
-
Divide the numerator by the denominator: 11 ÷ 3 = 3 with a remainder of 2.
-
The quotient becomes the whole number: The 3 is our whole number.
-
The remainder becomes the numerator of the fraction: The 2 becomes the numerator.
-
The denominator remains the same: The 3 remains the denominator.
Therefore, 11/3 converts to the mixed number 3 ⅔.
Converting Mixed Numbers to Improper Fractions: A Step-by-Step Guide
Converting a mixed number to an improper fraction involves the reverse process. Let's use the mixed number 2 ¾ as an example:
-
Multiply the whole number by the denominator: 2 x 4 = 8
-
Add the result to the numerator: 8 + 3 = 11
-
The result becomes the new numerator: 11 is our new numerator.
-
The denominator remains the same: The denominator remains 4.
Therefore, 2 ¾ converts to the improper fraction 11/4.
Why is Understanding 6 4/4 Important?
The seemingly simple example of 6 4/4 serves as a cornerstone for understanding several key mathematical concepts:
-
Simplifying Fractions: 6 4/4 simplifies to 7. This demonstrates the importance of simplifying fractions to their lowest terms for clarity and ease of calculation. Failing to simplify can lead to unnecessary complexity in more advanced problems.
-
Equivalence of Fractions: 6 4/4 is equivalent to 7/1, highlighting the concept that multiple fractions can represent the same value. This understanding is crucial for comparing and manipulating fractions effectively.
-
Foundation for Algebra: The process of converting between improper fractions and mixed numbers lays a strong foundation for understanding algebraic manipulations involving fractions. These skills are essential for solving more complex equations and inequalities.
-
Real-World Applications: Understanding fractions is crucial in everyday life – from cooking and baking to measuring materials for home improvement projects. The ability to convert between improper fractions and mixed numbers makes these tasks much simpler and more accurate.
Common Mistakes and How to Avoid Them
Many students encounter common pitfalls when working with improper fractions and mixed numbers. Here are some common errors and how to avoid them:
-
Incorrectly Converting Improper Fractions: A common mistake is misinterpreting the remainder during the division process. Always double-check your division to ensure accuracy.
-
Forgetting to Simplify: After converting to a mixed number, always check if the fractional component can be simplified. For example, 6 2/4 should be simplified to 6 ½.
-
Incorrect Conversion to Improper Fractions: Errors can occur when multiplying the whole number and denominator or when adding the result to the numerator. Careful attention to each step is essential.
Advanced Applications and Extensions
The principles learned through understanding 6 4/4 extend to more complex mathematical concepts:
-
Working with Negative Fractions: The same conversion methods apply to negative improper fractions and mixed numbers. Remember to maintain the negative sign throughout the process.
-
Adding and Subtracting Mixed Numbers: The ability to convert between improper fractions and mixed numbers is crucial for efficiently adding and subtracting mixed numbers. Often, converting to improper fractions first simplifies the addition or subtraction process.
-
Multiplying and Dividing Mixed Numbers: While it's possible to multiply and divide mixed numbers directly, converting them to improper fractions usually simplifies the calculation significantly, leading to more accurate results.
-
Solving Equations with Fractions: The ability to manipulate and convert between improper fractions and mixed numbers is essential when working with equations involving fractions.
Conclusion: Mastering the Fundamentals
6 4/4, though seemingly simple, acts as a powerful gateway to understanding the intricacies of fractions. Mastering the conversion between improper fractions and mixed numbers is essential for success in various mathematical contexts. By understanding the underlying principles and avoiding common mistakes, students can build a strong foundation for more advanced mathematical concepts and confidently apply these skills in various real-world situations. Regular practice and a focus on accuracy will significantly improve proficiency in working with fractions. The ability to easily convert between improper fractions and mixed numbers will undoubtedly enhance your mathematical problem-solving skills.
Latest Posts
Latest Posts
-
What Percent Of 20 Is 12
Apr 14, 2025
-
The Set Of All Points In A Plane
Apr 14, 2025
-
8 Is What Percent Of 24
Apr 14, 2025
-
What Is 25 In A Fraction
Apr 14, 2025
-
What Is The Speed Of Sound In Fps
Apr 14, 2025
Related Post
Thank you for visiting our website which covers about 6 4 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.