60 Is What Percent Of 40
Kalali
Apr 26, 2025 · 5 min read
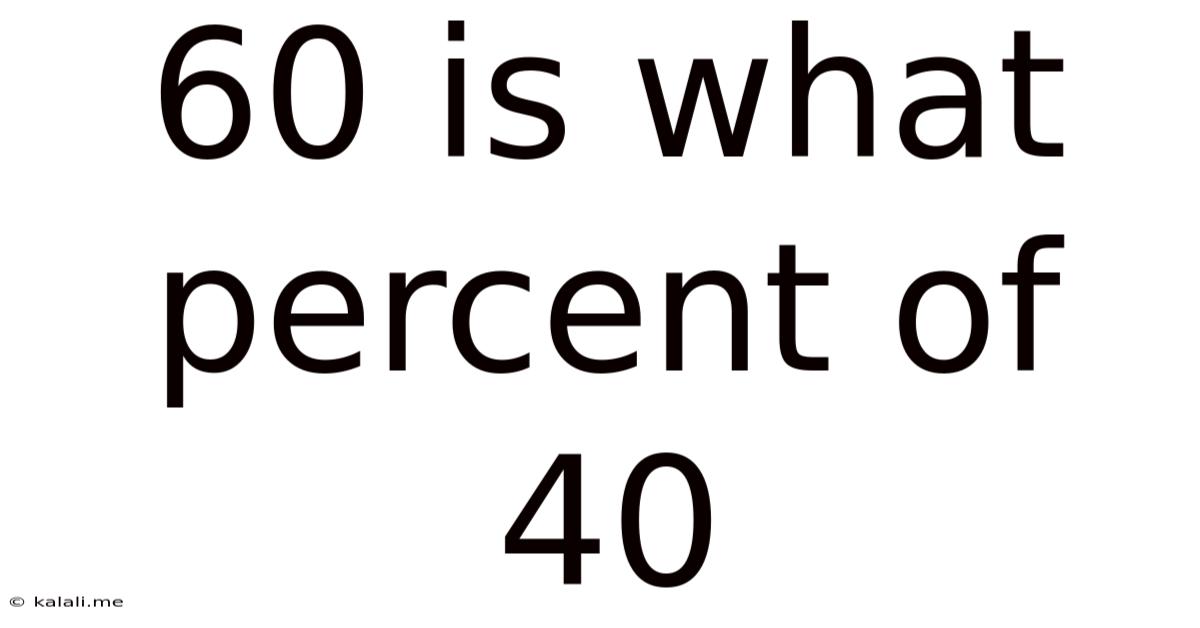
Table of Contents
60 is What Percent of 40? Understanding Percentages and Their Applications
This seemingly simple question, "60 is what percent of 40?", opens the door to a vast world of mathematical concepts and practical applications. Understanding percentages is crucial in various aspects of life, from calculating discounts and taxes to analyzing financial data and understanding statistical information. This article will not only answer the question directly but also delve into the underlying principles, providing a comprehensive understanding of percentages and their uses. We'll explore different methods for calculating percentages, address common misconceptions, and showcase real-world examples to solidify your grasp of this fundamental mathematical concept.
Meta Description: Learn how to calculate percentages with a detailed explanation of how to solve "60 is what percent of 40?". Discover diverse applications of percentage calculations in everyday life and beyond.
What is a Percentage?
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "per hundred" (from the Latin per centum). Percentages are represented by the symbol "%". For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5. Percentages are used to express proportions, ratios, and rates in a standardized and easily understandable format.
Calculating Percentages: The Fundamental Formula
The basic formula for calculating percentages is:
(Part / Whole) x 100% = Percentage
Where:
- Part: Represents the specific amount you're interested in.
- Whole: Represents the total amount.
- Percentage: The resulting percentage value.
Let's apply this formula to our original question: "60 is what percent of 40?"
In this case:
- Part = 60
- Whole = 40
Plugging these values into the formula:
(60 / 40) x 100% = 150%
Therefore, 60 is 150% of 40.
Understanding the Result: Percentages Greater Than 100%
The result of 150% might seem counterintuitive at first. We're used to percentages typically falling between 0% and 100%. However, percentages greater than 100% simply indicate that the "part" is larger than the "whole." This often happens when comparing values over time, growth rates, or when dealing with situations where an increase exceeds the original value.
Alternative Methods for Calculating Percentages
While the basic formula is straightforward, other methods can simplify the calculation, especially for mental arithmetic or when working with more complex scenarios.
-
Using Decimals: Convert the percentage to a decimal by dividing by 100. For example, 50% becomes 0.5. Then, multiply the decimal by the whole number. This method is particularly useful for calculations involving calculators or spreadsheets.
-
Proportions: Set up a proportion to solve for the unknown percentage. For instance, to find what percent 60 is of 40, we can set up the proportion:
x/100 = 60/40
Cross-multiplying and solving for x gives us x = 150.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is a valuable skill applicable across numerous fields:
-
Finance: Calculating interest rates, loan repayments, profits, losses, tax percentages, and investment returns.
-
Retail: Determining discounts, sales tax, markups, and profit margins. Understanding percentage discounts is crucial for consumers making informed purchasing decisions. For example, a 20% discount on a $100 item means a saving of $20, resulting in a final price of $80.
-
Science and Statistics: Expressing experimental results, analyzing data sets, and calculating probabilities. Percentages are widely used to represent statistical data clearly and concisely, making complex information readily accessible.
-
Everyday Life: Calculating tips in restaurants, figuring out the percentage of ingredients in a recipe, understanding nutritional labels, comparing prices, and comprehending survey results.
Common Mistakes to Avoid When Calculating Percentages
-
Confusing Part and Whole: Always correctly identify the "part" and the "whole" to avoid errors in the calculation.
-
Incorrect Decimal Conversion: Ensure accurate conversion of percentages to decimals when using this method.
-
Rounding Errors: Be mindful of rounding errors, especially when dealing with multiple percentage calculations. Rounding too early in the calculation can lead to significant inaccuracies in the final result.
Advanced Percentage Calculations
Beyond the basic formula, there are more complex percentage calculations to consider:
-
Percentage Change: Calculates the change between two values as a percentage. This is useful for tracking growth or decline in various aspects like population, sales, or investments. The formula is:
[(New Value - Old Value) / Old Value] x 100%
-
Percentage Point Difference: Represents the absolute difference between two percentages, not the relative change. For example, a change from 20% to 30% is a 10 percentage point increase, not a 50% increase.
-
Compound Interest: Interest calculated on both the principal amount and accumulated interest. This type of calculation is fundamental in understanding investment growth over time.
Practical Exercises
To reinforce your understanding, try solving these problems:
- What is 25% of 80?
- If a shirt costs $50 and is discounted by 15%, what is the final price?
- A store's sales increased from 1000 units to 1200 units. What is the percentage increase in sales?
- If a student scored 45 out of 60 on a test, what is their percentage score?
By working through these exercises, you’ll solidify your understanding of percentage calculations and their real-world applications. Remember that consistent practice is key to mastering this essential mathematical skill.
Conclusion
The question, "60 is what percent of 40?" serves as a springboard to understanding the broader concept of percentages. Percentages are a powerful tool used to express proportions, analyze data, and make informed decisions in various contexts. Mastering percentage calculations empowers you to navigate the quantitative aspects of everyday life, professional endeavors, and academic pursuits with confidence and accuracy. From simple discounts to complex financial analyses, the ability to confidently work with percentages is an invaluable skill. Remember the basic formula, practice regularly, and watch your understanding grow!
Latest Posts
Latest Posts
-
What Are The Characteristics Of Metals
Apr 27, 2025
-
Cuantos Son 10 Metros En Pies
Apr 27, 2025
-
What Is The Least Common Multiple Of 3 2
Apr 27, 2025
-
What Is The Input Of Photosynthesis
Apr 27, 2025
-
8 Is What Percent Of 60
Apr 27, 2025
Related Post
Thank you for visiting our website which covers about 60 Is What Percent Of 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.