60 Of 75 Is What Percent
Kalali
Apr 07, 2025 · 5 min read
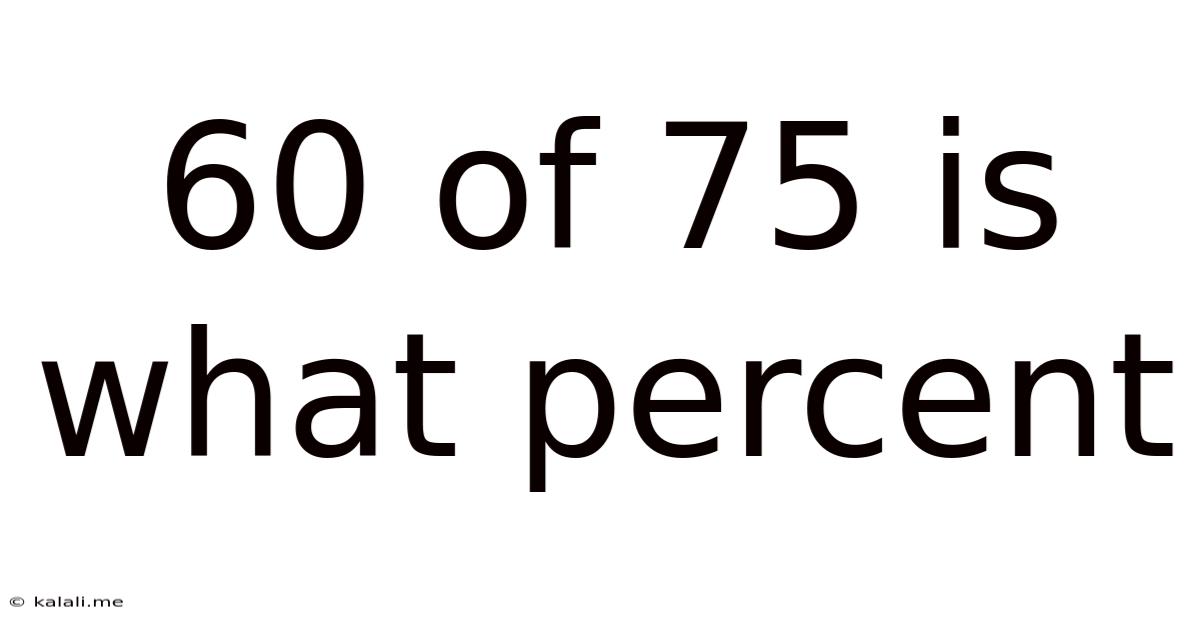
Table of Contents
- 60 Of 75 Is What Percent
- Table of Contents
- 60 out of 75 is What Percent? A Comprehensive Guide to Percentage Calculations
- Understanding Percentages
- Method 1: Using the Formula
- Method 2: Simplifying the Fraction
- Method 3: Using a Calculator
- Real-World Applications
- 1. Academic Performance:
- 2. Business and Finance:
- 3. Sales and Discounts:
- 4. Data Analysis and Statistics:
- 5. Everyday Budgeting:
- Beyond the Basics: Working with Different Percentages
- Advanced Percentage Calculations: Compound Interest
- Troubleshooting Common Percentage Calculation Mistakes
- Conclusion
- Latest Posts
- Latest Posts
- Related Post
60 out of 75 is What Percent? A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill with wide-ranging applications in various aspects of life, from everyday budgeting and shopping to complex scientific calculations and business analysis. Understanding how to determine percentages is crucial for making informed decisions and interpreting data effectively. This comprehensive guide will delve into the process of calculating percentages, specifically addressing the question: "60 out of 75 is what percent?" We'll explore different methods, provide detailed explanations, and examine real-world applications to solidify your understanding.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" comes from the Latin "per centum," meaning "out of a hundred." Therefore, a percentage represents a proportion or ratio out of a total of 100 parts. For example, 50% means 50 out of 100, or half.
Method 1: Using the Formula
The most straightforward method for calculating percentages involves a simple formula:
(Part / Whole) x 100% = Percentage
In our example, "60 out of 75," we have:
- Part: 60
- Whole: 75
Substituting these values into the formula, we get:
(60 / 75) x 100% = 80%
Therefore, 60 out of 75 is 80%.
Method 2: Simplifying the Fraction
Before applying the formula, you can simplify the fraction to make the calculation easier. The fraction 60/75 can be simplified by dividing both the numerator and the denominator by their greatest common divisor (GCD), which is 15:
60 ÷ 15 = 4 75 ÷ 15 = 5
This simplifies the fraction to 4/5. Now, we can apply the percentage formula:
(4 / 5) x 100% = 80%
This method demonstrates that simplifying the fraction first can often make the calculation less complex, especially when dealing with larger numbers.
Method 3: Using a Calculator
Most calculators have a percentage function that simplifies the process. You can input the fraction directly: 60 ÷ 75, and then multiply the result by 100. This method is particularly useful for complex calculations or when dealing with decimal numbers.
Real-World Applications
Understanding percentage calculations is vital in a wide array of real-world scenarios:
1. Academic Performance:
Imagine a student scored 60 out of 75 marks on a test. Using the methods described above, we've determined this represents 80%. This percentage helps the student understand their performance relative to the total marks available and allows teachers to assess the student's overall understanding of the subject matter.
2. Business and Finance:
Businesses frequently use percentages for various analyses such as calculating profit margins, growth rates, and discounts. For example, if a company made a profit of $60 million on a revenue of $75 million, their profit margin is 80%. Understanding these percentages is critical for making informed business decisions.
3. Sales and Discounts:
Retail stores often advertise discounts as percentages. If an item originally priced at $75 is discounted by 20%, the discount amount is (20/100) x $75 = $15. The final price after the discount is $75 - $15 = $60. Understanding percentage discounts helps consumers make informed purchasing decisions.
4. Data Analysis and Statistics:
Percentages are extensively used in data analysis and statistics to represent proportions and trends within datasets. For instance, if 60 out of 75 respondents in a survey answered "yes" to a particular question, the percentage of "yes" responses is 80%. This information is crucial for interpreting survey results and drawing meaningful conclusions.
5. Everyday Budgeting:
Percentages are instrumental in budgeting and financial planning. For example, if you aim to save 20% of your monthly income, and your income is $3000, your savings goal would be (20/100) x $3000 = $600.
Beyond the Basics: Working with Different Percentages
Let's explore scenarios where we need to find the percentage of a given number or work backward from a percentage to find the original value:
Example 1: Finding a Percentage of a Number:
What is 25% of 120?
The formula is: (Percentage/100) x Number
(25/100) x 120 = 30
Therefore, 25% of 120 is 30.
Example 2: Finding the Original Number from a Percentage:
If 80% of a number is 60, what is the number?
Let the number be 'x'. We can set up an equation:
0.8x = 60
Solving for 'x':
x = 60 / 0.8 = 75
Therefore, the original number is 75.
Advanced Percentage Calculations: Compound Interest
Compound interest is a powerful concept in finance that involves earning interest on both the principal amount and accumulated interest. It's a prime example of how percentages build upon each other over time. Calculating compound interest requires a slightly more advanced formula:
A = P (1 + r/n)^(nt)
Where:
- A = the future value of the investment/loan, including interest
- P = the principal investment amount (the initial deposit or loan amount)
- r = the annual interest rate (decimal)
- n = the number of times that interest is compounded per year
- t = the number of years the money is invested or borrowed for
Understanding compound interest allows you to make informed decisions about investments, loans, and long-term financial planning.
Troubleshooting Common Percentage Calculation Mistakes
While percentage calculations are relatively straightforward, several common mistakes can occur:
- Incorrect Order of Operations: Always follow the order of operations (PEMDAS/BODMAS) to ensure accurate calculations.
- Decimal Point Errors: Be mindful of decimal points when converting between fractions, decimals, and percentages. A misplaced decimal point can lead to significant errors.
- Misunderstanding the Formula: Make sure you understand the correct formula to use depending on the context of the problem.
- Rounding Errors: While rounding is sometimes necessary, be aware that it can introduce small inaccuracies, especially in complex calculations. Try to avoid rounding until the final step if possible.
Conclusion
Mastering percentage calculations is a valuable skill that extends far beyond the classroom. From analyzing data and making financial decisions to understanding discounts and interpreting statistical information, the ability to calculate and interpret percentages is essential for navigating many aspects of daily life. By understanding the fundamental formula, practicing various methods, and being aware of potential pitfalls, you can confidently tackle any percentage-related challenge and leverage this knowledge to make informed and effective decisions. The example of "60 out of 75 is what percent?" demonstrates a foundational percentage calculation, but the principles explained here can be applied to a vast array of more complex scenarios. Remember to practice consistently to reinforce your understanding and build your confidence in tackling more advanced percentage problems.
Latest Posts
Latest Posts
-
How Many Cups Are In 3 4 Of A Gallon
Apr 14, 2025
-
How To Find Lower Class Limits
Apr 14, 2025
-
How Tall Is 34 Inches In Feet
Apr 14, 2025
-
20 12 As A Mixed Number
Apr 14, 2025
-
Lowest Common Multiple Of 12 And 7
Apr 14, 2025
Related Post
Thank you for visiting our website which covers about 60 Of 75 Is What Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.