60 Out Of 240 As A Percentage
Kalali
Apr 08, 2025 · 4 min read
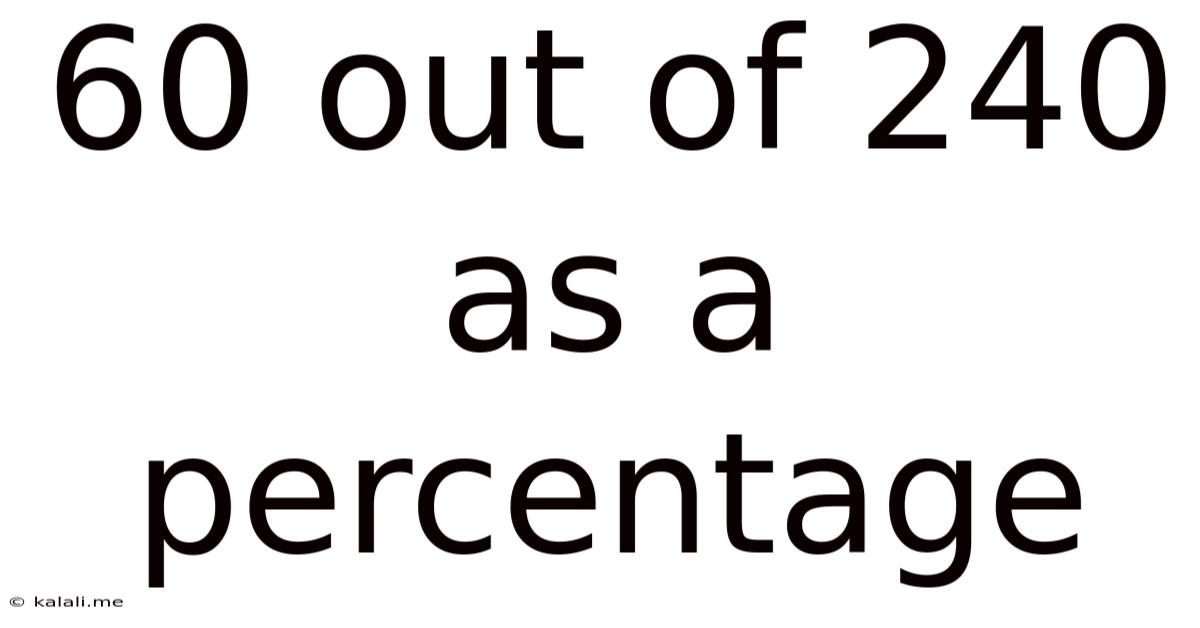
Table of Contents
60 Out of 240 as a Percentage: A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill applicable across numerous fields, from everyday budgeting to complex financial analysis. Understanding how to express a portion of a whole as a percentage is crucial for interpreting data, making informed decisions, and communicating effectively. This article provides a detailed explanation of how to calculate 60 out of 240 as a percentage, along with various methods, real-world applications, and troubleshooting common calculation errors. We'll also explore related percentage problems and delve into the broader context of percentage calculations.
Understanding Percentages: The Foundation
A percentage represents a fraction of 100. It's a way of expressing a proportion or ratio as a number out of 100. The symbol "%" signifies "per hundred." Therefore, 25% means 25 out of 100, or 25/100, which simplifies to 1/4. Understanding this basic concept is key to mastering percentage calculations.
Method 1: Using the Formula
The most straightforward way to calculate 60 out of 240 as a percentage is to use the basic percentage formula:
(Part / Whole) x 100% = Percentage
In this case:
- Part: 60 (the number representing the portion of the whole)
- Whole: 240 (the total number)
Plugging these values into the formula:
(60 / 240) x 100% = 25%
Therefore, 60 out of 240 is 25%.
Method 2: Simplifying the Fraction
Before applying the formula, you can simplify the fraction 60/240. Both the numerator (60) and the denominator (240) are divisible by 60:
60 ÷ 60 = 1 240 ÷ 60 = 4
This simplifies the fraction to 1/4. Converting this fraction to a percentage:
(1 / 4) x 100% = 25%
This method highlights the equivalence between fractions and percentages, demonstrating that simplifying the fraction can often make the percentage calculation easier.
Method 3: Using a Calculator
Calculators offer a quick and efficient way to compute percentages. Simply divide 60 by 240 and then multiply the result by 100:
60 ÷ 240 = 0.25 0.25 x 100 = 25%
Real-World Applications: Where Percentages Matter
Understanding percentage calculations is crucial in various everyday scenarios:
-
Finance: Calculating interest rates, discounts, tax percentages, profit margins, and investment returns. For example, if you invest $1000 and earn a 5% return, you've made $50.
-
Grades and Scores: Determining academic performance based on the percentage of correct answers on a test. If you answered 15 out of 20 questions correctly, your score is 75%.
-
Statistics: Analyzing data sets, interpreting survey results, and understanding statistical significance. For example, calculating the percentage of respondents who preferred a particular product.
-
Sales and Marketing: Tracking conversion rates, measuring the success of advertising campaigns, and calculating sales growth percentages. A 10% increase in sales is a significant achievement.
-
Shopping: Calculating discounts offered on sale items. A 20% discount on a $50 item means a savings of $10.
-
Cooking and Baking: Adjusting recipes based on percentages. If a recipe calls for 10% less sugar, you’ll need to adjust accordingly.
Common Mistakes to Avoid
Several common errors can occur when calculating percentages:
-
Incorrect Order of Operations: Remember to perform the division (Part/Whole) before multiplying by 100%.
-
Misinterpreting the Question: Carefully identify the "part" and the "whole" in the problem.
-
Rounding Errors: Be mindful of rounding errors, particularly when dealing with decimals. Consider maintaining several decimal places during calculations before rounding to the final answer.
Extending the Concept: Related Percentage Problems
Once you understand the fundamental concept of calculating percentages, you can tackle more complex scenarios:
-
Finding the Part: If you know the whole (240) and the percentage (25%), you can find the part: (25/100) * 240 = 60
-
Finding the Whole: If you know the part (60) and the percentage (25%), you can find the whole: 60 / (25/100) = 240
-
Percentage Increase/Decrease: Calculating percentage changes is essential for tracking growth or decline. For example, if sales increased from 100 to 120, the percentage increase is ((120-100)/100) x 100% = 20%.
-
Compound Percentage: Calculating percentage changes over multiple periods, considering the effect of compounding.
Conclusion: Mastering Percentage Calculations
Calculating 60 out of 240 as a percentage (25%) is a simple yet illustrative example of a fundamental mathematical concept with widespread applications. By understanding the basic formula, employing different calculation methods, and avoiding common pitfalls, you can confidently tackle a broad range of percentage problems in your personal and professional life. The ability to accurately and efficiently calculate percentages is a valuable skill that enhances your analytical and problem-solving capabilities. Remember to practice regularly and apply these techniques to real-world scenarios to reinforce your understanding and build confidence in your abilities. The more you practice, the more proficient you'll become in mastering the world of percentages.
Latest Posts
Latest Posts
-
What Is A 25 Out Of 40
Apr 17, 2025
-
Cuanto Es 91 Grados Fahrenheit En Centigrados
Apr 17, 2025
-
What Is 375 Celsius In Fahrenheit
Apr 17, 2025
-
10 To The Power Of 15
Apr 17, 2025
-
What Is 4 Percent Of 10000
Apr 17, 2025
Related Post
Thank you for visiting our website which covers about 60 Out Of 240 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.