64 Is What Percent Of 80
Kalali
Apr 12, 2025 · 5 min read
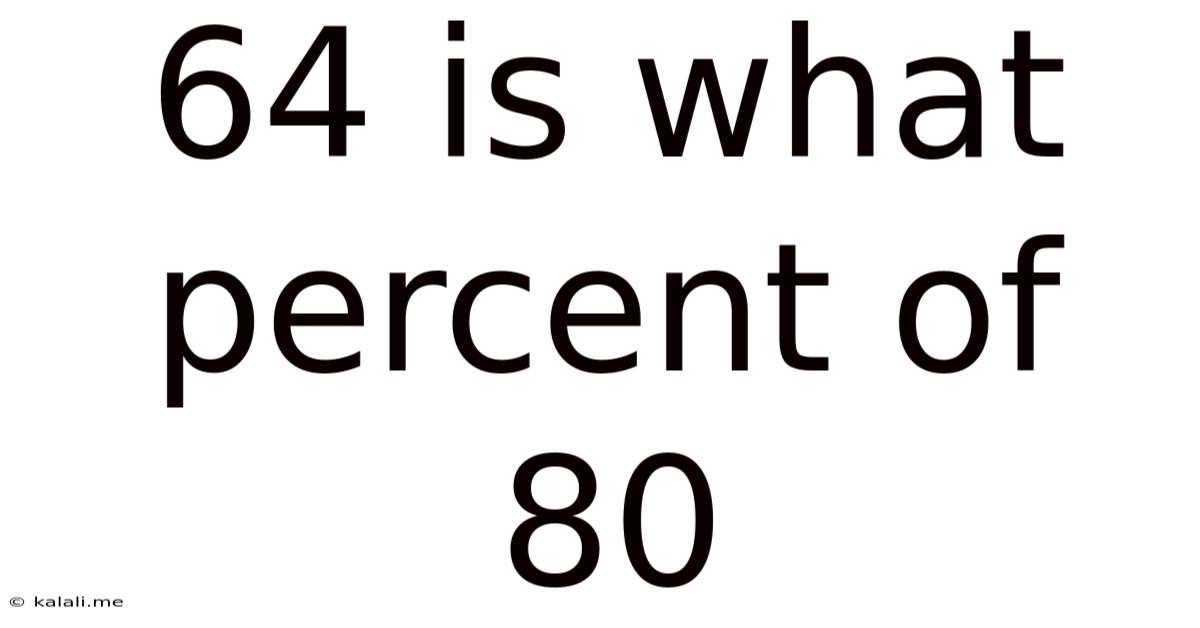
Table of Contents
64 is What Percent of 80? A Comprehensive Guide to Percentage Calculations
This seemingly simple question, "64 is what percent of 80?", opens the door to a world of percentage calculations crucial in various aspects of life, from everyday budgeting and shopping to complex financial analysis and scientific research. Understanding how to solve this, and similar problems, is a foundational skill that empowers you to confidently navigate numerical challenges. This comprehensive guide will not only answer the question but also delve into the underlying principles, provide multiple solution methods, and explore practical applications of percentage calculations.
Meta Description: Learn how to calculate percentages with this in-depth guide. We'll show you multiple ways to solve "64 is what percent of 80?", explain the underlying concepts, and explore practical applications of percentage calculations in various fields.
Understanding Percentages: The Foundation
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred." When we say "x%," we mean x out of every 100. Therefore, understanding percentages involves understanding fractions and proportions. For instance, 50% means 50 out of 100, which simplifies to ½ or 0.5.
The ability to convert between fractions, decimals, and percentages is fundamental to mastering percentage calculations. Remember these key conversions:
- Fraction to Percentage: Divide the numerator by the denominator and multiply by 100. For example, ¾ = (3/4) * 100 = 75%.
- Decimal to Percentage: Multiply the decimal by 100 and add the % symbol. For example, 0.75 = 0.75 * 100 = 75%.
- Percentage to Decimal: Divide the percentage by 100. For example, 75% = 75/100 = 0.75.
- Percentage to Fraction: Write the percentage as a fraction with a denominator of 100, then simplify. For example, 75% = 75/100 = ¾.
Method 1: Using the Proportion Method
This is a classic and intuitive method for solving percentage problems. We set up a proportion, relating the part to the whole, and solve for the unknown percentage.
In our problem, "64 is what percent of 80?", we can set up the proportion as follows:
- Part / Whole = Percentage / 100
Substituting the known values:
- 64 / 80 = x / 100
To solve for x (the unknown percentage), we cross-multiply:
- 64 * 100 = 80 * x
- 6400 = 80x
Now, divide both sides by 80:
- x = 6400 / 80
- x = 80
Therefore, 64 is 80% of 80.
Method 2: Using the Decimal Method
This method involves converting the problem into a decimal equation. We divide the part by the whole to find the decimal equivalent, then convert that decimal to a percentage.
- Divide the part by the whole: 64 / 80 = 0.8
- Convert the decimal to a percentage: 0.8 * 100 = 80%
This method is often quicker and more efficient, especially with simpler problems.
Method 3: Using the Formula Method
A more direct approach involves using the formula:
- Percentage = (Part / Whole) * 100
Substituting the values from our problem:
- Percentage = (64 / 80) * 100
- Percentage = 0.8 * 100
- Percentage = 80%
Practical Applications of Percentage Calculations
Understanding percentage calculations extends far beyond simple mathematical exercises. Here are some real-world applications:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and returns on investment (ROI) all heavily rely on percentage calculations. For example, calculating a 15% discount on a $100 item involves finding 15% of $100, which is $15. The final price would be $85.
-
Shopping: Comparing prices, determining the best deals, and understanding sales discounts require a solid grasp of percentages. For example, comparing two items – one priced at $50 with a 20% discount and another priced at $40 – requires calculating the final price of the discounted item and then comparing it to the other.
-
Science: Percentages are used extensively in scientific research to represent data, express probabilities, and analyze experimental results. For example, expressing the percentage of a certain element in a compound or the success rate of a medical treatment.
-
Statistics: Percentages are crucial in expressing and interpreting statistical data, like the percentage of a population with a certain characteristic or the percentage change in a variable over time. This applies to many fields like demographics, public health and market research.
-
Everyday Life: Calculating tips in restaurants, determining the percentage of a task completed, or understanding the nutritional information on food labels all involve percentage calculations.
Advanced Percentage Problems: Variations and Challenges
While the problem "64 is what percent of 80?" is relatively straightforward, percentage calculations can become more complex. Here are some variations:
-
Finding the whole: If you know the percentage and the part, you can find the whole. For example, "30 is 60% of what number?" requires solving the equation 30 = 0.6x, where x is the whole.
-
Finding the part: If you know the percentage and the whole, you can find the part. For example, "What is 25% of 200?" requires calculating 0.25 * 200.
-
Percentage increase/decrease: These problems involve calculating the percentage change between two values. For example, "A price increased from $50 to $60. What is the percentage increase?" requires calculating [(60-50)/50] * 100 = 20%.
-
Compound percentages: These problems involve calculating percentages on percentages, often found in compound interest calculations.
-
Percentage points: These are not the same as percentages. A percentage point refers to an absolute difference in percentages, not a relative change. For instance, an increase from 10% to 15% is a 5 percentage point increase, but a 50% relative increase.
Mastering Percentage Calculations: Tips and Practice
Mastering percentage calculations takes practice. Here are some tips:
- Understand the underlying concepts: A firm grasp of fractions, decimals, and proportions is essential.
- Practice regularly: Work through various problems, starting with simple ones and gradually increasing the complexity.
- Use multiple methods: Trying different approaches helps reinforce understanding and builds confidence.
- Check your answers: Always double-check your calculations to ensure accuracy.
- Utilize online resources: Numerous websites and apps offer practice problems and tutorials on percentage calculations.
In conclusion, while the answer to "64 is what percent of 80?" is 80%, the true value lies in understanding the underlying principles and applying these skills to a wide range of real-world situations. From budgeting to scientific analysis, the ability to confidently handle percentage calculations is an invaluable skill that enhances problem-solving abilities and empowers informed decision-making.
Latest Posts
Latest Posts
-
1 Out Of 12 Is What Percent
Apr 18, 2025
-
How Many Grams In 4 Kilograms
Apr 18, 2025
-
How Many Cm In 2 5 Meters
Apr 18, 2025
-
What Percent Of 60 Is 39
Apr 18, 2025
-
Cuantos Kilometros Hay En Una Milla
Apr 18, 2025
Related Post
Thank you for visiting our website which covers about 64 Is What Percent Of 80 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.