What Percent Of 60 Is 39
Kalali
Apr 18, 2025 · 5 min read
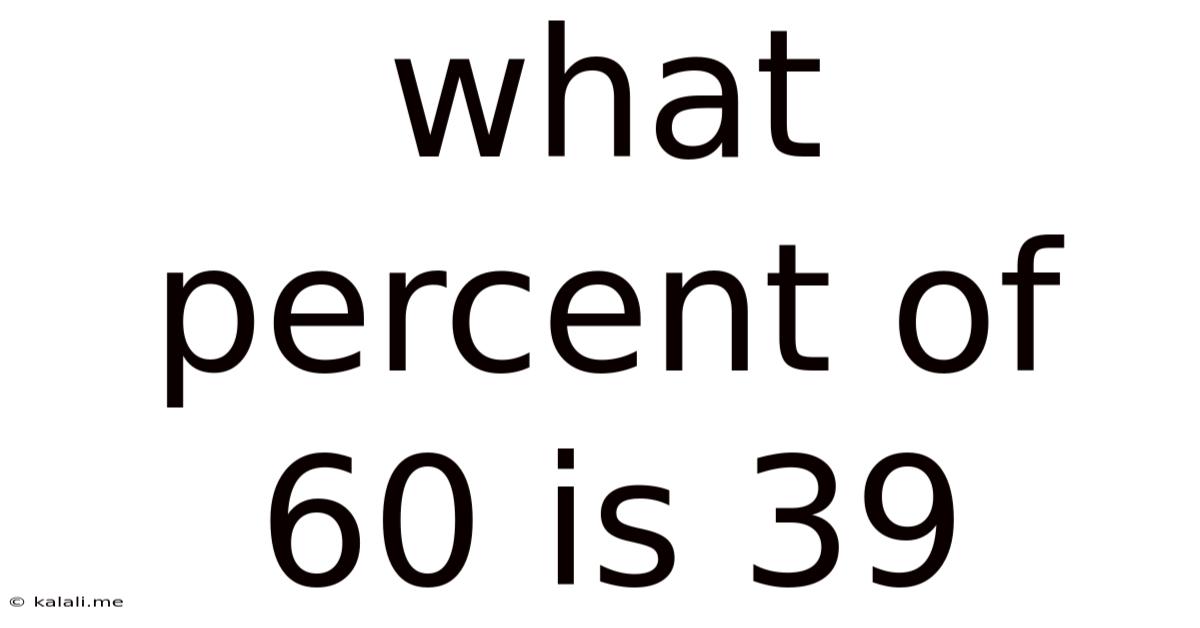
Table of Contents
What Percent of 60 is 39? A Deep Dive into Percentage Calculations
Finding what percent one number represents of another is a fundamental skill in mathematics, crucial for various applications from everyday budgeting to complex statistical analysis. This article will thoroughly explain how to calculate what percentage 39 represents of 60, providing multiple methods and delving into the underlying concepts to ensure a complete understanding. We'll also explore practical examples and offer tips for mastering percentage calculations. This detailed guide will equip you with the knowledge to confidently tackle similar percentage problems.
Understanding Percentages: The Foundation
Before diving into the calculation, let's refresh our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per hundred" or "out of 100". For instance, 50% means 50 out of 100, which simplifies to ½ or 0.5 as a decimal.
The core concept behind percentage calculations is the relationship between three quantities:
- The Part: This is the number we're interested in expressing as a percentage of the whole. In our example, the part is 39.
- The Whole: This is the total or the base number to which the part is compared. In our case, the whole is 60.
- The Percentage: This is the value we want to find, representing the part as a proportion of the whole, expressed as a percentage.
Method 1: Using the Formula
The most straightforward method to determine what percentage 39 is of 60 involves a simple formula:
(Part / Whole) x 100% = Percentage
Substituting our values:
(39 / 60) x 100% = Percentage
- Divide the part by the whole: 39 / 60 = 0.65
- Multiply the result by 100%: 0.65 x 100% = 65%
Therefore, 39 is 65% of 60.
Method 2: Setting up a Proportion
Another way to approach this problem is by setting up a proportion. A proportion expresses the equality of two ratios. We can represent the problem as:
39/60 = x/100
Where 'x' represents the percentage we are trying to find.
To solve this proportion:
- Cross-multiply: 39 * 100 = 60 * x
- Simplify: 3900 = 60x
- Solve for x: x = 3900 / 60 = 65
Therefore, x = 65%, confirming our previous result. This method is particularly useful for visualizing the relationship between the part and the whole.
Method 3: Using Decimal Conversion
We can also solve this problem by first converting the fraction to a decimal and then to a percentage.
- Convert the fraction to a decimal: 39/60 = 0.65
- Convert the decimal to a percentage: 0.65 * 100% = 65%
This method is a simplified version of the first method, directly converting the fraction to a percentage.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is vital in numerous everyday situations:
- Finance: Calculating interest rates, discounts, taxes, tips, and profit margins all rely heavily on percentage calculations. For example, if a store offers a 20% discount on an item priced at $60, you can easily determine the discount amount and the final price using percentage calculations.
- Statistics: Percentages are essential for representing data and drawing conclusions in statistical analysis. Surveys, polls, and research often use percentages to summarize findings and make comparisons. For instance, understanding the percentage of respondents who favored a particular product or candidate is crucial for market research and political analysis.
- Science: Many scientific calculations involve percentages, such as calculating concentrations in chemistry or expressing the relative abundance of different isotopes in physics.
- Everyday Life: From calculating sale prices to understanding nutritional information on food labels, percentage calculations play a significant role in our daily lives.
Advanced Percentage Problems and Variations
While the example of finding what percent 39 is of 60 is relatively straightforward, percentage calculations can become more complex. Here are a few variations:
- Finding the part: If you know the percentage and the whole, you can calculate the part. For example, finding 25% of 80.
- Finding the whole: If you know the percentage and the part, you can calculate the whole. For example, if 30 is 60% of a number, what is that number?
- Percentage increase/decrease: Calculating the percentage change between two numbers. For instance, determining the percentage increase in sales from one year to another.
- Compound percentages: Calculating percentages applied multiple times, such as compound interest.
These more advanced problems require slightly modified formulas but build upon the fundamental principles outlined in this article.
Tips for Mastering Percentage Calculations
- Practice Regularly: Consistent practice is key to mastering percentage calculations. Start with simple problems and gradually work your way up to more complex ones.
- Understand the Concepts: Focus on understanding the underlying concepts of percentages and their relationship to fractions and decimals.
- Use Multiple Methods: Trying different methods to solve the same problem can strengthen your understanding and improve your problem-solving skills.
- Check Your Answers: Always double-check your calculations to ensure accuracy.
- Utilize Online Resources: Several online resources, calculators, and tutorials can help you practice and improve your understanding of percentages.
Conclusion
In conclusion, 39 is 65% of 60. This article has explored various methods for calculating percentages, highlighted real-world applications, and touched upon more complex percentage problems. By understanding the fundamental principles and practicing regularly, you can confidently tackle any percentage calculation you encounter. Remember, mastering percentages is a valuable skill that will serve you well in many aspects of life. So, continue practicing, explore different problem types, and confidently apply your newfound knowledge to solve percentage problems effectively.
Latest Posts
Latest Posts
-
14 Of 20 As A Percentage
Apr 22, 2025
-
What Is 30 Out Of 41
Apr 22, 2025
-
What Is The Reciprocal Of 6
Apr 22, 2025
-
At What Temperature Does Blood Boil
Apr 22, 2025
-
What Is 8 12 As A Percentage
Apr 22, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 60 Is 39 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.