69 Out Of 75 As A Percentage
Kalali
Aug 23, 2025 · 5 min read
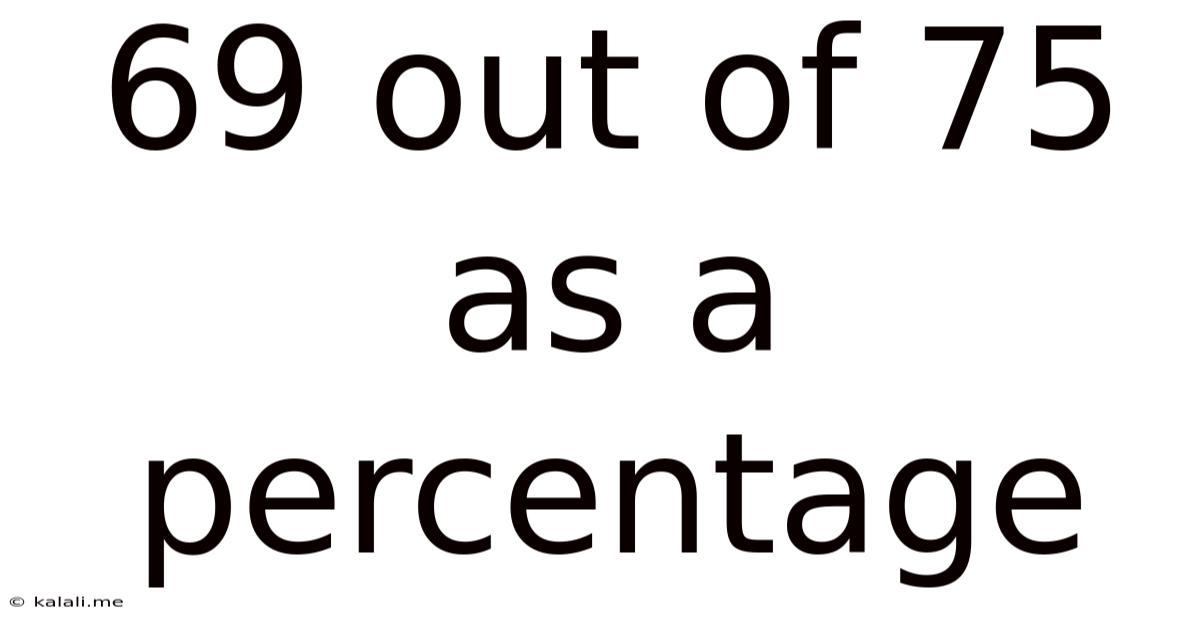
Table of Contents
69 out of 75 as a Percentage: A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill applicable across numerous fields, from academic assessments to financial analysis and everyday life. Understanding how to convert fractions into percentages is crucial for interpreting data and making informed decisions. This article delves into the specific calculation of 69 out of 75 as a percentage, exploring the underlying methodology and offering practical applications. We'll also cover common methods, potential errors, and how to use this knowledge in various contexts.
Understanding Percentages: A Quick Refresher
Before diving into the specifics of 69 out of 75, let's briefly review the concept of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For example, 50% means 50 out of 100, which is equivalent to ½ or 0.5.
Calculating 69 out of 75 as a Percentage: The Step-by-Step Method
The most straightforward way to calculate 69 out of 75 as a percentage involves the following steps:
-
Form a Fraction: Express the given numbers as a fraction: 69/75. This represents the part (69) over the whole (75).
-
Convert the Fraction to a Decimal: Divide the numerator (69) by the denominator (75): 69 ÷ 75 = 0.92
-
Convert the Decimal to a Percentage: Multiply the decimal by 100 and add the percentage symbol (%): 0.92 x 100 = 92%
Therefore, 69 out of 75 is equal to 92%.
Alternative Methods for Percentage Calculation
While the above method is the most common and arguably the simplest, alternative approaches can be employed, especially when dealing with more complex scenarios or using different tools:
-
Using a Calculator: Most calculators have a percentage function that simplifies the process. Simply enter 69 ÷ 75 and then multiply by 100. The calculator will directly provide the answer as 92%.
-
Using Spreadsheet Software: Spreadsheet programs like Microsoft Excel or Google Sheets offer built-in functions for percentage calculations. For example, in Excel, you could use the formula
=69/75*100in a cell to obtain the result. -
Using Online Percentage Calculators: Numerous online tools are available that can perform percentage calculations quickly and accurately. Simply input the values, and the calculator will return the percentage. These calculators are particularly useful for quick calculations or when you don't have access to a calculator or spreadsheet software.
Practical Applications of Percentage Calculations
The ability to calculate percentages has widespread applications across numerous fields:
-
Academic Performance: Calculating grades, test scores, and overall academic performance frequently involves percentage calculations. For example, a student scoring 69 out of 75 on a test achieved a 92% grade.
-
Financial Analysis: Percentages are crucial in analyzing financial data, including calculating interest rates, profit margins, growth rates, and investment returns. Understanding percentage changes helps in making informed financial decisions.
-
Business and Marketing: Percentages are used extensively in business to analyze sales figures, market share, customer satisfaction, and advertising effectiveness. For instance, a company might track the percentage of website visitors who make a purchase.
-
Data Analysis and Statistics: Percentages are fundamental in statistical analysis for presenting and interpreting data in a clear and concise manner. They enable comparisons between different data sets and facilitate the identification of trends.
-
Everyday Life: We encounter percentages in various daily scenarios, such as calculating discounts, sales tax, tips, and understanding proportions in recipes or measurements.
Potential Errors and How to Avoid Them
While percentage calculations are relatively straightforward, common errors can arise if caution isn't exercised:
-
Incorrect Order of Operations: Ensure the division is performed before the multiplication when converting the fraction to a percentage.
-
Decimal Point Errors: Double-check the decimal point placement when converting between decimals and percentages. A misplaced decimal point can significantly alter the result.
-
Incorrect Interpretation of the Question: Always carefully read the problem statement to identify the part and the whole accurately. Ensure you are calculating the correct percentage.
-
Rounding Errors: When rounding off the final answer, be mindful of the required level of precision. Rounding too early can introduce inaccuracies.
Expanding on the Calculation: Understanding the Context
The 92% derived from 69 out of 75 provides valuable information, but its interpretation depends heavily on context. For example:
-
In an exam context: A score of 92% is generally considered excellent. It indicates a strong understanding of the subject matter.
-
In a business context: A 92% success rate for a marketing campaign might suggest a highly effective strategy. However, a 92% defect rate in a manufacturing process would be disastrous and require immediate attention.
-
In a statistical analysis: 92% could represent a high level of correlation between two variables, indicating a strong relationship.
Beyond the Basics: Working with More Complex Percentage Problems
While 69 out of 75 is a relatively simple percentage calculation, the principles can be extended to more complex scenarios. For instance:
-
Calculating Percentage Increase or Decrease: This involves determining the percentage change between two values. For example, if a value increases from 75 to 69, the percentage decrease can be calculated.
-
Calculating Percentage Points: This refers to the absolute difference between two percentages. For instance, if the market share of a product increases from 69% to 75%, the increase is 6 percentage points, not 6%.
-
Calculating Percentages of Percentages: This involves calculating a percentage of a percentage value. For example, finding 10% of 92%.
Conclusion:
Calculating 69 out of 75 as a percentage provides a clear illustration of a fundamental mathematical skill. The result, 92%, is easily obtained through several methods, and its significance hinges on the specific application. Understanding percentages is not merely a mathematical exercise; it's a crucial tool for interpreting data, making informed decisions, and achieving success across various aspects of life and work. By mastering percentage calculations and understanding their applications, you gain a valuable skill that enhances your analytical abilities and problem-solving skills. Remember to always double-check your calculations and consider the context when interpreting the results. This understanding will help you confidently tackle more complex percentage problems and extract meaningful insights from data.
Latest Posts
Latest Posts
-
The Trickiest And Most Difficult Lighting Exists
Aug 24, 2025
-
What Does On View Mean In Jail
Aug 24, 2025
-
Seven Less Than A Number Is 15
Aug 24, 2025
-
250 Mm Is Equal To How Many Inches
Aug 24, 2025
-
How Long Does Your Pores Stay Open After A Shower
Aug 24, 2025
Related Post
Thank you for visiting our website which covers about 69 Out Of 75 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.