7 5 As A Mixed Number
Kalali
Apr 13, 2025 · 5 min read
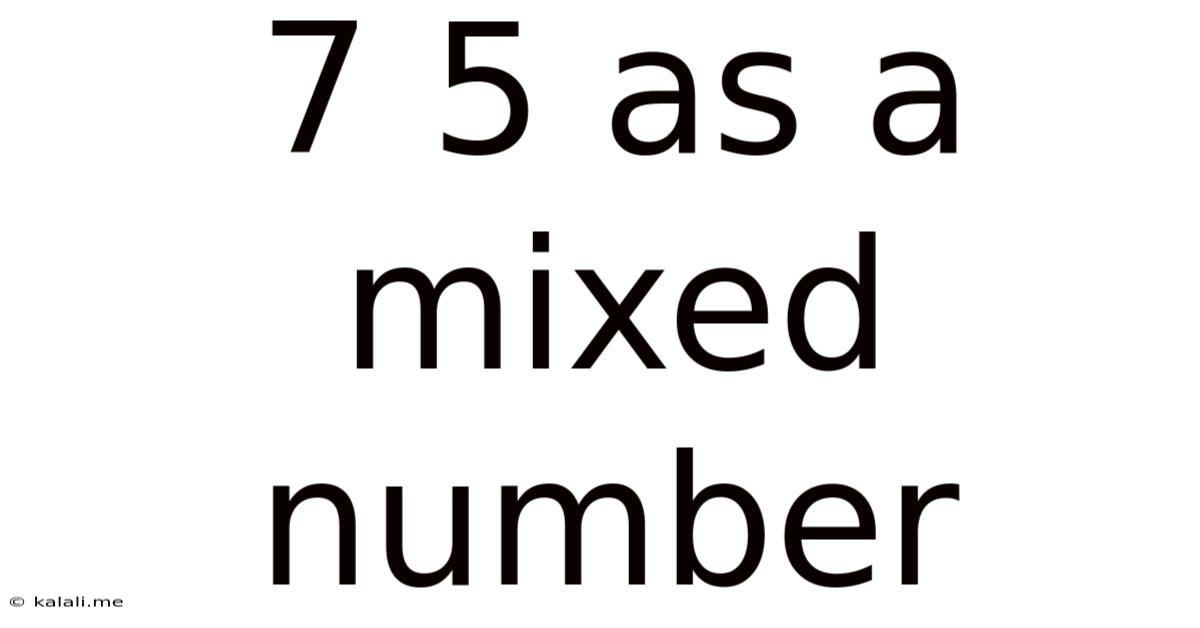
Table of Contents
Decoding 7 5/1: Understanding Mixed Numbers and Improper Fractions
The seemingly simple expression "7 5/1" might appear straightforward at first glance, but it opens a door to a fundamental concept in mathematics: understanding the relationship between mixed numbers and improper fractions. This article delves deep into the meaning of 7 5/1, exploring its conversion to an improper fraction, its representation on a number line, and its applications in real-world scenarios. We'll also explore related concepts like simplifying fractions and working with mixed numbers in various mathematical operations. This comprehensive guide aims to solidify your understanding of this core mathematical principle.
What is a Mixed Number?
A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator (the top number) is smaller than the denominator (the bottom number). In the case of 7 5/1, the whole number is 7 and the fraction is 5/1.
What is an Improper Fraction?
An improper fraction is a fraction where the numerator is greater than or equal to the denominator. This indicates a value greater than or equal to one. While 5/1 is technically an improper fraction, it's a crucial stepping stone to understanding the conversion process.
Understanding 7 5/1: The Significance of the Fraction 5/1
The fraction 5/1 in 7 5/1 represents five wholes divided into one part each. This simplifies to 5. Therefore, 7 5/1 can be interpreted as 7 + 5/1 = 7 + 5 = 12.
Converting Mixed Numbers to Improper Fractions: A Step-by-Step Guide
Converting a mixed number like 7 5/1 to an improper fraction is a crucial skill. Here's how it's done:
- Multiply the whole number by the denominator: 7 * 1 = 7
- Add the numerator to the result: 7 + 5 = 12
- Keep the same denominator: The denominator remains 1.
- The resulting improper fraction is: 12/1
Therefore, 7 5/1 is equivalent to the improper fraction 12/1. This conversion is essential for performing various mathematical operations, especially when dealing with fractions in equations or problems involving multiple mixed numbers.
Converting Improper Fractions to Mixed Numbers
The reverse process, converting an improper fraction to a mixed number, is equally important. Let's take the example of 12/1:
- Divide the numerator by the denominator: 12 ÷ 1 = 12
- The quotient becomes the whole number: The whole number is 12.
- The remainder becomes the numerator: There is no remainder in this case (12 divided by 1 is 12 with no remainder). This signifies that the fractional part is 0/1, which simplifies to 0.
- The denominator remains the same: The denominator is still 1.
- The resulting mixed number is: 12 0/1, which simplifies to 12.
Visual Representation on a Number Line
Visualizing 7 5/1 (or 12) on a number line reinforces the understanding of its value. You would simply locate the point corresponding to the number 12 on the number line. The number line provides a concrete representation of the position of this number relative to other numbers.
Real-World Applications of Mixed Numbers and Improper Fractions
Mixed numbers and improper fractions are not just abstract mathematical concepts; they have numerous practical applications in everyday life. Consider these examples:
-
Cooking and Baking: Recipes often use mixed numbers to specify ingredient quantities, such as 2 1/2 cups of flour or 1 3/4 teaspoons of baking powder. Converting these to improper fractions can be useful for precise calculations when scaling up or down a recipe.
-
Measurement: Measuring lengths, weights, or volumes often involves mixed numbers. For instance, a board might measure 5 3/4 feet long, or a container might hold 1 2/3 gallons of liquid.
-
Construction and Engineering: Precise measurements are crucial in construction and engineering. Mixed numbers and improper fractions are frequently used to express dimensions and quantities.
-
Finance: Calculations involving monetary amounts can involve fractions, especially when dealing with interest rates, taxes, or portions of investments.
-
Data Analysis and Statistics: When working with averages, proportions, or percentages, it's common to encounter situations where mixed numbers or improper fractions are necessary for representation or calculation.
Simplifying Fractions: A Necessary Skill
Before performing calculations with fractions, especially when dealing with larger numbers, simplifying them is crucial. A simplified fraction is a fraction reduced to its lowest terms. This means the greatest common divisor (GCD) of the numerator and the denominator is 1.
For example, let’s say we had the fraction 12/6. The GCD of 12 and 6 is 6. Dividing both the numerator and denominator by 6 simplifies this fraction to 2/1, which is equivalent to 2. Simplifying fractions makes calculations easier and results more manageable.
Operations with Mixed Numbers
Adding, subtracting, multiplying, and dividing mixed numbers requires converting them to improper fractions first, simplifying, and then converting back into mixed numbers for the final answer. Let's illustrate with an example of addition:
Add 2 1/2 and 3 3/4.
- Convert to improper fractions: 2 1/2 = 5/2 and 3 3/4 = 15/4
- Find a common denominator: The common denominator for 2 and 4 is 4.
- Rewrite the fractions with the common denominator: 5/2 = 10/4
- Add the fractions: 10/4 + 15/4 = 25/4
- Convert back to a mixed number: 25/4 = 6 1/4
Advanced Applications and Further Exploration
The concepts of mixed numbers and improper fractions form the foundation for more advanced mathematical concepts. Understanding these principles is crucial for success in algebra, calculus, and other higher-level mathematics. Further exploration might involve examining the use of mixed numbers and improper fractions in geometry, probability, and statistics.
Conclusion
While 7 5/1 might seem deceptively simple, it serves as a powerful illustration of the relationship between mixed numbers and improper fractions. Mastering the conversion between these forms is vital for a strong foundation in mathematics, allowing you to tackle more complex problems and confidently apply these concepts across numerous disciplines. From everyday tasks to advanced mathematical calculations, the ability to work fluently with mixed numbers and improper fractions is an invaluable skill. Remember to practice regularly, utilizing various examples and real-world applications to solidify your understanding. The more you practice, the more intuitive and comfortable you will become with these fundamental mathematical tools.
Latest Posts
Latest Posts
-
Cuanto Es 19 Libras En Kilos
Apr 14, 2025
-
How Long Is 19 Inches In Cm
Apr 14, 2025
-
What Is 400 Ml In Oz
Apr 14, 2025
-
What Is 18 30 As A Percentage
Apr 14, 2025
-
Lewis Structure Correctly Represents Strontium Chloride
Apr 14, 2025
Related Post
Thank you for visiting our website which covers about 7 5 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.