7 Out Of 13 As A Percentage
Kalali
Apr 27, 2025 · 5 min read
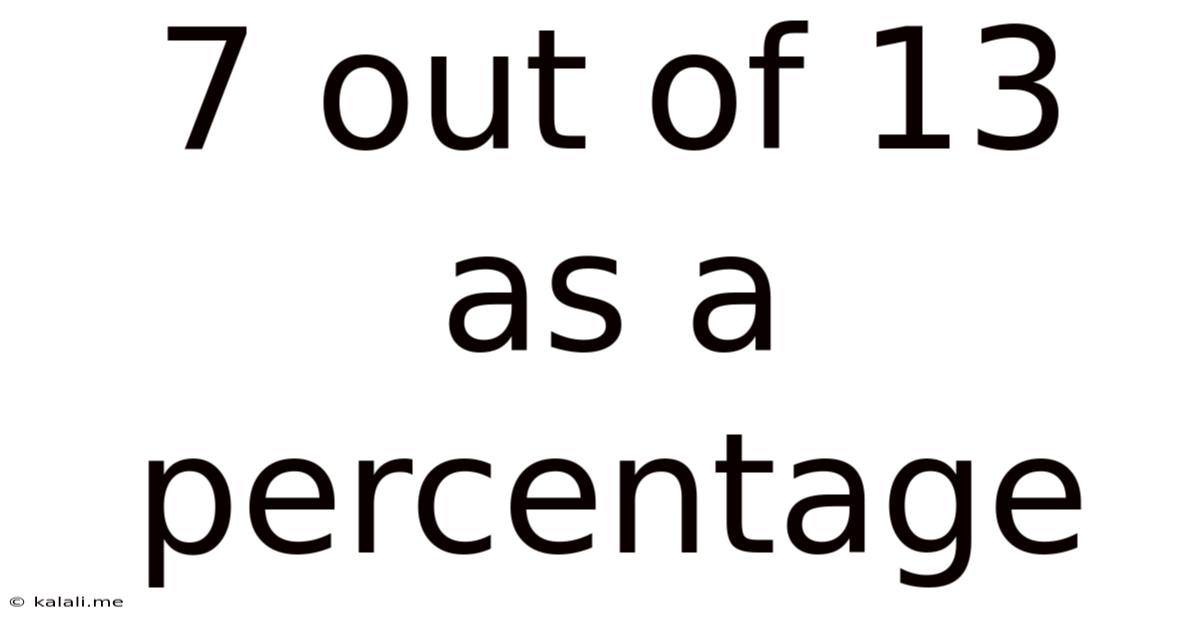
Table of Contents
Decoding the Fraction: 7 out of 13 as a Percentage and Beyond
Understanding fractions and converting them into percentages is a fundamental skill with applications spanning various fields, from everyday budgeting to complex scientific calculations. This article delves deep into the conversion of the fraction 7/13 into a percentage, exploring the underlying methodology, providing practical examples, and examining the broader context of percentage calculations. We'll also look at how to round percentages, the importance of accuracy, and applications beyond simple conversions.
Meta Description: Learn how to convert 7 out of 13 into a percentage. This comprehensive guide explains the process, explores rounding, discusses accuracy, and offers real-world applications of percentage calculations.
Understanding Fractions and Percentages
Before diving into the specific calculation, let's establish a solid understanding of the concepts involved. A fraction represents a part of a whole. It's expressed as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). In our case, the fraction is 7/13, meaning 7 parts out of a total of 13 parts.
A percentage, denoted by the symbol %, represents a fraction of 100. It indicates how many parts out of 100 comprise a given portion. Converting a fraction to a percentage involves expressing the fraction as an equivalent fraction with a denominator of 100, or alternatively, multiplying the fraction by 100%.
Calculating 7 out of 13 as a Percentage: The Step-by-Step Guide
The most straightforward method to convert 7/13 into a percentage involves the following steps:
-
Divide the numerator by the denominator: Divide 7 by 13. This calculation yields a decimal value: 7 ÷ 13 ≈ 0.53846
-
Multiply the decimal by 100: To express this decimal as a percentage, multiply the result from step 1 by 100. 0.53846 x 100 = 53.846
-
Add the percentage symbol: Finally, add the percentage symbol (%) to indicate that the result represents a percentage. Therefore, 7 out of 13 is approximately 53.846%.
Rounding Percentages: Precision vs. Practicality
The result we obtained, 53.846%, contains three decimal places. Depending on the context, this level of precision may or may not be necessary. Rounding allows us to simplify the percentage while maintaining an acceptable level of accuracy.
Common rounding practices include:
-
Rounding to the nearest whole number: In this case, 53.846% would round to 54%. This is suitable for situations where a rough estimate is sufficient.
-
Rounding to one decimal place: Rounding to one decimal place yields 53.8%. This offers a balance between simplicity and accuracy.
-
Rounding to two decimal places: This gives us 53.85%. This provides a higher level of accuracy than rounding to one decimal place.
The choice of how many decimal places to round to depends largely on the specific application. For instance, in a financial context, higher precision is often preferred, whereas in a general overview, rounding to the nearest whole number might suffice.
Understanding the Importance of Accuracy
While rounding can simplify percentages, it’s crucial to understand the implications of rounding errors. In many applications, especially those involving financial calculations, small errors can accumulate and significantly impact the final result. Therefore, understanding the level of accuracy required for a specific task is paramount.
Consider the following scenarios:
-
Calculating a discount: If a store offers a discount of 53.846%, rounding down to 53% might save the store money, but could lead to customer dissatisfaction if they expect the higher discount.
-
Analyzing statistical data: In scientific studies, precise percentages are essential for drawing accurate conclusions. Rounding errors in this context could lead to flawed interpretations of the data.
-
Project budgeting: In project management, accuracy is key to ensuring sufficient funds are allocated to complete the project successfully. Incorrect percentage calculations can lead to budget overruns or shortfalls.
Real-World Applications of Percentage Calculations
The conversion of fractions to percentages finds widespread application across numerous fields:
-
Finance: Calculating interest rates, profit margins, tax rates, and discounts are all based on percentage calculations.
-
Statistics: Expressing data as percentages allows for easier comparison and interpretation of data sets.
-
Science: Percentage calculations are vital in chemistry, physics, and biology for expressing concentrations, yields, and error margins.
-
Everyday life: Calculating tips in restaurants, understanding sales tax, and interpreting survey results all involve percentage calculations.
Beyond 7 out of 13: Mastering Percentage Conversions
The method outlined above for converting 7/13 to a percentage is applicable to any fraction. To convert any fraction (a/b) to a percentage, follow these steps:
- Divide the numerator (a) by the denominator (b).
- Multiply the result by 100.
- Add the percentage symbol (%).
For example, let's convert 5/8 to a percentage:
- 5 ÷ 8 = 0.625
- 0.625 x 100 = 62.5
- Therefore, 5/8 is equal to 62.5%.
Using Calculators and Software for Percentage Calculations
While manual calculation provides a thorough understanding of the process, calculators and software offer efficiency and accuracy, especially for complex calculations. Most calculators have a percentage function that directly converts fractions or decimals into percentages. Spreadsheet software like Microsoft Excel or Google Sheets also provides built-in functions for percentage calculations, making complex analyses significantly easier.
Advanced Percentage Calculations: Finding the Whole from a Percentage
Often, we need to work backwards, calculating the whole amount based on a percentage and a part. For example, if 7 out of 13 represents 53.85% (approximately), and we know this 53.85% corresponds to a value of $70, we can find the total value by setting up a simple equation:
0.5385 * x = 70
Solving for x (the total value) gives us:
x = 70 / 0.5385 ≈ $130
This demonstrates the practical application of percentage calculations in solving real-world problems.
Conclusion: The Power of Percentage Understanding
The seemingly simple conversion of 7 out of 13 into a percentage showcases the fundamental importance of understanding fractions and percentages. From everyday financial transactions to advanced scientific research, the ability to perform and interpret percentage calculations is an essential skill. This article has provided a comprehensive guide, emphasizing the process, the significance of accuracy, and the practical applications of percentage conversions, equipping you with the knowledge to confidently navigate various scenarios involving percentages. Remember to always consider the context and required level of precision when rounding your results.
Latest Posts
Latest Posts
-
What Is 25 Percent Of 75
Apr 27, 2025
-
How Many Cm In 6 Meters
Apr 27, 2025
-
Is 83 A Prime Number Or A Composite Number
Apr 27, 2025
-
Cuanto Es 1 4 De Taza En Onzas
Apr 27, 2025
-
What Are Prime Factors Of 14
Apr 27, 2025
Related Post
Thank you for visiting our website which covers about 7 Out Of 13 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.