What Is 25 Percent Of 75
Kalali
Apr 27, 2025 · 5 min read
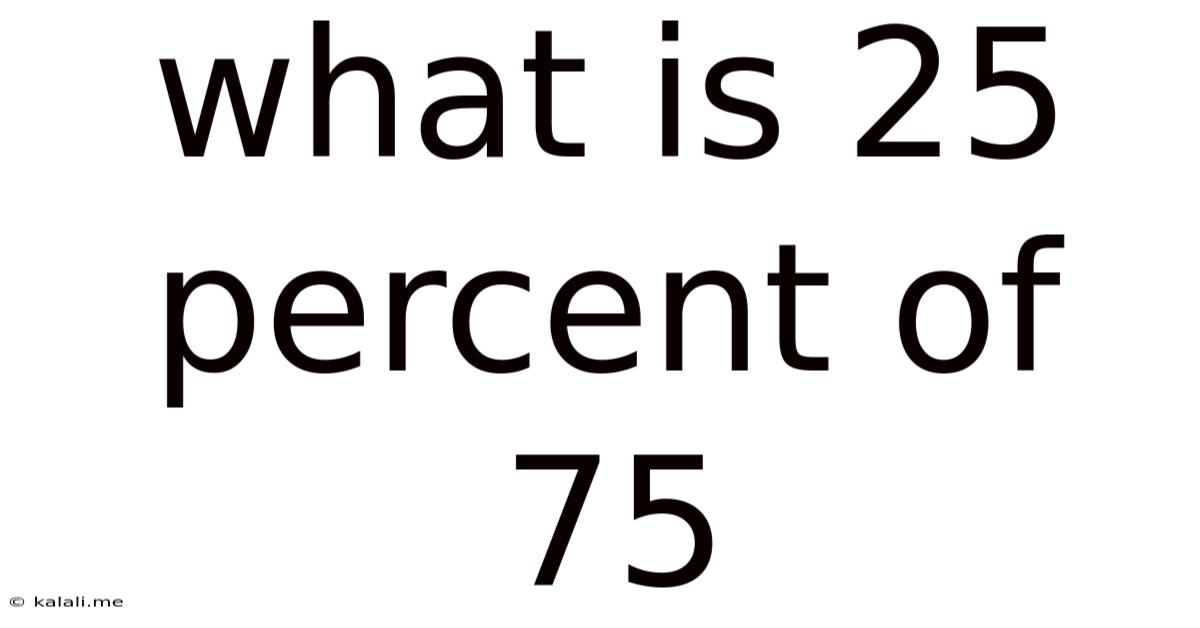
Table of Contents
What is 25 Percent of 75? A Deep Dive into Percentages and Their Applications
This seemingly simple question, "What is 25 percent of 75?", opens a door to a vast world of mathematical concepts with far-reaching applications in everyday life, finance, and various fields. Understanding percentages is crucial for making informed decisions, from calculating discounts and taxes to interpreting statistical data and understanding financial reports. This article will not only answer the initial question but also explore the underlying principles of percentage calculations, different methods to solve percentage problems, and real-world examples demonstrating their significance.
Meta Description: Learn how to calculate 25% of 75 and delve into the broader world of percentages. This comprehensive guide covers various methods, real-world applications, and practical tips for mastering percentage calculations.
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "percent," which literally means "out of one hundred." Therefore, 25% means 25 out of 100, or 25/100, which simplifies to 1/4. This fundamental understanding is key to solving any percentage problem.
Calculating 25% of 75: Three Different Approaches
There are several ways to calculate 25% of 75. Let's explore three common methods:
1. The Fraction Method:
This method leverages the fractional equivalent of a percentage. As mentioned earlier, 25% is equal to 1/4. Therefore, finding 25% of 75 is the same as finding 1/4 of 75:
75 x (1/4) = 75/4 = 18.75
Therefore, 25% of 75 is 18.75.
2. The Decimal Method:
This method converts the percentage to a decimal before performing the calculation. To convert a percentage to a decimal, divide the percentage by 100. 25% divided by 100 is 0.25. Then, multiply this decimal by the number:
75 x 0.25 = 18.75
Again, 25% of 75 is 18.75.
3. The Proportion Method:
This method sets up a proportion to solve for the unknown value. A proportion is an equation that states two ratios are equal. We can set up the proportion as follows:
25/100 = x/75
To solve for x (which represents 25% of 75), cross-multiply:
25 * 75 = 100 * x 1875 = 100x x = 1875/100 x = 18.75
Once again, we find that 25% of 75 is 18.75.
Real-World Applications of Percentage Calculations
Percentage calculations are ubiquitous in daily life and various professional settings. Here are a few examples:
-
Retail Discounts: Stores frequently offer discounts advertised as percentages. For example, a "25% off" sale means you pay 75% of the original price. Understanding percentage calculations is crucial to determining the final price after a discount.
-
Taxes and Interest: Sales tax, income tax, and interest rates are all expressed as percentages. Calculating these amounts accurately requires a solid understanding of percentage calculations. For instance, calculating the total cost of an item including sales tax involves adding the percentage of tax to the original price.
-
Financial Planning: Percentages are fundamental to understanding financial statements, investment returns, and loan calculations. Calculating interest earned on savings accounts or the monthly payments on a loan involves working with percentages.
-
Statistical Analysis: Percentages are widely used to represent data in various fields, from market research and demographics to scientific studies and public health statistics. Understanding percentages helps interpret the meaning and significance of these data.
-
Grade Calculation: Many educational systems use percentages to represent student grades. Calculating a final grade often involves weighted averages, which rely on percentage calculations.
-
Tip Calculation: Calculating a tip at a restaurant often involves determining a percentage of the bill amount.
Beyond the Basics: Advanced Percentage Problems
While calculating 25% of 75 is relatively straightforward, more complex percentage problems require a deeper understanding of the underlying concepts. Here are a few examples:
-
Finding the Percentage: Instead of finding a percentage of a number, you might need to determine what percentage one number represents of another. For example, what percentage is 15 of 60? This requires setting up a proportion or dividing 15 by 60 and multiplying by 100.
-
Finding the Original Amount: You might know the percentage increase or decrease and the final amount and need to calculate the original amount. For instance, if a price increased by 10% to $110, what was the original price?
-
Compound Interest: Compound interest involves calculating interest on both the principal amount and accumulated interest. These calculations require understanding exponential growth and can be more complex than simple percentage calculations.
-
Percentage Change: Determining the percentage increase or decrease between two values is crucial in many applications, including analyzing trends in sales figures, population growth, or stock market fluctuations.
Tips and Tricks for Mastering Percentage Calculations
-
Memorize common percentage equivalents: Knowing that 25% = 1/4, 50% = 1/2, and 75% = 3/4 can significantly speed up calculations.
-
Use a calculator: For more complex calculations, a calculator is a valuable tool. Many calculators have a percentage function that simplifies the process.
-
Break down complex problems: Large or complex percentage problems can often be broken down into smaller, more manageable steps.
-
Practice regularly: The best way to master percentage calculations is to practice regularly. Start with simple problems and gradually increase the difficulty.
Conclusion: The Power of Percentages
Understanding percentages is a fundamental skill with broad applications across various fields. From everyday shopping to complex financial analysis, the ability to accurately calculate and interpret percentages is essential for making informed decisions and navigating the numerical world effectively. While calculating 25% of 75 might seem insignificant on its own, mastering this basic concept lays the groundwork for tackling more complex percentage problems and utilizing this crucial mathematical tool in your personal and professional life. The simple answer, 18.75, unlocks a world of understanding and capability.
Latest Posts
Latest Posts
-
What Is 10 Percent Of 1300
Apr 27, 2025
-
30 Feet Equals How Many Meters
Apr 27, 2025
-
4 Is What Percent Of 30
Apr 27, 2025
-
What Percentage Is 6 Out Of 20
Apr 27, 2025
-
What Percent Of 100 Is 6
Apr 27, 2025
Related Post
Thank you for visiting our website which covers about What Is 25 Percent Of 75 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.