8 6 9 5 10 4 11
Kalali
Jul 29, 2025 · 6 min read
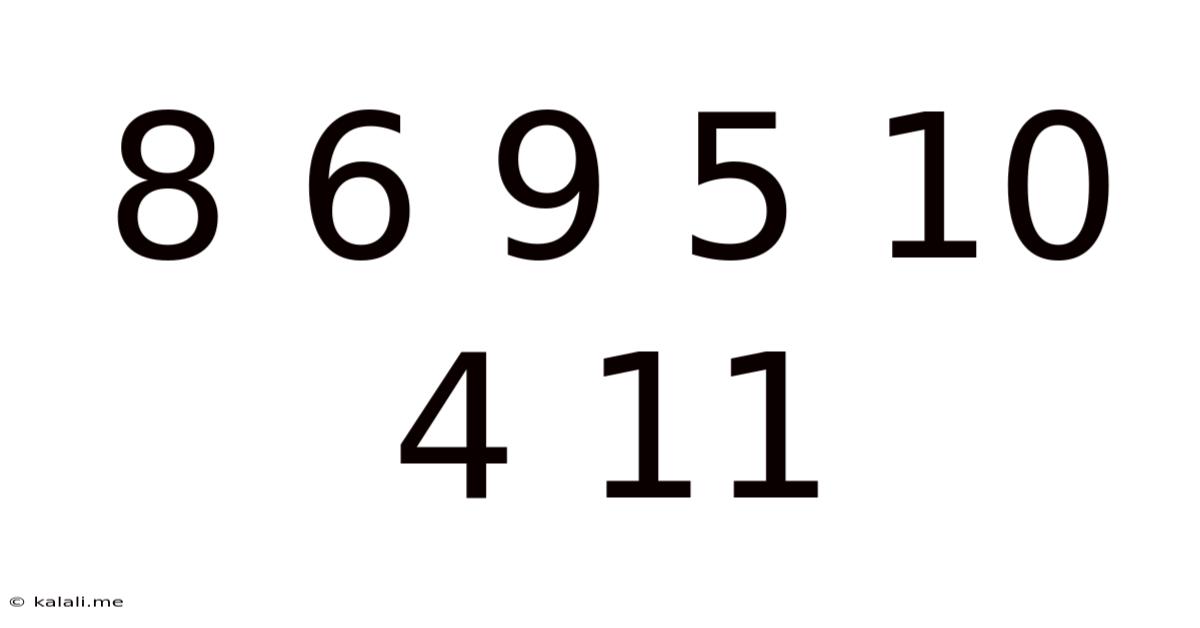
Table of Contents
Decoding the Sequence: 8 6 9 5 10 4 11 – A Deep Dive into Pattern Recognition and Mathematical Series
This article explores the seemingly random sequence 8 6 9 5 10 4 11, delving into various methods of pattern recognition and mathematical series to uncover potential underlying structures. We'll examine different approaches, discuss their limitations, and ultimately consider the inherent ambiguity in interpreting numerical sequences without additional context. The seemingly simple sequence offers a surprisingly rich playground for exploring mathematical thinking and problem-solving strategies. Understanding this requires a blend of logical deduction, creative thinking, and an awareness of common mathematical patterns.
Meta Description: This article analyzes the numerical sequence 8, 6, 9, 5, 10, 4, 11, exploring various mathematical patterns and series to uncover potential underlying structures. We'll investigate different approaches, discuss their limitations, and highlight the challenges of interpreting sequences without context.
The Illusion of Randomness: Initial Observations
At first glance, the sequence 8, 6, 9, 5, 10, 4, 11 appears arbitrary. There's no immediately obvious arithmetic progression or geometric sequence. The numbers fluctuate, seemingly without a consistent rule. This initial impression of randomness is a common starting point when tackling such problems. However, the absence of a clear, simple pattern doesn't necessarily mean the sequence lacks structure; it simply means the structure might be more complex or subtle.
Methodical Approaches: Exploring Different Patterns
To decipher the sequence, we need to employ systematic methods. Several approaches can be taken, each with its own strengths and weaknesses:
1. Differencing: Analyzing the Differences Between Consecutive Terms
A standard technique in sequence analysis is to calculate the differences between consecutive terms. Let's apply this to our sequence:
- 6 - 8 = -2
- 9 - 6 = 3
- 5 - 9 = -4
- 10 - 5 = 5
- 4 - 10 = -6
- 11 - 4 = 7
The differences (-2, 3, -4, 5, -6, 7) themselves don't immediately reveal a clear pattern. However, notice that the absolute values (2, 3, 4, 5, 6, 7) form a simple arithmetic progression. This suggests a potential underlying structure, even though the signs alternate. This method hints at a possible recursive relationship, where the next difference is determined by the previous one with a change in sign.
2. Alternating Subsequences: Breaking Down the Sequence
Another strategy is to consider alternating subsequences. We can split the sequence into two subsequences:
- Subsequence 1: 8, 9, 10, 11 (an arithmetic progression with a common difference of 1)
- Subsequence 2: 6, 5, 4 (an arithmetic progression with a common difference of -1)
This approach reveals a simple pattern within each subsequence. However, the connection between the two subsequences remains unclear. The alternating nature suggests a potential rule that switches between two distinct arithmetic progressions.
3. Modulo Arithmetic: Exploring Remainders
Exploring modulo arithmetic can sometimes reveal hidden patterns. Let's examine the remainders when each term is divided by a small integer, such as 3:
- 8 mod 3 = 2
- 6 mod 3 = 0
- 9 mod 3 = 0
- 5 mod 3 = 2
- 10 mod 3 = 1
- 4 mod 3 = 1
- 11 mod 3 = 2
While the remainders don't immediately form a clear pattern, exploring modulo operations with different divisors might uncover a hidden relationship. This method requires more exploration and experimentation with various divisors.
4. Prime Numbers and Composites: Investigating Number Properties
Another avenue to explore is the properties of the numbers themselves. Let's consider whether the numbers are prime or composite:
- 8 (composite)
- 6 (composite)
- 9 (composite)
- 5 (prime)
- 10 (composite)
- 4 (composite)
- 11 (prime)
The alternation between prime and composite numbers could be relevant, but without a more defined pattern, this observation alone is insufficient to definitively determine the sequence's rule.
The Limitations of Purely Mathematical Approaches
The analysis above demonstrates several methods of exploring numerical sequences. However, we encounter limitations:
- Multiple Possible Solutions: Multiple rules could potentially generate the same initial sequence. Without further data, it's impossible to definitively determine the "correct" rule. Our observations might be coincidental patterns rather than fundamental rules governing the sequence.
- Overfitting: Overfitting occurs when a complex rule is created to perfectly match a small data set. This rule might not accurately predict future terms. A simpler rule might be more robust, even if it doesn't perfectly fit the existing data.
- Context is Crucial: The absence of context makes it difficult to definitively interpret the sequence. If this sequence represents something else (e.g., data points from a scientific experiment, codes, etc.), the interpretation could be completely different.
Beyond Mathematics: Considering Other Possibilities
The lack of a clear mathematical pattern highlights the need to consider other possibilities. The sequence could represent:
- Encoded Information: The numbers might be a code, where each number represents a letter or symbol. Without a key, deciphering this code is impossible.
- Data Points: The sequence could be a subset of a larger data set. The full context might reveal the underlying pattern.
- Random Number Generation: The sequence could be completely random, generated by a random number generator or other stochastic process.
The Importance of Context and Further Information
The inherent ambiguity in interpreting the sequence 8, 6, 9, 5, 10, 4, 11 underscores the crucial role of context in pattern recognition. Without additional information – whether it's more terms in the sequence, a description of the sequence's origin, or a clue about its purpose – we can only speculate about its underlying structure.
To definitively "solve" the sequence, we need more data. For example, if the next few terms were provided, we could test our hypothesized rules and determine which ones best predict the continuation of the sequence. This iterative process of hypothesis generation, testing, and refinement is essential in pattern recognition.
Conclusion: The Value of Exploration and Problem-Solving
Even though we haven't found a definitive, universally accepted rule for the sequence 8 6 9 5 10 4 11, the exploration itself is valuable. This exercise highlights the importance of:
- Systematic problem-solving: Employing methodical approaches like differencing, subsequence analysis, and modulo arithmetic is critical in exploring potential patterns.
- Critical thinking: It's important to recognize the limitations of different approaches and avoid overfitting.
- Considering alternative interpretations: The possibility of encoded information or random data reminds us to think beyond purely mathematical interpretations.
- The crucial role of context: The lack of a clear answer highlights the need for additional information to solve ambiguous problems.
The sequence, in its ambiguity, serves as a potent reminder of the challenges and rewards inherent in pattern recognition. It encourages creative thinking, rigorous mathematical exploration, and a mindful awareness of the limitations of our analytical tools. Ultimately, understanding this sequence requires not just mathematical prowess but also a keen sense of context and a willingness to explore multiple possibilities.
Latest Posts
Latest Posts
-
Can You Buy Cold Sandwiches With Food Stamps At Wawa
Jul 29, 2025
-
How Many Squares In A Pallet Of Shingles
Jul 29, 2025
-
How Long Is A 40 Mile Drive
Jul 29, 2025
-
Which Is Larger 2 3 Or 3 4
Jul 29, 2025
-
Is Shelby Lynne Related To Loretta Lynn
Jul 29, 2025
Related Post
Thank you for visiting our website which covers about 8 6 9 5 10 4 11 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.