8 Is What Percent Of 2
Kalali
Apr 06, 2025 · 5 min read
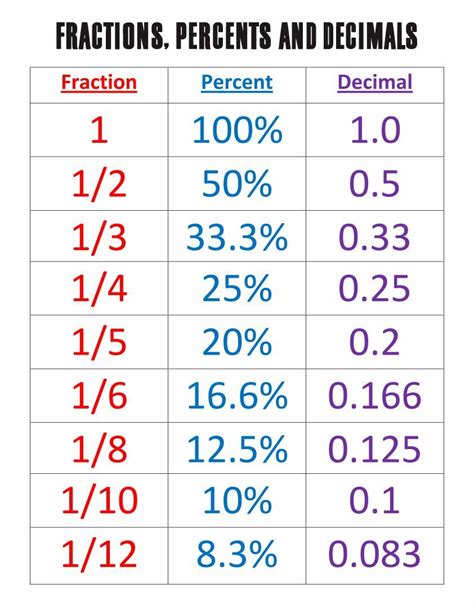
Table of Contents
8 is What Percent of 2? A Deep Dive into Percentages and Their Applications
This seemingly simple question, "8 is what percent of 2?", opens the door to a surprisingly rich exploration of percentages, their calculations, and their widespread applications in various fields. While the immediate answer might seem counterintuitive, understanding the underlying principles reveals a fundamental concept in mathematics and its practical relevance. Let's delve into this fascinating topic.
Understanding Percentages: The Foundation
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred" (from the Latin per centum). It's a way to express a proportion or a part of a whole. For instance, 50% means 50 out of 100, or one-half. Understanding this basic definition is crucial to solving percentage problems, including our central question.
Key Terminology:
- Percentage: The value represented as a number followed by the "%" symbol.
- Part: The specific amount we are considering as a portion of the whole.
- Whole: The total amount or the complete quantity.
Calculating Percentages: The Formula
The core formula for calculating percentages is:
(Part / Whole) * 100% = Percentage
This formula allows us to determine the percentage that one number represents of another. Let's apply this to our initial question: "8 is what percent of 2?"
Applying the Formula to "8 is What Percent of 2?"
In this case:
- Part = 8
- Whole = 2
Substituting these values into the formula:
(8 / 2) * 100% = 400%
Therefore, 8 is 400% of 2.
Why the Result Might Seem Unexpected
The result of 400% might seem counterintuitive at first glance. Many people instinctively associate percentages with values between 0% and 100%. However, percentages can and often do exceed 100%. This occurs when the "part" is larger than the "whole". In our example, 8 is significantly larger than 2, resulting in a percentage greater than 100%.
Think of it this way: if you have 2 apples and then acquire 8 apples, you now have 4 times the initial amount (8/2 = 4). Expressing this as a percentage, we get 400%.
Real-World Applications of Percentages Exceeding 100%
Percentages exceeding 100% are common in various real-world scenarios. Here are some examples:
- Business and Finance: A company's revenue might increase by 150% compared to the previous year, indicating a substantial growth exceeding the initial value. Similarly, stock prices often experience percentage increases that far surpass 100%.
- Population Growth: When a town's population increases significantly, it can be expressed as a percentage exceeding 100% compared to its previous population.
- Scientific Measurements: In scientific experiments and data analysis, percentage increases exceeding 100% can signify substantial changes or variations in measurements.
- Investment Returns: Investors often celebrate returns that surpass 100%, marking a doubling or tripling of their initial investment.
Beyond the Basic Calculation: Understanding the Context
The simple calculation provides the numerical answer. However, understanding the context is equally important. The question "8 is what percent of 2?" could arise in various scenarios with different interpretations. For example:
-
Scenario 1: Profit Margin Imagine a business with initial investment capital of 2 units and a profit of 8 units. The 400% represents a phenomenal return on investment. The percentage highlights the profitability and success of the venture.
-
Scenario 2: Population Increase Consider a village whose population increases from 200 to 800 individuals. Applying the calculation in this context, we'd first reduce the values to their base units: 2 and 8. Thus, the population increase is 400%, representing significant growth in the community.
-
Scenario 3: Measurement Error Suppose a laboratory experiment requires a precise measurement of 2 units. Due to an error, the measurement shows 8 units. The 400% illustrates a significant measurement error that needs to be addressed.
Understanding the specific context of the problem is key to interpreting the percentage result meaningfully.
Alternative Methods for Calculating Percentages
While the formula (Part / Whole) * 100% is the most straightforward approach, other methods can be used, particularly if working with fractions or decimals:
-
Using Fractions: Convert the part and whole into a fraction, then multiply by 100%. For our example: 8/2 = 4; 4 * 100% = 400%.
-
Using Proportions: Set up a proportion: x/100 = 8/2. Solving for 'x' will give you the percentage.
-
Using a Calculator: Most calculators have a percentage function that simplifies the calculation.
Expanding Your Understanding: Percentage Change and Increase/Decrease
Related to the basic percentage calculation is the concept of percentage change. This measures the relative change between an initial value and a final value. The formula is:
[(Final Value - Initial Value) / Initial Value] * 100% = Percentage Change
This is used frequently to calculate:
- Percentage Increase: When the final value is greater than the initial value.
- Percentage Decrease: When the final value is less than the initial value.
For example, if the value increases from 10 to 15:
[(15 - 10) / 10] * 100% = 50% increase
Similarly, if the value decreases from 20 to 15:
[(15 - 20) / 20] * 100% = -25% decrease (Note the negative sign indicating a decrease).
Practical Application: Solving Real-World Percentage Problems
Let's consider a few more scenarios to solidify our understanding:
Example 1: A store offers a 20% discount on a product originally priced at $50. What is the discounted price?
First, calculate the discount amount: 20% of $50 = (20/100) * $50 = $10
Then, subtract the discount from the original price: $50 - $10 = $40
The discounted price is $40.
Example 2: A student scored 45 out of 60 on a test. What is the percentage score?
(45 / 60) * 100% = 75%
The student scored 75%.
Example 3: A company's profits increased from $100,000 to $150,000. What is the percentage increase?
[(150,000 - 100,000) / 100,000] * 100% = 50%
The company's profits increased by 50%.
Conclusion: The Significance of Percentages in Everyday Life
Percentages are an integral part of our daily lives. From calculating discounts and taxes to understanding financial reports, interpreting scientific data, and comprehending statistical information, a firm grasp of percentages is invaluable. This article has not only answered the initial question but also provided a broader understanding of percentages, their calculation, their diverse applications, and how to interpret them accurately in various contexts. Remember that while the basic formula is straightforward, understanding the context is vital for drawing meaningful conclusions from percentage calculations, even when the result exceeds 100%. This knowledge empowers you to make informed decisions in a world saturated with numerical data presented in percentage form.
Latest Posts
Latest Posts
-
How Much Is 190 Celsius In Fahrenheit
Apr 07, 2025
-
What Percentage Of 6 Is 4
Apr 07, 2025
-
90 Out Of 300 As A Percentage
Apr 07, 2025
-
How To Find Time With Acceleration And Distance
Apr 07, 2025
-
1 2 Pint Equals How Many Cups
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about 8 Is What Percent Of 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.