8 Is What Percent Of 20
Kalali
Apr 01, 2025 · 5 min read
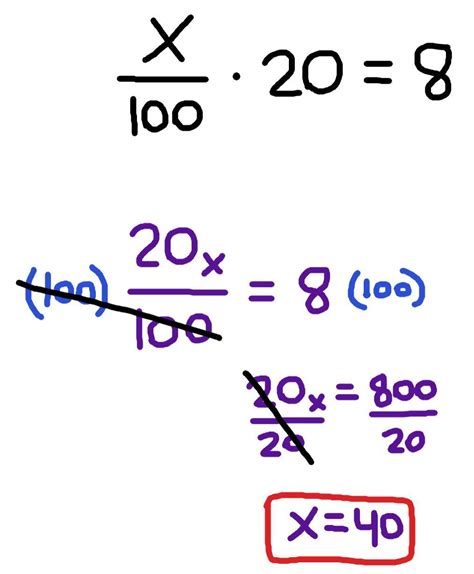
Table of Contents
8 is What Percent of 20: A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill with wide-ranging applications in everyday life, from calculating discounts and sales tax to analyzing financial data and understanding statistical information. This comprehensive guide delves into the question, "8 is what percent of 20?", providing not only the answer but also a detailed explanation of the underlying mathematical principles and various methods for solving similar percentage problems. We'll explore different approaches, including using proportions, decimals, and the formula method, ensuring you develop a thorough understanding of percentage calculations.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of 100" (per centum in Latin). Therefore, 10% means 10 out of 100, which can be written as the fraction 10/100 or the decimal 0.10. Understanding this fundamental concept is crucial to tackling percentage problems effectively.
Method 1: Using Proportions
Proportions are an excellent way to solve percentage problems. A proportion is a statement that two ratios are equal. In the context of our problem, "8 is what percent of 20?", we can set up a proportion as follows:
8/20 = x/100
Where:
- 8 represents the part.
- 20 represents the whole.
- x represents the unknown percentage.
- 100 represents the total percentage (100%).
To solve for x, we cross-multiply:
20x = 800
Then, divide both sides by 20:
x = 40
Therefore, 8 is 40% of 20.
This method is particularly useful for visualizing the relationship between the part and the whole and is easily adaptable to various percentage problems.
Method 2: Using Decimals
This method involves converting the fraction representing the part to a decimal and then multiplying by 100 to express it as a percentage.
First, express the relationship as a fraction:
8/20
Next, simplify the fraction by dividing the numerator (8) by the denominator (20):
8 ÷ 20 = 0.4
Finally, multiply the decimal by 100 to convert it to a percentage:
0.4 × 100 = 40%
This approach is straightforward and efficient, especially when working with simpler fractions.
Method 3: Using the Formula Method
The formula method offers a more direct approach to solving percentage problems. The basic formula is:
(Part / Whole) × 100 = Percentage
In our case:
(8 / 20) × 100 = 40%
This formula encapsulates the essence of percentage calculations, offering a concise and easily memorable solution.
Practical Applications of Percentage Calculations
The ability to calculate percentages is essential in numerous real-world scenarios:
1. Financial Calculations:
- Calculating discounts: If a store offers a 20% discount on a $50 item, you can quickly determine the discount amount and the final price using percentage calculations.
- Determining sales tax: Understanding how to calculate sales tax is vital for budgeting and managing personal finances.
- Analyzing investments: Percentages are crucial for understanding investment returns, growth rates, and assessing the performance of different investment options.
- Understanding interest rates: Whether it's a savings account, loan, or credit card, comprehending interest rates involves percentage calculations.
2. Data Analysis and Statistics:
- Interpreting statistical data: Percentages are frequently used in statistical reports to represent proportions and trends. Understanding percentages is crucial for making informed decisions based on this data.
- Calculating percentages of change: Determining the percentage increase or decrease in sales, population, or other variables is a common application of percentage calculations.
3. Everyday Life:
- Calculating tips: Determining the appropriate tip amount in restaurants or for services rendered involves percentage calculations.
- Understanding nutritional information: Nutritional labels often use percentages to express the proportion of daily recommended values for various nutrients.
Solving More Complex Percentage Problems
The methods discussed above can be readily applied to more complex percentage problems. For example:
- Finding the whole when given the part and the percentage: If 25% of a number is 15, what is the number?
- Finding the part when given the whole and the percentage: What is 30% of 80?
- Calculating percentage increase or decrease: A price increased from $10 to $15. What is the percentage increase?
By applying the same principles of proportions, decimals, or the formula method, these more complex problems can be solved effectively. The key lies in carefully identifying the 'part', the 'whole', and the known percentage, and then using the appropriate method to solve for the unknown value.
Advanced Percentage Concepts
For those seeking a deeper understanding of percentages, exploring advanced concepts can further enhance your mathematical skills:
- Compound interest: Understanding how interest accumulates over time, considering both principal and accumulated interest.
- Percentage points: Differentiating between percentage change and percentage points, which are often confused.
- Weighted averages: Calculating averages where different values have different weights or importance.
Mastering these advanced concepts allows for a more nuanced understanding of percentage calculations and their applications in various fields.
Conclusion: Mastering Percentage Calculations
This comprehensive guide has explored the question, "8 is what percent of 20?" in detail, providing various methods for solving this type of percentage problem. We've not only provided the answer (40%) but also explained the underlying mathematical principles and demonstrated how these principles can be applied to a wide range of practical situations. By understanding the fundamental concepts of percentages and practicing the different methods presented, you'll be well-equipped to tackle any percentage calculation you encounter, empowering you to make informed decisions in various aspects of life. Remember to practice regularly and apply these methods to real-world problems to solidify your understanding and build confidence in your percentage calculation abilities. This will undoubtedly enhance your problem-solving skills and open doors to a more comprehensive understanding of quantitative data.
Latest Posts
Latest Posts
-
How Does A Simple Machine Make Work Easier
Apr 02, 2025
-
How Many Centimeters Are In 42 Inches
Apr 02, 2025
-
Adding Integers With The Same Sign
Apr 02, 2025
-
5 To The Power Of 1
Apr 02, 2025
-
How Many Centimeters Are In 8 Feet
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about 8 Is What Percent Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
