8 Out Of 30 As A Percentage
Kalali
Apr 25, 2025 · 6 min read
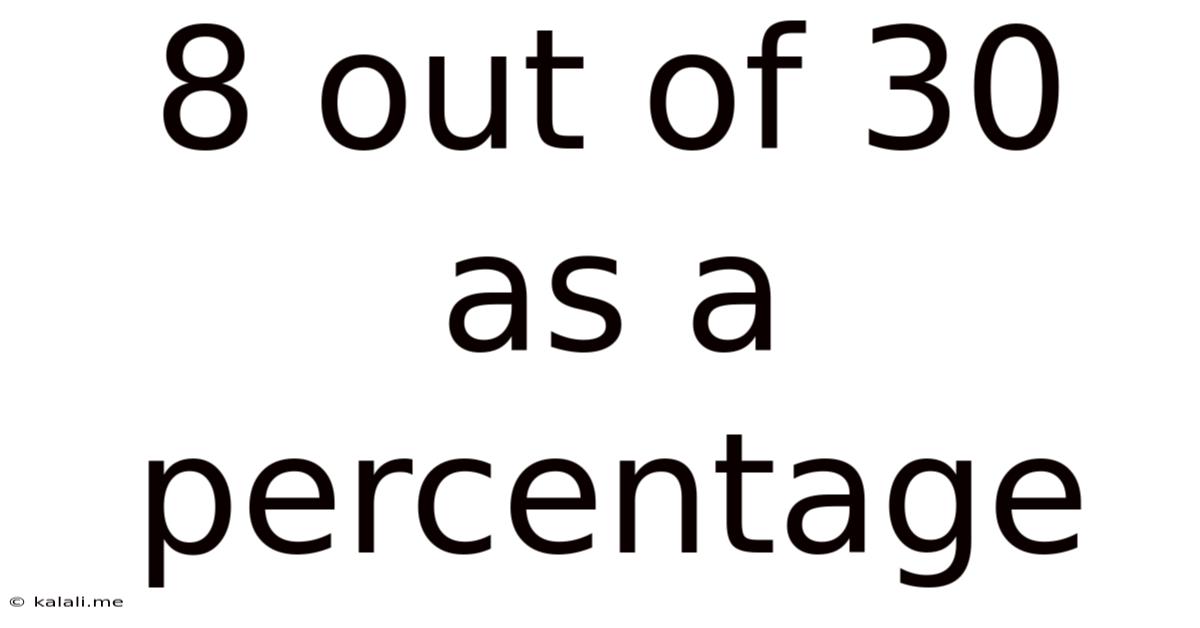
Table of Contents
8 Out of 30 as a Percentage: A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across various aspects of life, from calculating discounts and taxes to analyzing data and understanding statistics. This comprehensive guide delves into how to calculate 8 out of 30 as a percentage, providing various methods and exploring related concepts to solidify your understanding of percentage calculations. This will cover the basic method, alternative approaches, practical applications, and common mistakes to avoid. We'll also touch upon the importance of percentage calculations in different fields.
Meta Description: Learn how to calculate 8 out of 30 as a percentage. This comprehensive guide covers various methods, practical applications, and common mistakes to avoid, making percentage calculations easy to understand.
The Basic Method: Converting Fractions to Percentages
The most straightforward way to determine what percentage 8 out of 30 represents is by converting the fraction 8/30 into a percentage. Here's the step-by-step process:
-
Express the values as a fraction: The problem "8 out of 30" is already expressed as a fraction: 8/30.
-
Convert the fraction to a decimal: Divide the numerator (8) by the denominator (30): 8 ÷ 30 = 0.266666... (This decimal is recurring).
-
Convert the decimal to a percentage: Multiply the decimal by 100: 0.266666... × 100 = 26.67% (rounded to two decimal places).
Therefore, 8 out of 30 is 26.67%.
Alternative Methods: Different Approaches to the Same Solution
While the above method is the most common, several alternative approaches can achieve the same result. These alternative methods can be useful depending on the context and your preferred calculation style.
-
Simplifying the Fraction: Before converting to a decimal, simplifying the fraction can make the calculation easier. Both 8 and 30 are divisible by 2, resulting in the simplified fraction 4/15. Dividing 4 by 15 gives approximately 0.2667, which, when multiplied by 100, yields 26.67%. This method reduces the complexity of the division, especially helpful when dealing with larger numbers.
-
Using Proportions: You can set up a proportion to solve this problem. The proportion would be: 8/30 = x/100, where 'x' represents the percentage. Cross-multiplying gives 30x = 800. Solving for 'x' (divide both sides by 30) yields x ≈ 26.67.
-
Using a Calculator: Most calculators have a percentage function. Simply input 8 ÷ 30 and then multiply the result by 100 to obtain the percentage. This is the quickest and most efficient method for most people, particularly when dealing with more complex calculations.
Practical Applications: Real-World Scenarios Involving Percentages
Understanding percentage calculations is vital in various real-world situations. Here are some examples where calculating 8 out of 30, or similar percentage calculations, might be useful:
-
Academic Performance: If a student answered 8 out of 30 questions correctly on a test, their score would be 26.67%. This helps assess their understanding of the subject matter.
-
Sales and Marketing: If a company sold 8 out of 30 units of a particular product, their sales conversion rate for that product would be 26.67%. This information is critical for evaluating marketing campaigns and inventory management.
-
Data Analysis: In statistical analysis, percentages are frequently used to represent proportions or ratios within a data set. For example, if a survey of 30 people found that 8 preferred a specific brand, this represents a 26.67% preference rate.
-
Financial Calculations: Percentages are integral to calculating interest rates, returns on investments, discounts, taxes, and many other financial aspects. For instance, if you receive 8 points out of 30 possible points on a credit score check, this can impact your eligibility for a loan.
-
Quality Control: In manufacturing, the percentage of defective products is crucial for quality control. If 8 out of 30 products are found to be defective, this represents a 26.67% defect rate, signaling the need for process improvement.
Common Mistakes to Avoid When Calculating Percentages
Even simple percentage calculations can lead to errors if precautions are not taken. Here are some common mistakes to watch out for:
-
Incorrect Order of Operations: Always ensure you perform the division before multiplying by 100. Dividing 100 by 30 first and then multiplying by 8 will yield an incorrect result.
-
Rounding Errors: Rounding too early in the calculation process can lead to inaccuracies in the final result. It's best to round only at the very end, ideally to an appropriate number of decimal places based on the context (e.g., two decimal places for percentages).
-
Confusing Percentages with Decimals: Remember that a percentage is a fraction expressed as a hundredth. A decimal must be multiplied by 100 to be converted to a percentage.
-
Misunderstanding the Context: Always pay close attention to what the numbers represent. Ensure that you are applying the percentage calculation to the correct quantities. For instance, if you're comparing sales data for different products, ensure that you're comparing the correct values.
-
Lack of Units: Always include the percent symbol (%) when expressing a result as a percentage. This prevents confusion and clarifies the meaning of the number.
Beyond the Basics: Further Exploration of Percentage Concepts
While calculating 8 out of 30 as a percentage is a relatively straightforward calculation, understanding percentages extends beyond this simple example. Here are some related concepts to explore:
-
Percentage Increase and Decrease: Understanding how to calculate percentage increases and decreases is essential for analyzing changes over time. For example, you might want to determine the percentage increase in sales from one year to the next or the percentage decrease in unemployment.
-
Percentage Points: This is a subtle but important distinction. Percentage points refer to the absolute difference between two percentages. For example, if unemployment falls from 10% to 8%, it has decreased by 2 percentage points, not 20%.
-
Compound Interest: Compound interest involves earning interest on both the principal amount and accumulated interest. This concept is fundamental in financial planning and investment.
-
Statistical Significance: In statistical analysis, percentages are used to represent probabilities and to assess the significance of results. Understanding statistical significance is crucial for interpreting data accurately.
-
Advanced Percentage Applications: More advanced applications of percentages include calculating weighted averages, determining percentiles, and utilizing percentages in various statistical distributions.
Conclusion: Mastering Percentage Calculations
Mastering percentage calculations is a crucial skill with wide-ranging applications in various fields. This guide has provided a detailed explanation of how to calculate 8 out of 30 as a percentage, along with various alternative methods, practical applications, and common pitfalls to avoid. By understanding these concepts and practicing regularly, you can confidently tackle percentage calculations in any situation, fostering a strong foundation for more complex mathematical applications. Remember to always double-check your work and ensure that your calculations are accurate and relevant to the context. The ability to confidently calculate and interpret percentages will greatly enhance your analytical skills and decision-making abilities.
Latest Posts
Latest Posts
-
What Is The Decimal For 5 12
Apr 25, 2025
-
What Color Has The Longest Wavelength
Apr 25, 2025
-
How Many Millimeters Are There In One Meter
Apr 25, 2025
-
How Many Liters In A 5 Gallon Bucket
Apr 25, 2025
-
How Many Tenths Are In A Mile
Apr 25, 2025
Related Post
Thank you for visiting our website which covers about 8 Out Of 30 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.