9 1 8 As A Decimal
Kalali
Mar 25, 2025 · 5 min read
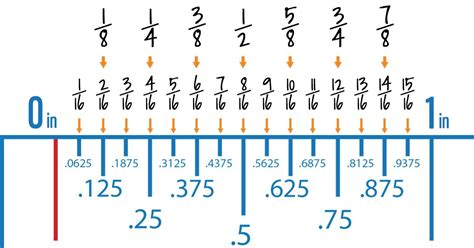
Table of Contents
9/18 as a Decimal: A Comprehensive Guide
Converting fractions to decimals is a fundamental skill in mathematics with applications spanning numerous fields, from finance and engineering to everyday calculations. This comprehensive guide dives deep into the conversion of the fraction 9/18 to its decimal equivalent, exploring various methods and highlighting crucial concepts along the way. We'll also touch upon the broader implications of decimal representation and its significance in practical applications.
Understanding Fractions and Decimals
Before we delve into the specific conversion of 9/18, let's briefly review the fundamental concepts of fractions and decimals.
A fraction represents a part of a whole. It consists of two parts: the numerator (the top number) and the denominator (the bottom number). The numerator indicates the number of parts we have, while the denominator indicates the total number of equal parts the whole is divided into.
A decimal is a way of writing a number that is not a whole number. It uses a decimal point to separate the whole number part from the fractional part. The digits to the right of the decimal point represent tenths, hundredths, thousandths, and so on.
Simplifying the Fraction 9/18
The first step in converting 9/18 to a decimal is to simplify the fraction. Simplifying a fraction means reducing it to its lowest terms by finding the greatest common divisor (GCD) of the numerator and the denominator and dividing both by it.
In this case, both 9 and 18 are divisible by 9. Therefore:
9 ÷ 9 = 1 18 ÷ 9 = 2
This simplifies the fraction 9/18 to 1/2. Simplifying the fraction before conversion makes the subsequent steps significantly easier and less prone to errors.
Method 1: Long Division
The most straightforward method to convert a fraction to a decimal is through long division. We divide the numerator (1) by the denominator (2):
0.5
2 | 1.0
1.0
---
0
Therefore, 1/2 (and consequently 9/18) is equal to 0.5.
Step-by-Step Long Division Explanation:
-
Set up the division: Write the numerator (1) inside the division symbol and the denominator (2) outside. Add a decimal point and a zero after the 1 to make it 1.0.
-
Divide: Ask yourself, "How many times does 2 go into 1?" It doesn't go in at all, so we write a 0 above the 1.
-
Bring down the zero: Bring down the 0 from the 1.0 to make 10.
-
Divide again: Ask yourself, "How many times does 2 go into 10?" It goes in 5 times. Write a 5 above the 0.
-
Subtract: Multiply 5 by 2 (which is 10) and subtract it from 10. The result is 0. This indicates that the division is complete.
Method 2: Using Equivalent Fractions
Another approach involves converting the fraction to an equivalent fraction with a denominator that is a power of 10 (10, 100, 1000, etc.). This method is particularly useful when the denominator is a factor of a power of 10.
Since the simplified fraction is 1/2, we can multiply both the numerator and denominator by 5 to obtain an equivalent fraction with a denominator of 10:
(1 x 5) / (2 x 5) = 5/10
5/10 can be easily written as a decimal: 0.5.
Method 3: Using a Calculator
The simplest method, albeit less insightful in terms of mathematical understanding, is using a calculator. Simply enter 9 ÷ 18 (or 1 ÷ 2 after simplification) and the calculator will display the decimal equivalent: 0.5.
Understanding the Decimal Representation: 0.5
The decimal 0.5 represents one-half (1/2) or fifty hundredths (50/100). It signifies a value exactly halfway between 0 and 1 on the number line. Its simplicity and common usage make it a frequently encountered decimal in various calculations.
Applications of Decimal Conversion
The ability to convert fractions to decimals is crucial in various applications:
-
Finance: Calculating percentages, interest rates, and proportions in financial transactions heavily relies on decimal representation.
-
Engineering and Science: Precise measurements and calculations in engineering and scientific fields necessitate the accurate conversion between fractions and decimals.
-
Cooking and Baking: Following recipes often requires converting fractional measurements into decimal equivalents for greater precision.
-
Everyday Life: Many everyday situations require the conversion of fractions to decimals, such as splitting bills, calculating discounts, and measuring quantities.
Further Exploration: Recurring Decimals
While 9/18 results in a terminating decimal (0.5), it's important to note that not all fractions convert to terminating decimals. Some fractions result in recurring decimals, where one or more digits repeat infinitely. For example, 1/3 converts to 0.333... where the 3 repeats infinitely. Understanding the distinction between terminating and recurring decimals is essential for a comprehensive grasp of decimal representation.
Conclusion: Mastering Fraction to Decimal Conversion
Converting fractions like 9/18 to decimals is a fundamental mathematical skill with practical implications across various disciplines. Through understanding the underlying concepts and employing different methods—long division, equivalent fractions, or a calculator—one can confidently navigate this essential conversion process. Mastering this skill enhances numerical literacy and problem-solving abilities, paving the way for more complex mathematical challenges and applications in the real world. The simplicity of 9/18's decimal equivalent, 0.5, serves as a clear illustration of these principles and provides a solid foundation for tackling more complex fractional conversions. Remember to always simplify fractions first to make the conversion process smoother and more efficient.
Latest Posts
Latest Posts
-
What Is 3 2 In A Decimal
Mar 28, 2025
-
200 M Is How Many Feet
Mar 28, 2025
-
How Many Ounces In 34 Pounds
Mar 28, 2025
-
How Do You Graph Tangent Functions
Mar 28, 2025
-
What Is 15 Percent Of 300
Mar 28, 2025
Related Post
Thank you for visiting our website which covers about 9 1 8 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
