9 Out Of 50 As A Percentage
Kalali
Apr 13, 2025 · 5 min read
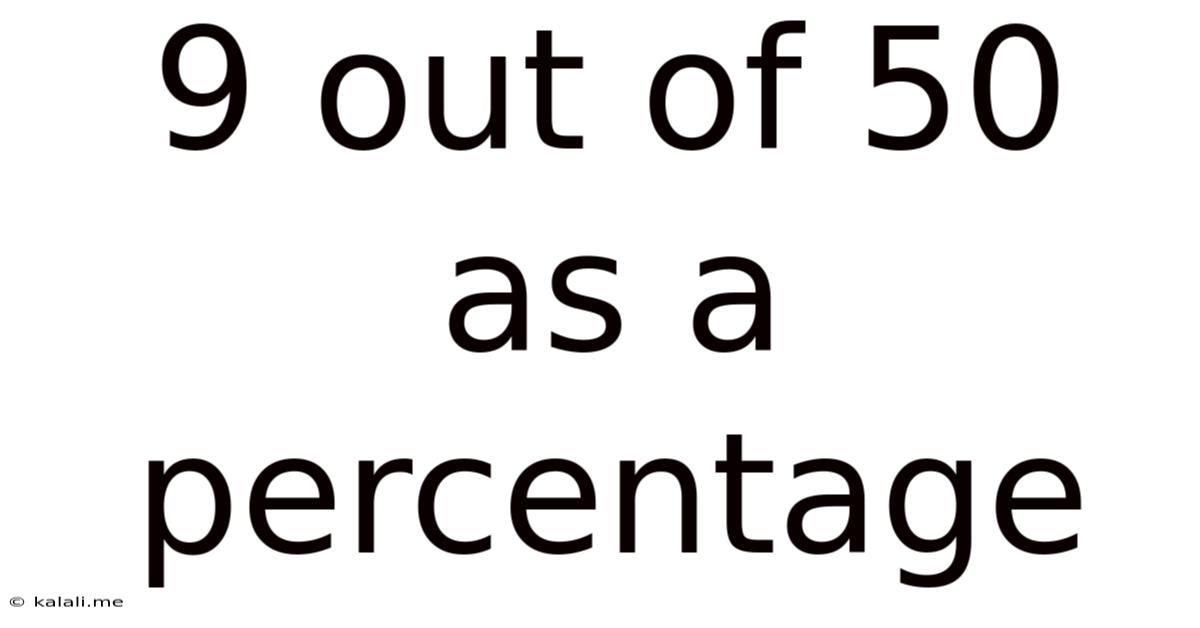
Table of Contents
9 Out of 50 as a Percentage: A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in numerous aspects of life, from calculating discounts and taxes to analyzing data and understanding statistics. This article delves into the specifics of calculating "9 out of 50 as a percentage," providing a step-by-step guide, various calculation methods, and practical applications. We'll also explore related concepts and offer tips for mastering percentage calculations. This comprehensive guide will ensure you confidently handle percentage problems in any context.
Meta Description: Learn how to calculate 9 out of 50 as a percentage. This detailed guide covers different calculation methods, practical applications, and related percentage concepts, ensuring you master percentage calculations.
Understanding the Basics of Percentages
Before we dive into the specific calculation, let's refresh our understanding of percentages. A percentage is simply a fraction out of 100. The term "percent" comes from the Latin "per centum," meaning "out of a hundred." Therefore, 25% means 25 out of 100, which can also be expressed as the fraction 25/100 or the decimal 0.25.
Percentages are used to express proportions or ratios. They're invaluable for comparing different quantities, representing changes over time, and making data more accessible and understandable. For example, in a sales context, a 10% discount is easily understood compared to saying "1/10 off."
Method 1: Using the Fraction Method to Calculate 9 out of 50 as a Percentage
This is the most straightforward method. We convert the given ratio ("9 out of 50") into a fraction and then convert that fraction into a percentage.
-
Express the ratio as a fraction: 9 out of 50 can be written as the fraction 9/50.
-
Convert the fraction to a percentage: To express a fraction as a percentage, we multiply it by 100%. This is because a percentage is a fraction with a denominator of 100.
(9/50) * 100% = 18%
Therefore, 9 out of 50 is equal to 18%.
Method 2: Using Decimal Conversion to Calculate 9 out of 50 as a Percentage
This method involves first converting the fraction to a decimal and then converting the decimal to a percentage.
-
Convert the ratio to a decimal: Divide the numerator (9) by the denominator (50): 9 ÷ 50 = 0.18
-
Convert the decimal to a percentage: Multiply the decimal by 100%: 0.18 * 100% = 18%
Again, we arrive at the same answer: 9 out of 50 is 18%.
Method 3: Using Proportions to Calculate 9 out of 50 as a Percentage
This method utilizes the concept of proportions, which is particularly useful when dealing with more complex percentage problems.
We set up a proportion where one ratio represents the given numbers (9 out of 50) and the other ratio represents the unknown percentage (x out of 100):
9/50 = x/100
To solve for x, we cross-multiply:
9 * 100 = 50 * x
900 = 50x
x = 900/50
x = 18
Therefore, x = 18%, confirming that 9 out of 50 is 18%.
Practical Applications of Percentage Calculations
Understanding how to calculate percentages is crucial in a wide range of real-world situations. Here are a few examples:
-
Sales and Discounts: Calculating discounts, sales tax, and final prices after discounts. For instance, if an item is 20% off, you need to calculate the discount amount and the final price.
-
Finance and Investing: Calculating interest rates, returns on investments, and understanding financial statements. For example, calculating compound interest requires a thorough understanding of percentage calculations.
-
Statistics and Data Analysis: Representing data as percentages makes it easier to understand and compare different quantities. For instance, analyzing survey results often involves converting raw numbers into percentages.
-
Everyday Life: Calculating tips, splitting bills, and understanding tax rates all involve percentage calculations.
-
Science and Engineering: Percentages are widely used in scientific research, engineering calculations, and data representation. For example, expressing experimental error or efficiency rates.
Beyond the Basics: More Complex Percentage Problems
While calculating 9 out of 50 is relatively straightforward, other percentage problems might require more intricate calculations. For example:
-
Finding the original value: If an item is discounted by 20% and costs $80, what was the original price? This involves working backward from the discounted price to find the original value.
-
Calculating percentage change: Determining the percentage increase or decrease between two values. This is commonly used to track changes in sales, stock prices, or populations.
-
Compounding percentages: Calculating the effect of multiple percentage changes applied sequentially. This is important in finance, where interest might compound annually or monthly.
Tips for Mastering Percentage Calculations
-
Practice regularly: The more you practice, the more comfortable you'll become with different types of percentage problems.
-
Use different methods: Try all three methods described above to find the one that best suits your understanding and the specific problem.
-
Break down complex problems: Divide complex percentage problems into smaller, more manageable steps.
-
Check your work: Always double-check your calculations to ensure accuracy.
-
Use online calculators (for verification): While not a substitute for understanding the methods, online percentage calculators can be useful for checking your answers.
Conclusion
Calculating 9 out of 50 as a percentage, which equals 18%, is a fundamental skill with widespread applications. Mastering percentage calculations empowers you to confidently tackle various numerical problems in everyday life, finance, and professional settings. By understanding the basic principles and practicing different calculation methods, you can build a solid foundation for handling even more complex percentage problems. Remember to focus on the underlying concepts, practice regularly, and utilize different methods to solidify your understanding. With consistent effort, mastering percentages will become second nature.
Latest Posts
Latest Posts
-
19 Is What Percent Of 76
Apr 15, 2025
-
The Following Sequence Has Terms That Decrease Exponentially
Apr 15, 2025
-
Cuantos Grados Centigrados Son 41 Fahrenheit
Apr 15, 2025
-
What Is 135 Out Of 150
Apr 15, 2025
-
Do All Transition Metals Have 2 Valence Electrons
Apr 15, 2025
Related Post
Thank you for visiting our website which covers about 9 Out Of 50 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.