19 Is What Percent Of 76
Kalali
Apr 15, 2025 · 5 min read
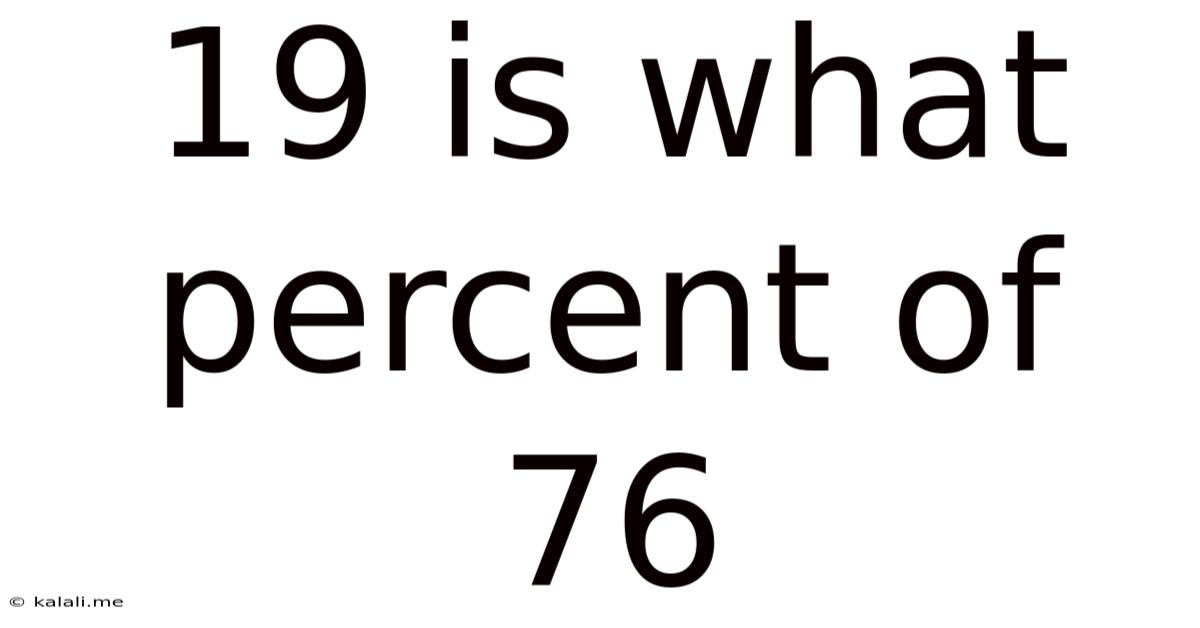
Table of Contents
19 is What Percent of 76? A Comprehensive Guide to Percentage Calculations
This article will thoroughly explore the question: "19 is what percent of 76?" We'll delve into the solution, explain the underlying mathematical principles, provide alternative methods for solving similar problems, and explore practical applications of percentage calculations in various fields. Understanding percentages is crucial for numerous aspects of daily life, from financial planning and budgeting to analyzing data and interpreting statistics. This guide aims to equip you with the knowledge and tools to confidently tackle percentage problems.
Meta Description: Learn how to calculate percentages with a detailed explanation of how to solve "19 is what percent of 76?". This guide covers various methods, real-world applications, and helpful tips for mastering percentage calculations.
Understanding the Fundamentals of Percentages
Before diving into the specific problem, let's solidify our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "percent," meaning "out of one hundred." For example, 50% means 50 out of 100, which is equivalent to 50/100 or 1/2.
Percentages are used extensively to represent proportions, rates, and changes. They are particularly useful for comparing different quantities or expressing parts of a whole. For instance, we might say that 25% of a class scored above 90% on a test, or that the price of a product has increased by 10%.
Solving "19 is What Percent of 76?"
The core of the problem lies in setting up a proportion. We want to find the percentage (x) that represents 19 out of 76. We can represent this relationship as a fraction:
19/76 = x/100
To solve for x, we can cross-multiply:
19 * 100 = 76 * x
1900 = 76x
Now, we isolate x by dividing both sides of the equation by 76:
x = 1900 / 76
x = 25
Therefore, 19 is 25% of 76.
Alternative Methods for Calculating Percentages
While the proportion method is straightforward, several other methods can be used to solve percentage problems. These alternative methods can be helpful depending on the specific problem and your preferred approach.
Method 1: Using Decimal Conversion
We can convert the fraction 19/76 into a decimal by performing the division:
19 ÷ 76 = 0.25
To convert this decimal to a percentage, we multiply by 100:
0.25 * 100 = 25%
This method is particularly useful when working with a calculator.
Method 2: Using the Percentage Formula
The basic percentage formula is:
(Part / Whole) * 100 = Percentage
In our problem:
Part = 19 Whole = 76
(19 / 76) * 100 = 25%
This formula provides a clear and concise way to structure the calculation.
Practical Applications of Percentage Calculations
Understanding percentages is essential in many aspects of life. Here are some examples:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns. Understanding percentage changes helps in analyzing financial performance and making informed investment decisions. For example, calculating the percentage increase in your savings account balance or the percentage decrease in the price of a stock.
-
Retail: Determining discounts on sale items, calculating sales tax, and comparing prices from different retailers. This understanding is crucial for savvy shopping and maximizing your purchasing power.
-
Science: Expressing experimental results, statistical data analysis, and calculating error margins. Percentages are essential for presenting and interpreting scientific findings accurately and effectively.
-
Education: Calculating grades, assessing student performance, and analyzing test scores. This facilitates the evaluation of learning outcomes and the overall effectiveness of teaching methods.
-
Health: Interpreting health statistics, tracking progress in fitness goals, and understanding medication dosages. Percentages provide a clear way to represent the prevalence of diseases, the effectiveness of treatments, and individual health metrics.
-
Data Analysis: Representing proportions within datasets, calculating changes over time, and interpreting survey results. This is important for drawing accurate conclusions and making informed decisions based on data-driven insights.
Advanced Percentage Calculations: Percentage Increase and Decrease
Beyond basic percentage calculations, understanding percentage increases and decreases is crucial. Let's explore these concepts:
Percentage Increase: This represents the relative increase in a quantity. The formula is:
[(New Value - Original Value) / Original Value] * 100 = Percentage Increase
For example, if the price of an item increases from $50 to $60, the percentage increase is:
[(60 - 50) / 50] * 100 = 20%
Percentage Decrease: This represents the relative decrease in a quantity. The formula is:
[(Original Value - New Value) / Original Value] * 100 = Percentage Decrease
For example, if the price of an item decreases from $60 to $48, the percentage decrease is:
[(60 - 48) / 60] * 100 = 20%
Troubleshooting and Common Mistakes
When working with percentages, it's easy to make mistakes. Here are some common errors to avoid:
-
Incorrectly identifying the "part" and the "whole": Always ensure you are correctly identifying the values in your problem. The "whole" is the total amount, while the "part" is the portion you are interested in.
-
Misplacing the decimal point: Be careful when converting between decimals and percentages. Remember to multiply by 100 when converting decimals to percentages and divide by 100 when converting percentages to decimals.
-
Rounding errors: When rounding numbers, make sure you are rounding correctly to avoid significant errors, especially in complex calculations. Consider using more decimal places during intermediate steps to minimize rounding errors.
-
Not using the correct formula: Choose the appropriate formula for your specific percentage problem, be it calculating a percentage of a number, finding a percentage increase or decrease, or solving a more complex problem involving multiple percentages.
Conclusion: Mastering Percentage Calculations
This article provided a comprehensive guide to understanding and solving percentage problems, specifically addressing the question "19 is what percent of 76?" We explored various calculation methods, highlighted practical applications across diverse fields, and discussed common pitfalls to avoid. By mastering these concepts and techniques, you'll be better equipped to tackle percentage problems confidently and effectively in your daily life, academic pursuits, and professional endeavors. Remember to practice regularly to solidify your understanding and improve your calculation speed and accuracy. The more you practice, the easier percentage calculations will become.
Latest Posts
Latest Posts
-
20 Is What Percent Of 10
Apr 16, 2025
-
How Much Is 220 Celsius In Fahrenheit
Apr 16, 2025
-
How Many Milliliters Are In 1 Fluid Ounce
Apr 16, 2025
-
45 Is What Percent Of 60
Apr 16, 2025
-
List The Main Properties Of Metals
Apr 16, 2025
Related Post
Thank you for visiting our website which covers about 19 Is What Percent Of 76 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.