A 2 X 2 1 2 Integral
Kalali
May 24, 2025 · 3 min read
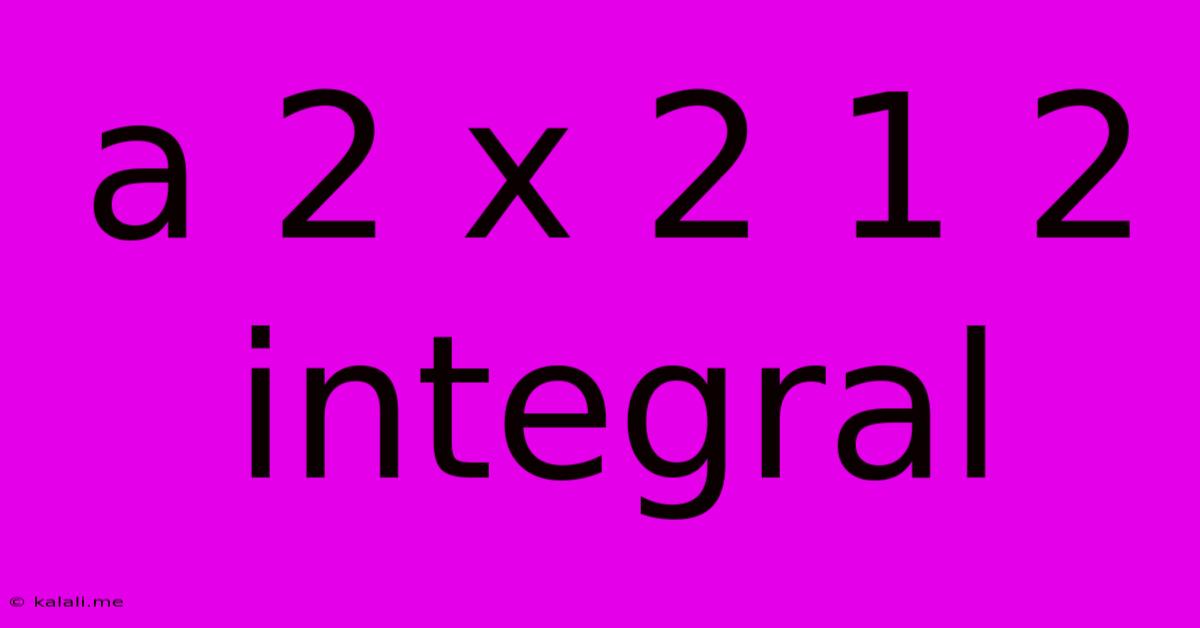
Table of Contents
Decoding the 2 x 2 x 1/2 Integral: A Comprehensive Guide
This article delves into the intricacies of evaluating a 2 x 2 x 1/2 integral, a seemingly simple yet potentially complex problem depending on the integrand. We'll explore different approaches, highlighting common pitfalls and offering strategies for a successful solution. Understanding this type of integral is crucial for various fields, including physics, engineering, and advanced mathematics.
What does a "2 x 2 x 1/2 integral" actually mean?
The notation "2 x 2 x 1/2 integral" isn't standard mathematical terminology. It likely refers to a triple integral over a region defined by three limits of integration, where two of the limits might be constants (2 and 2), and one might be a fraction or a function (1/2). The actual meaning depends entirely on the specific integrand and the limits of integration. To illustrate, let's consider several scenarios:
Scenario 1: A Simple Case
Let's assume the integral is of the form:
∫∫∫<sub>R</sub> f(x,y,z) dx dy dz
where R is defined by 0 ≤ x ≤ 2, 0 ≤ y ≤ 2, and 0 ≤ z ≤ 1/2. In this case, the integral represents the volume integral of the function f(x,y,z) over a rectangular prism with dimensions 2 x 2 x 1/2. The solution method is straightforward:
- Iterated Integration: We evaluate the integral iteratively, starting with the innermost integral (dz), followed by dy, and finally dx.
- Order of Integration: The order of integration can significantly impact the complexity of the calculation. Choosing the optimal order often involves inspecting the integrand to identify potential simplifications.
- Fundamental Theorem of Calculus: We apply the fundamental theorem of calculus to evaluate each integral with respect to its variable.
Scenario 2: Introducing Complexity
Consider a scenario where the limits of integration are functions of other variables: 0 ≤ x ≤ 2, 0 ≤ y ≤ 2, and 0 ≤ z ≤ x/2. Now, the region R is no longer a simple rectangular prism. It becomes a more complex three-dimensional shape, requiring a careful consideration of the integration bounds.
Scenario 3: Dealing with Difficult Integrands
Even with simple integration limits, the complexity can arise from a challenging integrand. For example, integrating a function with trigonometric functions, exponentials, or special functions necessitates advanced integration techniques such as:
- Substitution: Changing variables to simplify the integrand.
- Integration by Parts: Using the product rule for derivatives in reverse.
- Partial Fraction Decomposition: Breaking down rational functions into simpler fractions.
Strategies for Solving 2 x 2 x 1/2 Integrals (and beyond):
- Visualize the Region: Sketching the region of integration is essential for understanding the bounds and choosing the optimal order of integration.
- Simplify the Integrand: Look for opportunities to simplify the integrand before attempting integration. This might involve algebraic manipulation, trigonometric identities, or other simplification techniques.
- Change of Variables: In some cases, a change of variables (such as cylindrical or spherical coordinates) can significantly simplify the integral.
- Numerical Methods: If analytical integration proves difficult or impossible, numerical integration methods (e.g., Simpson's rule, Gaussian quadrature) can provide an approximate solution.
Conclusion:
The term "2 x 2 x 1/2 integral" lacks precise mathematical definition. However, the principles discussed here apply broadly to triple integrals. Understanding the region of integration, carefully selecting the integration order, and employing appropriate integration techniques are crucial for successfully solving these problems. Remember to always visualize the integration region and simplify the integrand as much as possible to avoid common pitfalls. When confronted with an intractable integral, numerical methods are a valuable tool.
Latest Posts
Latest Posts
-
Net Register Service From Aonther Assembly
May 25, 2025
-
Bash Can A Variable Be Assigned Indirectly
May 25, 2025
-
Why Kattappa Killed Bahubali Because Of Bhallaladeva
May 25, 2025
-
What Kind Of Weapon Disables Robot
May 25, 2025
-
Wordpress Htaccess Redirect With Path In Tact
May 25, 2025
Related Post
Thank you for visiting our website which covers about A 2 X 2 1 2 Integral . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.