A Parallelogram With Four Right Angles
Kalali
Apr 07, 2025 · 6 min read
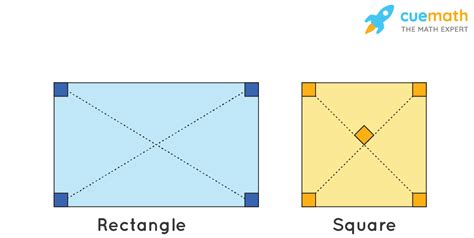
Table of Contents
A Parallelogram with Four Right Angles: Exploring the Properties of a Rectangle
A parallelogram is a fundamental geometric shape defined by its parallel sides. However, when we add the constraint of four right angles, we transition from the general parallelogram to a specific and incredibly useful type: the rectangle. This article delves into the fascinating world of rectangles, exploring their properties, theorems, applications, and the unique relationship they hold within the broader family of quadrilaterals. We'll examine their characteristics, delve into proofs of key properties, and showcase real-world examples highlighting their significance.
Defining the Rectangle: More Than Just a Parallelogram
A rectangle is defined as a parallelogram with four right angles. This seemingly simple addition fundamentally alters the shape's characteristics. While all rectangles are parallelograms, not all parallelograms are rectangles. This distinction is crucial for understanding the hierarchy of quadrilaterals.
Let's break down the key properties inherent in the definition:
- Parallelogram: This implies two pairs of parallel sides. Opposite sides are equal in length.
- Four Right Angles: Each interior angle measures exactly 90 degrees.
These two properties intertwine to create a shape with remarkable symmetry and predictable properties.
Key Properties of Rectangles
The defining properties of a rectangle lead to a cascade of additional characteristics:
1. Opposite Sides are Equal and Parallel
This property is inherited directly from the parallelogram definition. Let's denote the sides of the rectangle as AB, BC, CD, and DA. Then:
- AB || CD and AB = CD
- BC || DA and BC = DA
This parallelism and equality are fundamental to many applications of rectangles.
2. All Angles are Right Angles
This is the defining characteristic differentiating a rectangle from a general parallelogram. The four right angles create the distinct rectangular shape. This 90-degree angle at each vertex is crucial for calculating areas, diagonals, and solving geometric problems involving rectangles.
3. Diagonals are Equal and Bisect Each Other
This is a unique property of rectangles. Let's denote the diagonals as AC and BD. Then:
- AC = BD
- AC and BD bisect each other (they intersect at their midpoints).
This property is easily proven using the Pythagorean theorem and congruent triangles.
Proof: Consider triangles ABC and BAD. AB is a common side. BC = AD (opposite sides of a rectangle are equal), and angles ABC and BAD are both right angles. Therefore, triangles ABC and BAD are congruent by the Side-Angle-Side (SAS) congruence theorem. This congruence implies that AC = BD (corresponding parts of congruent triangles are congruent). Similarly, it can be shown that the diagonals bisect each other.
4. Area Calculation: A Simple Formula
The area of a rectangle is exceptionally straightforward to calculate:
Area = length × width
Where length and width represent the lengths of adjacent sides. This formula's simplicity underpins its wide use in various fields, from architecture and engineering to everyday tasks like calculating the area of a room or a piece of land.
5. Perimeter Calculation: The Sum of All Sides
Calculating the perimeter (the total distance around the rectangle) is equally straightforward:
Perimeter = 2 × (length + width)
This formula is crucial in numerous applications, including determining the amount of fencing needed for a rectangular yard or the length of trim required for a rectangular frame.
Rectangles and Other Quadrilaterals: A Hierarchical Relationship
Rectangles occupy a specific place within the broader family of quadrilaterals. The hierarchy can be visualized as follows:
- Quadrilaterals: Four-sided polygons.
- Parallelograms: Quadrilaterals with two pairs of parallel sides.
- Rectangles: Parallelograms with four right angles.
- Squares: Rectangles with four equal sides.
This hierarchy demonstrates that a square is a special case of a rectangle, which in turn is a special case of a parallelogram, and ultimately a quadrilateral. Understanding this hierarchy is crucial for grasping the relationships between different geometric shapes.
Theorems and Proofs Related to Rectangles
Many theorems in geometry are directly related to or rely on the properties of rectangles. Here are a few examples:
-
The Pythagorean Theorem: This fundamental theorem is often used in conjunction with rectangles to solve problems involving diagonal lengths and side lengths. The theorem states that in a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
-
Congruence Theorems: As demonstrated earlier, congruence theorems (like SAS and SSS) are frequently employed to prove properties of rectangles, such as the equality of diagonals.
-
Similar Rectangles: Two rectangles are similar if their corresponding angles are congruent and their corresponding sides are proportional. This concept is crucial in scaling and resizing rectangular objects.
Real-World Applications of Rectangles
Rectangles are ubiquitous in the world around us. Their simple yet powerful properties make them exceptionally useful in a vast array of applications:
-
Architecture and Construction: Buildings, rooms, windows, and doors are often rectangular, due to the ease of construction and efficient use of space.
-
Engineering: Rectangular shapes are commonly used in structural design, due to their strength and stability. Many bridges, beams, and frameworks incorporate rectangular elements.
-
Packaging and Manufacturing: Boxes, containers, and many manufactured goods often utilize rectangular shapes for efficient packing, shipping, and storage.
-
Art and Design: Rectangles form the basis of many artistic compositions, providing a stable and pleasing visual framework.
-
Everyday Objects: Screens, tables, books, and countless other everyday objects are rectangular in shape.
Advanced Concepts and Extensions
While we've covered the fundamental aspects of rectangles, there are advanced concepts worth exploring:
-
Rectangular Coordinates: The Cartesian coordinate system, based on perpendicular x and y axes, is fundamentally rectangular in nature. This system is crucial in various branches of mathematics, physics, and computer graphics.
-
Rectangular Matrices: In linear algebra, rectangular matrices (matrices with different numbers of rows and columns) play a significant role in various computations and transformations.
-
Higher Dimensional Analogues: The concept of a rectangle can be extended to higher dimensions. For instance, a three-dimensional analogue would be a rectangular prism (or cuboid).
Conclusion: The Enduring Importance of Rectangles
The rectangle, a seemingly simple shape, holds a position of profound importance in mathematics, science, engineering, and everyday life. Its predictable properties, ease of calculation, and wide-ranging applications make it a cornerstone of geometric understanding and a fundamental building block in countless real-world structures and designs. From the intricate designs of skyscrapers to the simple act of measuring a room, the rectangle's influence is undeniable, demonstrating the power of seemingly simple geometric concepts. Its inherent properties and their mathematical proofs continue to inspire and challenge mathematicians and other scientists alike, cementing its place as a foundational shape in our understanding of the world around us.
Latest Posts
Latest Posts
-
Cuanto Es 108 Grados Fahrenheit En Centigrados
Apr 09, 2025
-
Explain The Significance Of Crossing Over
Apr 09, 2025
-
How Many Quarts In 3 Gallons
Apr 09, 2025
-
How Big Is 48 Inches In Feet
Apr 09, 2025
-
What Percentage Is 6 Out Of 7
Apr 09, 2025
Related Post
Thank you for visiting our website which covers about A Parallelogram With Four Right Angles . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.