A Ray That Divides An Angle Into 2 Congruent Angles
Kalali
Mar 30, 2025 · 6 min read
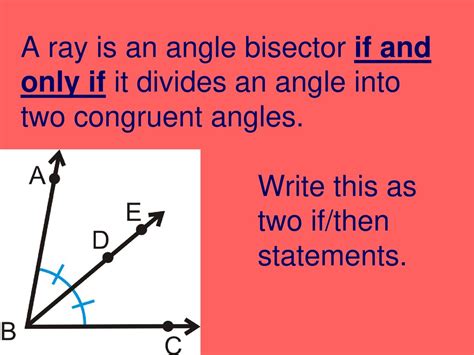
Table of Contents
A Ray That Divides an Angle into Two Congruent Angles: Exploring Angle Bisectors
The concept of an angle bisector is fundamental in geometry, forming the cornerstone of many geometric proofs and constructions. Understanding its properties and applications is crucial for mastering various geometrical concepts. This comprehensive guide delves deep into the definition, properties, construction, and applications of an angle bisector, providing a solid foundation for anyone studying geometry.
Defining an Angle Bisector
An angle bisector is a ray that originates from the vertex of an angle and divides the angle into two congruent angles. In simpler terms, it's a line segment or ray that cuts an angle precisely in half. Crucially, the two newly formed angles are not only equal in measure but also are considered congruent—meaning they have the same size and shape. This seemingly simple concept underlies numerous geometric theorems and problem-solving techniques.
Consider an angle ∠ABC. If ray BD bisects ∠ABC, then ∠ABD ≅ ∠DBC, and m∠ABD = m∠DBC = (m∠ABC)/2. The notation "≅" denotes congruence, while "m∠" represents the measure of the angle.
Key Terminology Clarification
Understanding the terminology is crucial. Let's clarify some key terms:
- Angle: A figure formed by two rays that share a common endpoint (the vertex).
- Ray: A part of a line that has one endpoint and extends infinitely in one direction.
- Vertex: The common endpoint of two rays that form an angle.
- Congruent Angles: Angles that have the same measure.
- Bisect: To divide into two equal parts.
Properties of Angle Bisectors
Angle bisectors possess several essential properties that make them valuable tools in geometry. These properties allow us to deduce relationships and solve problems involving angles and triangles.
Property 1: Equality of the Two Resulting Angles
The most fundamental property is the one we've already discussed: an angle bisector divides an angle into two congruent angles. This forms the basis for many proofs and constructions.
Property 2: Unique Angle Bisector
For any given angle, there exists only one angle bisector. This uniqueness is a crucial property, meaning that you cannot have two distinct rays bisecting the same angle. This unique bisector is defined by the ray that divides the angle precisely in half.
Property 3: Application in Triangles – Angle Bisector Theorem
The angle bisector theorem states that within a triangle, the angle bisector of an angle divides the opposite side into segments that are proportional to the lengths of the other two sides. Let's consider a triangle ABC, with an angle bisector AD from vertex A to side BC. The theorem states that AB/AC = BD/DC. This property proves incredibly useful in solving problems involving triangles and ratios.
Constructing an Angle Bisector
Constructing an angle bisector involves using a compass and straightedge. The process is straightforward and is a fundamental skill in geometry. Here's a step-by-step guide:
-
Start with the angle: Begin with the angle you wish to bisect. Label the vertex as point A, and the two rays as AB and AC.
-
Draw arcs: Place the compass point on vertex A. Draw an arc that intersects both rays AB and AC. Label these intersection points as D and E, respectively. Ensure that the compass radius is large enough for the arcs to intersect.
-
Draw intersecting arcs: Without changing the compass radius, place the compass point on D. Draw an arc in the interior of the angle. Then, keeping the same compass radius, place the compass point on E and draw another arc that intersects the first arc. Label the intersection point of these arcs as F.
-
Draw the bisector: Draw a ray from vertex A passing through point F. This ray, AF, is the angle bisector. It precisely divides ∠BAC into two congruent angles: ∠BAF and ∠CAF.
This construction method relies on the properties of circles and congruent triangles, demonstrating a powerful application of basic geometric principles.
Applications of Angle Bisectors
Angle bisectors have numerous applications within mathematics and beyond. Understanding their properties unlocks various problem-solving techniques and provides insights into complex geometrical relationships.
1. Solving Geometric Problems
Angle bisectors are essential in solving a wide range of geometric problems. They allow us to determine unknown angles, side lengths, and other geometric properties within various shapes like triangles, quadrilaterals, and more complex polygons. Many geometry problems require the use of angle bisectors to find solutions.
2. Incenter of a Triangle
The intersection point of the three angle bisectors of a triangle is known as the incenter. This point is equidistant from the three sides of the triangle and is the center of the inscribed circle (incircle) of the triangle. The incircle is the largest circle that can be drawn inside the triangle, touching all three sides.
3. Geometric Constructions
As illustrated in the construction method, angle bisectors are fundamental in creating various geometric figures with precise measurements. Many geometrical constructions rely on the ability to bisect angles accurately.
4. Computer Graphics and Design
The concept of angle bisectors is vital in computer-aided design (CAD) and computer graphics. It is used in creating symmetrical shapes, generating patterns, and implementing transformations in digital design.
5. Architecture and Engineering
Angle bisectors have practical applications in architecture and engineering. Symmetrical designs, structural integrity assessments, and accurate measurements often involve employing the properties of angle bisectors.
6. Navigation and Surveying
Understanding angles and their bisections is crucial for navigation and surveying applications. Accurate angle measurements and their division are used in determining directions and mapping terrain.
Advanced Concepts Related to Angle Bisectors
For those seeking a deeper understanding, several advanced concepts build upon the foundations of angle bisectors:
-
Exterior Angle Bisectors: While we've focused on interior angle bisectors, exterior angle bisectors also exist. These rays bisect the angles formed by extending one side of the angle. They exhibit similar properties but in the context of exterior angles.
-
Angle Trisectors: These rays divide an angle into three congruent angles. Constructing angle trisectors is more complex than bisecting angles but is another area of exploration in geometry.
-
Applications in Trigonometry: Angle bisectors find applications in trigonometry, aiding in the solution of triangles using trigonometric functions.
Conclusion: The Power of Precision
The seemingly simple concept of an angle bisector reveals a profound power in geometrical problem-solving. Understanding its definition, properties, and construction methods provides a strong foundation for tackling complex geometric problems. From its applications in solving geometric problems to its essential role in various fields, the angle bisector remains a crucial concept in geometry and beyond. Its precise nature ensures accuracy in construction, design, and various real-world applications, highlighting its continued relevance in mathematics and various disciplines. The study of angle bisectors allows for a deeper understanding of geometric relationships and enhances problem-solving abilities within the realm of geometry and beyond.
Latest Posts
Latest Posts
-
What Is The Least Common Multiple Of 5 And 12
Apr 01, 2025
-
2 5 Ounces Is How Many Ml
Apr 01, 2025
-
Why Does Passive Transport Not Require Energy
Apr 01, 2025
-
What Is 65 As A Fraction
Apr 01, 2025
-
How Many Miles Is 1600 Km
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about A Ray That Divides An Angle Into 2 Congruent Angles . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
